द्रव गतिविज्ञान: Difference between revisions
(d bvhvhtbbv) |
No edit summary |
||
| (47 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Aspects of fluid mechanics involving flow}} | {{Short description|Aspects of fluid mechanics involving flow}} | ||
[[File:Teardrop shape.svg|thumb|300px|विशिष्ट [[:hi:वायुगतिकी|वायुगतिकीय]] अश्रु आकार, बाएं से दाएं गुजरने वाले एक [[:hi:श्यानता|चिपचिपा]] माध्यम मानते हुए, आरेख दबाव वितरण को काली रेखा की मोटाई के रूप में दिखाता है और [[:hi:परिसीमा स्तर|सीमा परत]] में वेग को वायलेट त्रिकोण के रूप में दिखाता है। हरे [[:hi:भंवर जनरेटर|भंवर जनरेटर]] [[:hi:प्रक्षुब्ध प्रवाह|अशांत प्रवाह]] के लिए संक्रमण को प्रेरित करते हैं और बैक-फ्लो को रोकते हैं जिसे पीठ में उच्च दबाव वाले क्षेत्र से [[:hi:प्रवाह पृथक्करण|प्रवाह पृथक्करण]] भी कहा जाता है। सामने की सतह यथासंभव चिकनी है या यहां तक कि [[:hi:त्वचीय दांत|शार्क जैसी त्वचा]] का भी उपयोग करती है, क्योंकि यहां कोई भी अशांति वायु प्रवाह की ऊर्जा को बढ़ाती है। दाईं ओर का कटाव, जिसे [[:hi:स्पॉयलर (वैमानिकी)|कम्बैक]] के रूप में जाना जाता है, स्पॉइलर के पीछे के उच्च दबाव वाले क्षेत्र से अभिसरण भाग में [[:hi:कम्बैक|बैकफ़्लो]] को रोकता है। ]]'''द्रव गतिकी,''' [[भौतिकी]] तथा [[इंजीनियरिंग|अभियान्त्रिकी]] में [[द्रव यांत्रिकी]] का उपविषय है, जिसके अंतर्गत [[तरल पदार्थ-तरल|तरल पदार्थों]] एवं [[गैसों]] के प्रवाह का अध्ययन किया जाता है। इसमें ''वायुगतिकी'' (गति में वायु तथा अन्य गैसों का अध्ययन) तथा '''हाइड्रोडायनामिक्स''' (गति में तरल पदार्थों का अध्ययन) सहित कई उप-विषय हैं। द्रव गतिकी में, [[विमान]] पर [[बलों|बल]] तथा [[क्षणों|आघुर्ण]] की गणना करना, [[पाइपलाइनों]] के माध्यम से [[पेट्रोलियम]] के [[द्रव्यमान प्रवाह दर]] का निर्धारण, [[मौसम के पैटर्न की भविष्यवाणी करना|मौसम का पूर्वानुमान लगाना]], [https://en.wikipedia.org/wiki/Outer_space#Interstellar_space|'''अंतर्तारकीय क्षेत्र'''] में [[नेबुला]] को समझना एवं [https://en.wikipedia.org/wiki/Nuclear_weapon_design|'''विखंडन हथियार विस्फोट का प्रतिरूपण'''] जैसे अनुप्रयोगों कि एक विस्तृत श्रृंखला शामिल है। | |||
[[File:Teardrop shape.svg|thumb|300px|विशिष्ट | |||
द्रव गतिकी | द्रव गतिकी [[व्यावहारिक विषयों|प्रयोगात्मक विषयों]] कि एक व्यवस्थित संरचना प्रदान करती है। जो [[प्रवाह माप]] से प्राप्त प्रयोगाश्रित एवं अर्ध-प्रयोगाश्रित नियमो का पालन करती है तथा प्रयोगात्मक समस्याओं को हल करने के लिए उपयोग की जाती है। द्रव गतिकी समस्या के हल के लिए प्राय: द्रव के विभिन्न गुणों जैसे कि स्थान तथा समय के फलन के रूप में, [[प्रवाह वेग]], [[दबाव|दाब]], [[घनत्व]] तथा [[तापमान]] की गणना शामिल होती है। | ||
बीसवीं शताब्दी से पहले, ''हाइड्रोडायनामिक्स'' द्रव गतिकी का पर्याय था। यह अभी भी कुछ द्रव गतिकी विषयों | बीसवीं शताब्दी से पहले, ''हाइड्रोडायनामिक्स'' द्रव गतिकी का पर्याय था। यह अभी भी कुछ द्रव गतिकी विषयों जैसे [[मैग्नेटोहाइड्रोडायनामिक्स]] तथा [[हाइड्रोडायनामिक स्थिरता]] के नामों मे परिलक्षित होता है, जो दोनों को गैसों पर भी लागू किया जा सकता है।<ref>{{Cite book|title=The Dawn of Fluid Dynamics: A Discipline Between Science and Technology|first=Michael|last=Eckert|publisher=Wiley|year=2006|isbn=3-527-40513-5|page=ix}}</ref> | ||
== समीकरण == | == समीकरण == | ||
द्रव गतिकी | द्रव गतिकी मे [[शास्त्रीय यांत्रिकी|चिरसम्मत यांत्रिकी]] पर आधारित, [[द्रव्यमान का संरक्षण]], [[रेखीये संवेग का संरक्षण]], तथा [[ऊर्जा संरक्षण|ऊर्जा का संरक्षण]] (जिसे [[थर्मोडायनामिक्स का पहला नियम|उष्मागतिकी का पहला नियम]] भी कहा जाता है) जैसे मूलभूत स्वयंसिद्ध [[संरक्षण नियम]] हैं। जिन्हे [[क्वांटम यांत्रिकी]] तथा [[सामान्य सापेक्षता]] में संशोधित किया गया हैं। वे [[रेनॉल्ड्स परिवहन प्रमेय|रेनॉल्ड्स आवेग प्रमेय]] का उपयोग करके व्यक्त किए जाते हैं। | ||
उपरोक्त के अलावा, | उपरोक्त के अलावा, तरल पदार्थ अणुओं से बने होते हैं जो एक दूसरे से तथा ठोस वस्तुओं से टकराते हैं तथा [[सातत्य धारणा]] का पालन करते हैं। हालांकि, सातत्य धारणा के अनुसार तरल पदार्थ असतत के बजाय सतत होते हैं, जिसके परिणामस्वरूप, अंतरिक्ष में [[असीम रूप]] से छोटे बिंदुओं पर घनत्व, दाब, तापमान तथा प्रवाह वेग जैसे गुण अच्छी तरह से परिभाषित होते हैं तथा एक बिंदु से दूसरे बिंदु पर लगातार भिन्न होते हैं। | ||
तरल पदार्थ | तरल पदार्थ जो सातत्य होने के लिए पर्याप्त रूप से सघन होते हैं, जिनमें आयनिक प्रजातियां नहीं होती हैं तथा प्रकाश की गति के संबंध में प्रवाह वेग छोटा होता है, [[नेवियर-स्टोक्स समीकरण]] [[अवकल समीकरणों]] का [[अरैखिक]] समुच्चय है, जो [[न्यूटोनियन तरल पदार्थों]] के लिए गति समीकरण होता है तथा तरल पदार्थ के प्रवाह का वर्णन करता है, जिसका तनाव प्रवाह वेग ढाल तथा दाब पर रैखिक रूप से निर्भर करता है। सरलीकृत समीकरणों में एक सामान्य [[बंद-रूप समाधान|संवृत रूप हल]] नहीं होता है, इसलिए वे मुख्य रूप से [[कम्प्यूटेशनल तरल गतिकी|संगणनात्मक तरल गतिकी]] में उपयोग किए जाते हैं। समीकरणों को कई तरीकों से हल किया जा सकता है। कुछ सरलीकरण कुछ सरल द्रव गतिकी समस्याओं को संवृत रूप में हल करने की अनुमति देते हैं। | ||
द्रव्यमान, संवेग | द्रव्यमान, संवेग तथा ऊर्जा संरक्षण समीकरणों के अलावा, समस्या के पूर्ण वर्णन के लिए, [[थर्मोडायनामिक|ऊष्मागतिकी]] अवस्था समीकरण जिसमे दाब अन्य ऊष्मागतिकी चर का फलन होता है, की आवश्यकता होती है। इसका एक उदाहरण [[राज्य का आदर्श गैस समीकरण|आदर्श गैस का अवस्था समीकरण]] है। | ||
<math>p= \frac{\rho R_u T}{M}</math> | |||
जहां p [[ | जहां p [[दबाव|दाब]], ρ [[घनत्व]], T [[पूर्ण तापमान]], R<sub>u</sub> [[गैस स्थिरांक]] तथा M एक विशेष गैस के लिए [[दाढ़ द्रव्यमान|मोलर द्रव्यमान]] है। | ||
===संरक्षण | ===संरक्षण नियम === | ||
द्रव गतिकी समस्याओं को हल करने के लिए तीन संरक्षण | द्रव गतिकी समस्याओं को हल करने के लिए तीन संरक्षण नियमो का उपयोग किया जाता है, जिन्हे [[अभिन्न|समाकल]] या [[विभेदक|अवकल]] रूप में लिखा जाता है। संरक्षण नियम प्रवाह के क्षेत्र पर लागू किया जा सकता है जिसे ''नियंत्रण खंड'' कहा जाता है। नियंत्रित आयतन अंतरिक्ष में असतत आयतन है जिसके माध्यम से द्रव प्रवाहित होता है। नियंत्रित आयतन मे द्रव्यमान, गति या ऊर्जा के परिवर्तन का वर्णन संरक्षण नियमो के समाकल सूत्रीकरण के द्वार किया जाता है। संरक्षण नियमो के अवकल सूत्रीकरण एक समतुल्य संबंध उत्पन्न करने के लिए [[स्टोक्स के प्रमेय]] को लागू किया जाता है, जिसे प्रवाह में एक असीम रूप से छोटी मात्रा (एक बिंदु पर) पर लागू नियम के समाकल रूप के रूप में व्यखित किया जा सकता है। | ||
यद्यपि ऊर्जा को एक रूप से दूसरे रूप में परिवर्तित किया जा सकता है, एक बंद | ==== [[द्रव्यमान सातत्य]] (द्रव्यमान का संरक्षण) ==== | ||
नियंत्रित आयतन मे द्रव द्रव्यमान के परिवर्तन की दर आयतन में द्रव प्रवाह की नेट दर के बराबर होनी चाहिए। भौतिक रूप से, नियंत्रित आयतन में द्रव्यमान न तो उत्पन्न किया जा सकता है और न ही नष्ट किया जा सकता है, और इसका सांतत्य समीकरण का समाकल रूप प्रदर्शित किया गया है। | |||
: <math>\frac{\partial}{\partial t} \iiint_V \rho \, dV = - \, {} </math> {{oiint|preintegral = |intsubscpt =<math>{\scriptstyle S}</math>|integrand = <math>{}\,\rho\mathbf{u}\cdot d\mathbf{S}</math>}} | |||
उपरोक्त समीकरण मे <math>{\displaystyle {\displaystyle \rho}}</math> द्रव घनत्व ह, u [[प्रवाह वेग]] सदिश तथा t समय है। उपरोक्त समीकरण के बाएं हाथ की मात्रा मे द्रव्यमान की वृद्धि की दर तथा नियंत्रित आयतन पर एक त्रि-समकालन है, जबकि दायीं ओर निकाय मे संवहित द्रव्यमान के नियंत्रित आयतन की सम्पूर्ण सतह के लिए समकालन है। निकाय मे द्रव्यमान प्रवाह को सकारात्मक माना जाता है, [[अपसरण प्रमेय]] द्वारा सातत्य समीकरण का अवकल रूप नीचे दिए गए समीकरण द्वारा प्रदर्शित किया जा सकता है। | |||
<math>{\displaystyle \ {\frac {\partial \rho }{\partial t}}+\nabla \cdot (\rho \mathbf {u} )=0}</math> | |||
==== [[गति का संरक्षण]] ==== | |||
[[न्यूटन की गति का दूसरा नियम|न्यूटन के गति का दूसरा नियम]] नियंत्रित आयतन पर लागू होता है, यह एक कथन है कि नियंत्रित आयतन मे द्रव के संवेग में कोई भी परिवर्तन आयतन में संवेग के शुद्ध प्रवाह तथा आयतन मे द्रव पर कार्य करने वाले बाहरी बलों की क्रिया के कारण होता है। | |||
<math>{\displaystyle {\frac {\partial }{\partial t}}\iiint _{\scriptstyle V}\rho \mathbf {u} \,dV=-\,{}} | |||
{\displaystyle _{\scriptstyle S}} | |||
{\displaystyle (\rho \mathbf {u} \cdot d\mathbf {S} )\mathbf {u} -{}} | |||
{\displaystyle {\scriptstyle S}} | |||
{\displaystyle {}\,p\,d\mathbf {S} } | |||
{\displaystyle \displaystyle {}+\iiint _{\scriptstyle V}\rho \mathbf {f} _{\text{body}}\,dV+\mathbf {F} _{\text{surf}}} | |||
</math> | |||
इस समीकरण के उपरोक्त समाकल सूत्रीकरण में, बाईं ओर का पद मात्रा में संवेग का नेट परिवर्तन है। दायीं ओर का पहला पद नेट दर है जिस पर संवेग आयतन में संवहित होता है और दूसरा पद आयतन की सतहों पर दाब के कारण लगने वाला बल है। निकाय में प्रवेश करने वाले संवेग के धनात्मक होने के कारण दायीं ओर के पहले दो पदों को अस्वीकार कर दिया जाता है, और सामान्य वेग u और दाब बलों की दिशा के विपरीत होता है। दायीं ओर का तीसरा पद किसी भी [[पिंड बल]] (यहाँ f<sub>body</sub> द्वारा दर्शाया गया है) के कारण आयतन मे द्रव्यमान का नेट त्वरण है। [[सतही बल]], जैसे श्यान बल, F<sub>surf</sub> द्वारा दर्शाए जाते हैं, जो आयतन सतह पर कार्य करने वाले [[अपरूपण बलों]] के कारण नेट बल होता है। संवेग संतुलन को गतिमान नियंत्रित आयतन के लिए भी लिखा जा सकता है। संवेग संरक्षण समीकरण का अवकल रूप निम्नलिखित है। यहां आयतन को एक छोटे से छोटे बिंदु तक कम कर दिया जाता है, और सतह और पिंड की शक्ति दोनों को कुल बल '''F''' के लिए जिम्मेदार बताया जाता है। उदाहरण के लिए, प्रवाह में '''F''' को एक बिंदु पर अभिनय करने वाले घर्षण और गुरुत्वाकर्षण बलों के लिए एक अभिव्यक्ति में विस्तारित किया जा सकता है। | |||
<math>{\displaystyle \ {\frac {D\mathbf {u} }{Dt}}=\mathbf {F} -{\frac {\nabla p}{\rho }}}</math> | |||
[[वायुगतिकी]] में, हवा को [[न्यूटोनियन द्रव]] माना जाता है, जो अपरूपण तनाव (आंतरिक घर्षण बलों के कारण) तथा द्रव के तनाव की दर के बीच एक रैखिक संबंध रखता है। उपरोक्त समीकरण त्रि-विमीय प्रवाह में एक सदिश समीकरण है, लेकिन इसे तीन समन्वित दिशाओं में तीन अदिश समीकरणों के रूप में व्यक्त किया जा सकता है। संपीड़ित, श्यान प्रवाह के लिए संवेग संरक्षण के समीकरणों को नेवियर-स्टोक्स समीकरण कहा जाता है। | |||
==== [[ऊर्जा का संरक्षण]] ==== | |||
यद्यपि ऊर्जा को एक रूप से दूसरे रूप में परिवर्तित किया जा सकता है, एक संवृत (बंद) निकाय में कुल ऊर्जा स्थिर रहती है। | |||
: <math>\ \rho \frac{Dh}{Dt} = \frac{D p}{D t} + \nabla \cdot \left( k \nabla T\right) + \Phi </math> | : <math>\ \rho \frac{Dh}{Dt} = \frac{D p}{D t} + \nabla \cdot \left( k \nabla T\right) + \Phi </math> | ||
विशिष्ट | उपरोक्त समीकरण मे ''h'' विशिष्ट एन्थैल्पी है, {{mvar|k}} द्रव की तापीय चालकता है, {{mvar|T}} तापमान और {{mvar|Φ}} श्यान अपव्यय फलन है, बाईं ओर का व्यंजक भौतिक व्युत्पन्न है। श्यान अपव्यय फलन उस दर को नियंत्रित करता है, जिस पर प्रवाह की यांत्रिक ऊर्जा उष्मा में परिवर्तित हो जाती है। ऊष्मागतिकी के दूसरे नियम के लिए अपव्यय पद हमेशा सकारात्मक होना आवश्यक है। श्यान्ता नियंत्रित आयतन मे ऊर्जा नहीं बना सकता है।<ref>{{cite book |last=White |first=F. M. |title=Viscous Fluid Flow |location=New York |publisher=McGraw–Hill |year=1974 |isbn=0-07-069710-8 }}</ref> | ||
== वर्गीकरण == | == वर्गीकरण == | ||
===संपीड़ित | ===संपीड़ित की तुलना में असंपीड़ित प्रवाह === | ||
सभी तरल पदार्थ एक | सभी तरल पदार्थ एक सीमा तक [[संकुचित]] होते हैं, अर्थात् दाब या तापमान में परिवर्तन से घनत्व में परिवर्तन होता है। हालांकि, कई स्थितियों में दाब और तापमान में परिवर्तन इतना कम होता है कि घनत्व में बदलाव नगण्य होता है। इस स्थिति में प्रवाह को एक [[असम्पीडित प्रवाह]] के रूप में प्रतिदर्श किया जा सकता है। अन्यथा अधिक सामान्य [[संपीड़ित प्रवाह]] समीकरणों का उपयोग किया जा सकता है। | ||
गणितीय रूप से, | गणितीय रूप से, ρ को यह कहकर व्यक्त किया जाता है कि [[द्रव पार्सल]] का घनत्व प्रवाह क्षेत्र में गति करने पर नहीं बदलता है, अर्थात, | ||
: <math>\frac{\mathrm{D} \rho}{\mathrm{D}t} = 0 \, ,</math> | : <math>\frac{\mathrm{D} \rho}{\mathrm{D}t} = 0 \, ,</math> | ||
जहां पर {{math|{{sfrac|D|D''t''}}}} द्रव्यात्मक अवकलज है, जो क्षेत्रीय और संवहनी अवकलज का योग है। एक समान घनत्व के द्रव कि स्थिति में यह अतिरिक्त अवरोध नियंत्र समीकरणों को सरल बनाते है। | |||
प्रवाह की [[मच संख्या]] के मूल्यांकन द्वार गैसों के प्रवाह के लिए, संपीड़ित या असंपीड़ित द्रव गतिकी में उपयोगी को निर्धारित करते है। एक मोटे मार्गदर्शक के रूप में, लगभग 0.3 से नीचे मच संख्या पर संपीड़ित प्रभावों को अनदेखा किया जा सकता है। तरल पदार्थों के लिए, क्या असंपीड़ित धारणा वैध है, द्रव गुणों (विशेष रूप से महत्वपूर्ण दाब और तरल पदार्थ का तापमान) और प्रवाह की स्थिति (वास्तविक प्रवाह दाब कितना महत्वपूर्ण दाब बन जाता है) पर निर्भर करता है। ध्वनि तरंगें संपीड़न तरंगें होती हैं, अत: [[ध्वनिक]] समस्याओं के लिए हमेशा संपीड्यता की अनुमति की आवश्यकता होती है, क्योंकि जिनमें दाब में परिवर्तन और माध्यम के घनत्व में परिवर्तन के माध्यम से तरल पदार्थ फैलते हैं। | |||
=== न्यूटोनियन बनाम अ-न्यूटोनियन तरल पदार्थ === | |||
[[File:Flow around a wing.gif|thumb|एक एयरफ़ॉइल ]][[सुपरफ्लुइड्स|अति तरल]] को छोड़कर सभी तरल पदार्थ विरूपण के लिए कुछ प्रतिरोध रखते है अर्थात श्यान होते हैं। विभिन्न वेगों पर चलने वाले तरल पदार्थ के निकटवर्ती पार्सल एक दूसरे पर श्यान बल लगाते हैं। वेग प्रवणता को [[तनाव दर]] के रूप में संदर्भित किया जाता है, इसका विमा '''''T''''' '''<sup>−1</sup>''' है। [[आइजैक न्यूटन]] ने बताया कि [[पानी]] और [[हवा]] जैसे कई परिचित तरल पदार्थों के लिए, इन श्यान बलों के कारण [[तनाव]] रैखिक रूप से तनाव दर से संबंधित होता है। ऐसे द्रवों को [[न्यूटोनियन द्रव]] कहते हैं। न्यूटोनियन तरल पदार्थों के लिए तनाव दर से स्वतंत्र आनुपातिकता के गुणांक को द्रव की श्यानता (यह एक द्रव गुण है) कहा जाता है। | |||
=== | [[गैर-न्यूटोनियन तरल पदार्थों|अ-न्यूटोनियन तरल पदार्थों]] में अधिक जटिल, अरेखीय तनाव - खिंचाव व्यवहार होता है। [[रियोलॉजी|प्रवाहिकी]] का उप संकाय ऐसे तरल पदार्थों के तनाव - खिंचाव व्यवहार का वर्णन करता है, जिसमें [[इमल्शन|पायस]] और [[स्लरी|घोल]], कुछ [[विस्कोलेस्टिक|श्यानप्रत्यास्थ]] सामग्री जैसे [[रक्त]] और कुछ [[पॉलिमर|बहुलक]], और ''श्यान तरल पदार्थ'' जैसे [[लेटेक्स]], [[शहद]] और [[स्नेहक]] शामिल हैं। <ref>{{Cite journal|last=Wilson|first=DI|title=What is Rheology?|journal=Eye|date=February 2018|volume=32|issue=2|pages=179–183|doi=10.1038/eye.2017.267|pmid=29271417|pmc=5811736}}</ref> | ||
===अश्यान बनाम श्यान बनाम स्टोक्स प्रवाह === | |||
द्रव पार्सल की गतिशीलता का वर्णन [[न्यूटन के दूसरे नियम]] के द्वरा किया गया है। द्रव का त्वरित पार्सल जड़त्वीय प्रभावों के अधीन है। | |||
[[रेनॉल्ड्स संख्या]] एक [[आयामहीन मात्रा|विमाहीन मात्रा]] है जो श्यान प्रभावों के परिमाण की तुलना में जड़त्वीय प्रभावों के परिमाण की विशेषता है। छोटी रेनॉल्ड्स संख्या ({{Math|''Re'' ≪ 1}}) इंगित करती है कि श्यान बल जड़त्वीय बलों की तुलना में बहुत शक्तिशालि हैं। ऐसी स्थिति में, जड़त्वीय बलों की कभी-कभी उपेक्षा की जाती है, इस प्रवाह व्यवस्था को [[स्टोक्स या रेंगने वाला प्रवाह]] कहा जाता है। | |||
इसके विपरीत, उच्च रेनॉल्ड्स संख्या{{ | इसके विपरीत, उच्च रेनॉल्ड्स संख्या ({{Math|''Re'' ≫ 1}}) इंगित करती है कि श्यान (घर्षण) प्रभावों की तुलना में जड़त्वीय प्रभाव वेग क्षेत्र पर अधिक प्रभाव डालते हैं। उच्च रेनॉल्ड्स संख्या प्रवाह में, प्रवाह को प्रायः [[अदृश्य प्रवाह|अश्यान प्रवाह]] (अनुमान जिसमें श्यानता पूरी तरह से उपेक्षित होता है) के रूप में तैयार किया जाता है। श्यानता को खत्म करने से [[नेवियर-स्टोक्स समीकरणों]] को [[यूलर समीकरणों]] में सरल किया जा सकता है। यूलर समीकरणों का समाकलन अप्रत्यक्ष प्रवाह में एक धारा के साथ [[बर्नौली के समीकरण]] को उत्पन्न करता है। जब, अश्यान होने के अलावा, प्रवाह हर जगह [[अघूर्णी]] होता है, अतः बर्नौली का समीकरण हर जगह प्रवाह का पूरी तरह से वर्णन कर सकता है। इस तरह के प्रवाह को [[संभावित प्रवाह]] कहा जाता है, क्योंकि वेग क्षेत्र को स्थितिज ऊर्जा व्यंजक की [[प्रवणता]] के रूप में व्यक्त किया जा सकता है। | ||
हालांकि, ठोस सीमाओं को शामिल करने वाली समस्याओं के लिए श्यानता को शामिल करने की आवश्यकता हो सकती है। ठोस सीमाओं के पास श्यानता की उपेक्षा नहीं की जा सकती है<sub>,</sub> क्योंकि [[बिना पर्ची की स्थिति|नो-स्लिप स्थिति]] बड़े तनाव दर, [[सीमा परत]] का एक पतला क्षेत्र उत्पन्न करती है, जिसमें [[चिपचिपापन|श्यानता]] प्रभावी होता है और इस प्रकार [[भंवर]] उत्पन्न करता है। इसलिए, निकायों (जैसे पंख) पर नेट बलों की गणना करने के लिए, श्यान प्रवाह समीकरणों का उपयोग किया जाना चाहिए। अश्यान प्रवाह सिद्धांत [[ड्रैग फोर्स|संकर्ष बल]] की भविष्यवाणी करने में विफल रहता है, एक सीमा जिसे [[डी'एलेम्बर्ट के विरोधाभास के]] रूप में जाना जाता है। | |||
प्रायः इस्तेमाल किया जाने वाला मॉडल<ref>{{Cite journal|last=Platzer|first=B.|date=2006-12-01|title=Book Review: Cebeci, T. and Cousteix, J., Modeling and Computation of Boundary-Layer Flows|url=http://dx.doi.org/10.1002/zamm.200690053|journal=ZAMM|volume=86|issue=12|pages=981–982|doi=10.1002/zamm.200690053|issn=0044-2267}}</ref>, विशेष रूप से [[कम्प्यूटेशनल तरल गतिकी|संगणनात्मक तरल गतिकी]] में, दो प्रवाह मॉडल (पिंड से दूर यूलर समीकरण, और पिंड के करीब एक क्षेत्र में [[सीमा परत]] समीकरण) का उपयोग किया जाता है। मिलान [[किए गए स्पर्शोन्मुख विस्तार की विधि का]] उपयोग करके दो समाधानों का एक दूसरे के साथ मिलान किया जा सकता है। | |||
== | ==स्थिर बनाम अस्थिर प्रवाह == | ||
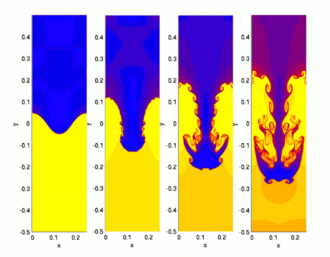
[[File:HD-Rayleigh-Taylor.gif|thumb|320px| | [[File:HD-Rayleigh-Taylor.gif|thumb|320px|रेले-टेलर अस्थिरता का हाइड्रोडायनामिक्स अनुकरण]]प्रवाह जो समय का फलन नहीं होता, '''स्थिर प्रवाह''' कहलाता है। स्थिर-अवस्था प्रवाह उस स्थिति को संदर्भित करता है जहां निकाय में एक बिंदु पर द्रव गुण समय के साथ नहीं बदलते हैं। समय पर निर्भर प्रवाह को अस्थिर (क्षणिक <ref>{{Cite web|url=https://www.cfd-online.com/Forums/main/118306-transient-state-unsteady-state.html|title=Transient state or unsteady state? -- CFD Online Discussion Forums|website=www.cfd-online.com}}</ref>) के रूप में जाना जाता है। चाहे कोई विशेष प्रवाह स्थिर हो या अस्थिर, निर्देश आधार पर निर्भर हो सकता है। उदाहरण के लिए, एक [[गोले]] के संबंध में स्थिर निर्देश आधार में गोले पर स्तरीय प्रवाह स्थिर होता है। निर्देश आधार में जो पृष्ठभूमि प्रवाह के संबंध में स्थिर है, प्रवाह अस्थिर है। | ||
[[अशांत]] प्रवाह परिभाषा के अनुसार अस्थिर हैं। हालांकि, अशांत प्रवाह [[सांख्यिकीय रूप से स्थिर]] हो सकता है। यादृच्छिक वेग क्षेत्र {{Math|''U''(''x'', ''t'')}}, यदि सभी आँकड़े समय में बदलाव के तहत अपरिवर्तनीय हो<ref name="pope2">{{Cite book|last=Pope|first=Stephen B.|title=Turbulent Flows|publisher=Cambridge University Press|year=2000|isbn=0-521-59886-9}}</ref>, सांख्यिकीय रूप से स्थिर होता हैं।<ref name="pope3">{{Cite book|last=Pope|first=Stephen B.|title=Turbulent Flows|publisher=Cambridge University Press|year=2000|isbn=0-521-59886-9}}</ref> इसका मोटे तौर पर मतलब है कि सभी सांख्यिकीय गुण समय में स्थिर हैं। प्रायः माध्य [[क्षेत्र]] रुचि का विषय होता है, और यह सांख्यिकीय रूप से स्थिर प्रवाह में भी स्थायी होता है। | |||
स्थिर प्रवाह | स्थिर प्रवाह प्रायः समान अस्थिर प्रवाह की तुलना में अधिक सुविधाजनक होते हैं। एक स्थिर समस्या के नियंत्र समीकरणों में प्रवाह क्षेत्र की स्थिरता का लाभ उठाए बिना एक ही समस्या के शासी समीकरणों की तुलना में कम आयाम (समय) होता है। | ||
=== | === स्तरीय बनाम अशांत प्रवाह === | ||
[[File:Laminar-turbulent transition.jpg|thumb|लामिना से अशांत प्रवाह में संक्रमण ]] | [[File:Laminar-turbulent transition.jpg|thumb|लामिना से अशांत प्रवाह में संक्रमण ]] | ||
प्रक्षोभित प्रवाह, जो पुनःसंचरण, [[एडीज]] और स्पष्ट [[यादृच्छिकता]] द्वारा अभिलक्षित है। वह प्रवाह जिसमें प्रक्षोभ प्रदर्शित नहीं होती है, [[लामिना|स्तरीय प्रवाह]] कहलाते है। केवल एडीज़ या पुनःसंचरण की उपस्थिति प्रक्षोभित प्रवाह का संकेत नहीं देती है - ये घटनाएं स्तरीय प्रवाह में भी हो सकती हैं। गणितीय रूप से, प्रक्षोभित प्रवाह को प्रायः [[रेनॉल्ड्स अपघटन]] के माध्यम से दर्शाया जाता है, जिसमें प्रवाह को एक [[औसत]] घटक और एक क्षोभ घटक के योग में विभाजित किया जाता है। | |||
यह माना जाता है कि | यह माना जाता है कि प्रक्षोभित प्रवाह का वर्णन [[नेवियर-स्टोक्स समीकरणों]] के उपयोग से अच्छी तरह किया जा सकता है। मध्यम रेनॉल्ड्स संख्याओं पर प्रक्षोभित प्रवाह का अनुकरण, नेवियर-स्टोक्स समीकरणों के आधार पर [[प्रत्यक्ष संख्यात्मक सिमुलेशन|प्रत्यक्ष संख्यात्मक अनुकरण]] (डीएनएस) द्वारा संभव होता है। प्रतिबंध उपयोग किए गए संगणक (कंप्यूटर) की शक्ति और समाधान कलन विधि की दक्षता पर निर्भर करते हैं। डीएनएस के परिणाम कुछ प्रवाहों के प्रयोगात्मक आँकड़े से अच्छी तरह सहमत पाए गए हैं।<ref>See, for example, Schlatter et al, Phys. Fluids 21, 051702 (2009); {{doi|10.1063/1.3139294}}</ref> | ||
अगले कुछ दशकों के लिए संगणनात्मक शक्ति की स्थिति को देखते हुए, अधिकांश प्रवाहों में रेनॉल्ड्स की संख्या बहुत अधिक है, क्योंकि डीएनएस एक व्यावहारिक विकल्प है।<ref name="pope4">{{Cite book|last=Pope|first=Stephen B.|title=Turbulent Flows|publisher=Cambridge University Press|year=2000|isbn=0-521-59886-9}}</ref> कोई भी उड़ान वाहन जो मानव को ले जाने के लिए काफी बड़ा ( L > 3 मी) है, 20 मीटर प्रति सेकंड से अधिक तेज गति से चलने वाला, डीएनएस अनुकरण की सीमा से काफी आगे (Re = 4 मिलियन) है। परिवहन विमान पंखो (जैसे कि [[एयरबस A300]] या [[बोइंग 747]] पर) में रेनॉल्ड्स संख्या 40 मिलियन (पंख कॉर्ड आयाम के आधार पर) है। इन वास्तविक जीवन प्रवाह समस्याओं को हल करने के लिए निकट भविष्य के लिए प्रक्षोभित मॉडल की आवश्यकता होती है। [[रेनॉल्ड्स-औसत नेवियर-स्टोक्स समीकरण]] (आरएएनएस) [[अशांति मॉडलिंग|प्रक्षोभित मॉडलिंग]] के साथ संयुक्त रूप से प्रक्षोभित प्रवाह के प्रभावों का एक मॉडल प्रदान करता है। इस तरह की मॉडलिंग मुख्य रूप से [[रेनॉल्ड्स तनाव]] द्वारा अतिरिक्त संवेग परिवर्तन प्रदान करती है, हालांकि प्रक्षोभ [[गर्मी|ऊष्मा]] और [[द्रव्यमान हस्तांतरण|द्रव्यमान परिवर्तन]] को भी बढ़ाती है। एक और आशाजनक पद्धति [[बड़ी एड़ी सिमुलेशन|लार्ज एडी सिमुलेशन]] (एलईएस) है, विशेष रूप से [[अलग एड़ी सिमुलेशन|डीटैचड एडी सिमुलेशन]] (डीईएस) के रूप में - जो आरएएनएस प्रक्षोभ मॉडलिंग और लार्ज एडी सिमुलेशन का एक संयोजन है। | |||
=== अन्य सन्निकटन === | === अन्य सन्निकटन === | ||
द्रव गतिशील समस्याओं के लिए | द्रव गतिशील समस्याओं के लिए सामान्यतः उपयोग किए जाने वाले कुछ संभावित अनुमान नीचे सूचीबद्ध हैं। | ||
* ''[[Bussinesq सन्निकटन|बौसिनेक सन्निकटन]],'' प्रायः मुक्त [[संवहन]] समस्याओं (जहां घनत्व में परिवर्तन कम होता है) में उपयोग किया जाता है तथा [[उछाल|उत्प्लावन]] बलों की गणना के अलावा घनत्व में भिन्नता की उपेक्षा करता है। | |||
* ''[[स्नेहन सिद्धांत]]'' और ''[[हेले-शॉ प्रवाह]]'' यह दिखाने के लिए डोमेन के बड़े [[पहलू अनुपात|मुखानुपात]] का उपयोग करते हैं कि समीकरणों में कुछ पद छोटे हैं और इसलिए उन्हें उपेक्षित किया जा सकता है। | |||
* ''[[स्लेंडर-बॉडी थ्योरी|कृश पिंड सिद्धांत]]'' का उपयोग [[स्टोक्स प्रवाह]] समस्याओं में बल या श्यान द्रव में एक लंबी पतली वस्तु के चारों ओर प्रवाह क्षेत्र का अनुमान लगाने के लिए किया जाता है। | |||
* ''[[उथले-पानी के समीकरणों]]'' का उपयोग एक [[मुक्त सतह]] के साथ अपेक्षाकृत अश्यान तरल पदार्थ की एक परत का वर्णन करने के लिए किया जा सकता है, जिसमें सतह की [[ढाल]] कम होती हैं। | |||
* ''[[डार्सी के नियम]]'' का उपयोग [[झरझरा मीडिया|छिद्रित माध्यम]] में प्रवाह के लिए किया जाता है, और कई छिद्र-चौड़ाई पर औसत चर के साथ काम करता है। | |||
* घूर्णन प्रणालियों में, ''[[अर्ध-भू-भूगर्भीय समीकरण|भूविक्षेपी कल्प समीकरण]]'' [[दबाव प्रवणता]] और [[कोरिओलिस बल]] के बीच लगभग [[पूर्ण संतुलन]] मान लेते हैं। यह [[वायुमंडलीय गतिकी]] के अध्ययन में उपयोगी है। | |||
== | == बहुआयामी प्रकार == | ||
=== मच व्यवस्था के अनुसार प्रवाह === | |||
जबकि कई प्रवाह (जैसे कि एक पाइप के माध्यम से पानी का प्रवाह) कम [[मच संख्या]] ([[सबसोनिक|अवध्वानिक प्रवाह]]) पर होते है, वायुगतिकी या [[टर्बोमशीन]] में व्यावहारिक रुचि के कई प्रवाह {{Math|[[Mach number|''M'' {{=}} 1]]}} ([[ट्रांसोनिक प्रवाह|आध्वनिक प्रवाह]]) के उच्च अंशों पर या इससे अधिक ([[सुपरसोनिक|अतिध्वानिक]] या [[हाइपरसोनिक प्रवाह|अतिपराध्वनिक प्रवाह]]) होते हैं। इन व्यवस्थाओं में नई घटनाएं घटित होती हैं जैसे कि आध्वनिक प्रवाह में अस्थिरता, अतिध्वानिक प्रवाह के लिए आघात तरंग, या अतिपराध्वनिक प्रवाह में आयनीकरण के कारण रासायनिक आचरण असंतुलन। व्यवहारतः, उन प्रवाह व्यवस्थाओं में से प्रत्येक को अलग से व्यवहार किया जाता है। | |||
=== | === प्रतिक्रियाशील बनाम अनभिक्रियाशील प्रवाह === | ||
प्रतिक्रियाशील प्रवाह रासायनिक रूप से प्रतिक्रियाशील होते हैं, जिनके [[दहन]] ([[आईसी इंजन]]), [[नोदन]] युक्ति ([[रॉकेट]], [[जेट इंजन]], और इसी तरह), [[विस्फोट]], आग और सुरक्षा खतरों और खगोल भौतिकी सहित कई क्षेत्रों में कई अनुप्रयोग है। द्रव्यमान, संवेग और ऊर्जा के संरक्षण के अलावा, विशेष प्रजाति के संरक्षण (उदाहरण के लिए, मीथेन दहन में [[मीथेन]] का द्रव्यमान अंश) को प्राप्त करने की आवश्यकता होती है, जहां किसी भी प्रजाति के उत्पादन/कमी की दर एक साथ [[रासायनिक|रासायनिक बलगतिकी]] समीकरणों को हल करके प्राप्त की जाती है। | |||
=== | === चुंबक द्रव गतिकी (मैग्नेटोहाइड्रोडायनामिक्स) === | ||
चुंबक द्रव गतिकी ([[मैग्नेटोहाइड्रोडायनामिक्स]]) [[विद्युत चुम्बकीय]] क्षेत्रों में [[वैद्युत चालक]] तरल पदार्थों (उदाहरण, [[प्लाज़्मा]], तरल धातु और [[खारे पानी]]) के प्रवाह का बहु-विषयक अध्ययन है। द्रव प्रवाह समीकरणों को [[मैक्सवेल के विद्युत चुंबकत्व के समीकरणों]] के साथ-साथ हल किया जाता है। | |||
=== द्रव | ===सापेक्ष द्रव गतिकी === | ||
{{ | सापेक्षिक द्रव गतिकी [[प्रकाश के वेग की]] तुलना में अधिक वेगों पर असूक्ष्म और सूक्ष्म द्रव गति का अध्ययन करती है।<ref>{{Cite book|last=Landau|first=Lev Davidovich|author-link=Lev Landau|author-link2=Evgeny Lifshitz|first2=Evgenii Mikhailovich|last2=Lifshitz|title=Fluid Mechanics|location=London|publisher=Pergamon|year=1987|isbn=0-08-033933-6}}</ref> द्रव गतिकी की यह शाखा सापेक्षता के विशेष सिद्धांत और [[सापेक्षता के सामान्य सिद्धांत]] दोनों से सापेक्षतावादी प्रभावों के लिए जिम्मेदार है। नियंत्र समीकरण [[मिन्कोवस्की स्पेसटाइम|मिन्कोवस्की अवकाशकाल]] के लिए [[रिमेंनियन ज्यामिति]] में व्युत्पन्न हैं। | ||
== | == शब्दावली == | ||
दाब की अवधारणा द्रव स्थैतिक और द्रव गतिकी दोनों के अध्ययन के लिए केंद्रीय है। द्रव के मुख्य भाग में प्रत्येक बिंदु के लिए दाब अभिज्ञात किया जा सकता है, भले ही द्रव गति में हो या नहीं। दाब को निर्द्रव, बोरडॉन नलिका, मरकरी कॉलम या कई अन्य तरीकों का उपयोग करके [[मापा]] जा सकता है। | |||
द्रव गतिकी के अध्ययन में आवश्यक कुछ शब्दावली अध्ययन के अन्य समान क्षेत्रों में नहीं पाई जाती है। विशेष रूप से, द्रव गतिकी में उपयोग की जाने वाली कुछ शब्दावली का उपयोग [[द्रव स्टैटिक्स|द्रव स्थैतिकी]] में नहीं किया जाता है। | |||
=== | === असंपीड्य द्रव गतिकी में शब्दावली === | ||
द्रव प्रवाहों के अध्ययन में महत्वपूर्ण कुल दाब और [[गतिशील दबाव|गतिक दाब]] की अवधारणाएं [[बर्नौली के समीकरण]] से उत्पन्न होती हैं। (ये दो दाब सामान्य अर्थों में दाब नहीं हैं- इन्हें एरोइड, बौर्डन ट्यूब या पारा कॉलम का उपयोग करके मापा नहीं जा सकता है)। द्रव गतिकी में दाब की चर्चा करते समय संभावित अस्पष्टता से बचने के लिए, कई लेखक इसे कुल दाब और गतिकी दाब से अलग करने के लिए [[स्थिर दबाव|स्थैतिक दाब]] शब्द का उपयोग करते हैं। [[स्थैतिक दबाव दबाव|स्थैतिक दाब]] द्रव प्रवाह क्षेत्र में प्रत्येक बिंदु के लिए प्राप्त किया जा सकता है। | |||
द्रव प्रवाह में वह बिंदु जहाँ प्रवाह विराम अवस्था में हो (अर्थात् द्रव प्रवाह में अवगाहित किसी ठोस पिंड के समीप गति शून्य के बराबर हो), [[ठहराव बिंदु|प्रगतिरोध बिंदु]] कहलता है जिसका का विशेष महत्व है। प्रगतिरोध बिंदु पर स्थैतिक दाब [[ठहराव दबाव|प्रगतिरोध दाब]] कहलता है। असंपीड्य प्रवाह में, प्रगतिरोध बिंदु पर प्रगतिरोध दाब पूरे प्रवाह क्षेत्र में कुल दाब के बराबर होता है। | |||
=== संपीड़ित द्रव गतिकी में शब्दावली === | |||
एक संपीड़ित द्रव में, सभी ऊष्मागतिकी अवस्था गुणों (जैसे कुल तापमान, कुल एन्थैल्पी, ध्वनि की कुल गति) के लिए कुल स्थितियों (जिन्हें निष्क्रियता की स्थिति भी कहा जाता है) को परिभाषित करना आसन होता है। ये कुल प्रवाह की स्थितियाँ द्रव वेग का फलन है और अलग-अलग गति के निर्देश तंत्र में अलग-अलग मान हैं। | |||
स्थैतिक स्थितियां निर्देश तंत्र से स्वतंत्र हैं। "स्थैतिक" उपसर्ग का उपयोग साधारणतः द्रव की गति के बजाय द्रव की स्थिति से जुड़े द्रव के गुणों (जैसे स्थैतिक तापमान और स्थैतिक एन्थैल्पी) की चर्चा की जाने पर संभावित अस्पष्टता से बचने के लिए किया जाता है। कोई उपसर्ग ना होने पर द्रव गुण, स्थैतिक स्थिति होती है (इसलिए "घनत्व" और "स्थैतिक घनत्व" का अर्थ एक ही बात है)। | |||
कुल [[एन्ट्रॉपी]] और स्थिर एन्ट्रॉपी के बीच अंतर करने की कोई आवश्यकता नहीं है क्योंकि कुल प्रवाह की स्थिति, तरल पदार्थ को समस्थानिक रूप से विराम मे लाने के द्वारा परिभाषित किया जाता है। | |||
== | == संदर्भ निर्देश == | ||
{{Reflist}} | {{Reflist}} | ||
== | == अतिरिक्त पाठ्यसामग्री == | ||
* {{cite book|last=Acheson|first=D. J.|title=Elementary Fluid Dynamics|publisher=Clarendon Press|year=1990|isbn=0-19-859679-0}} | * {{cite book|last=Acheson|first=D. J.|title=Elementary Fluid Dynamics|publisher=Clarendon Press|year=1990|isbn=0-19-859679-0}} | ||
* {{cite book|last=Batchelor|first=G. K.|author-link=George Batchelor|title=An Introduction to Fluid Dynamics|publisher=Cambridge University Press|year=1967|isbn=0-521-66396-2}} | * {{cite book|last=Batchelor|first=G. K.|author-link=George Batchelor|title=An Introduction to Fluid Dynamics|publisher=Cambridge University Press|year=1967|isbn=0-521-66396-2}} | ||
| Line 327: | Line 168: | ||
* [http://www.scholarpedia.org/article/Encyclopedia:Fluid_dynamics Encyclopedia: Fluid dynamics] [[Scholarpedia]] | * [http://www.scholarpedia.org/article/Encyclopedia:Fluid_dynamics Encyclopedia: Fluid dynamics] [[Scholarpedia]] | ||
== | == बाहरी लिंक == | ||
{{Commons category|Fluid dynamics}} | {{Commons category|Fluid dynamics}} | ||
* [http://web.mit.edu/hml/ncfmf.html National Committee for Fluid Mechanics Films (NCFMF)], containing films on several subjects in fluid dynamics (in [[RealMedia]] format) | * [http://web.mit.edu/hml/ncfmf.html National Committee for Fluid Mechanics Films (NCFMF)], containing films on several subjects in fluid dynamics (in [[RealMedia]] format) | ||
| Line 337: | Line 178: | ||
{{Seamanship}} | {{Seamanship}} | ||
{{Authority control}} | {{Authority control}} | ||
[[Category:Machine Translated Page]] | |||
[[Category: | [[Category:AC with 0 elements]] | ||
[[Category: | [[Category:Articles with short description]] | ||
[[Category: | [[Category:CS1]] | ||
[[Category: | [[Category:CS1 maint]] | ||
[[Category: Machine Translated Page]] | [[Category:Commons category link is locally defined]] | ||
[[Category:Exclude in print]] | |||
[[Category:Interwiki category linking templates]] | |||
[[Category:Interwiki link templates]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with red-linked authority control categories]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Pages with template loops]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikimedia Commons templates]] | |||
Latest revision as of 09:54, 4 August 2022

द्रव गतिकी, भौतिकी तथा अभियान्त्रिकी में द्रव यांत्रिकी का उपविषय है, जिसके अंतर्गत तरल पदार्थों एवं गैसों के प्रवाह का अध्ययन किया जाता है। इसमें वायुगतिकी (गति में वायु तथा अन्य गैसों का अध्ययन) तथा हाइड्रोडायनामिक्स (गति में तरल पदार्थों का अध्ययन) सहित कई उप-विषय हैं। द्रव गतिकी में, विमान पर बल तथा आघुर्ण की गणना करना, पाइपलाइनों के माध्यम से पेट्रोलियम के द्रव्यमान प्रवाह दर का निर्धारण, मौसम का पूर्वानुमान लगाना, अंतर्तारकीय क्षेत्र में नेबुला को समझना एवं विखंडन हथियार विस्फोट का प्रतिरूपण जैसे अनुप्रयोगों कि एक विस्तृत श्रृंखला शामिल है।
द्रव गतिकी प्रयोगात्मक विषयों कि एक व्यवस्थित संरचना प्रदान करती है। जो प्रवाह माप से प्राप्त प्रयोगाश्रित एवं अर्ध-प्रयोगाश्रित नियमो का पालन करती है तथा प्रयोगात्मक समस्याओं को हल करने के लिए उपयोग की जाती है। द्रव गतिकी समस्या के हल के लिए प्राय: द्रव के विभिन्न गुणों जैसे कि स्थान तथा समय के फलन के रूप में, प्रवाह वेग, दाब, घनत्व तथा तापमान की गणना शामिल होती है।
बीसवीं शताब्दी से पहले, हाइड्रोडायनामिक्स द्रव गतिकी का पर्याय था। यह अभी भी कुछ द्रव गतिकी विषयों जैसे मैग्नेटोहाइड्रोडायनामिक्स तथा हाइड्रोडायनामिक स्थिरता के नामों मे परिलक्षित होता है, जो दोनों को गैसों पर भी लागू किया जा सकता है।[1]
समीकरण
द्रव गतिकी मे चिरसम्मत यांत्रिकी पर आधारित, द्रव्यमान का संरक्षण, रेखीये संवेग का संरक्षण, तथा ऊर्जा का संरक्षण (जिसे उष्मागतिकी का पहला नियम भी कहा जाता है) जैसे मूलभूत स्वयंसिद्ध संरक्षण नियम हैं। जिन्हे क्वांटम यांत्रिकी तथा सामान्य सापेक्षता में संशोधित किया गया हैं। वे रेनॉल्ड्स आवेग प्रमेय का उपयोग करके व्यक्त किए जाते हैं।
उपरोक्त के अलावा, तरल पदार्थ अणुओं से बने होते हैं जो एक दूसरे से तथा ठोस वस्तुओं से टकराते हैं तथा सातत्य धारणा का पालन करते हैं। हालांकि, सातत्य धारणा के अनुसार तरल पदार्थ असतत के बजाय सतत होते हैं, जिसके परिणामस्वरूप, अंतरिक्ष में असीम रूप से छोटे बिंदुओं पर घनत्व, दाब, तापमान तथा प्रवाह वेग जैसे गुण अच्छी तरह से परिभाषित होते हैं तथा एक बिंदु से दूसरे बिंदु पर लगातार भिन्न होते हैं।
तरल पदार्थ जो सातत्य होने के लिए पर्याप्त रूप से सघन होते हैं, जिनमें आयनिक प्रजातियां नहीं होती हैं तथा प्रकाश की गति के संबंध में प्रवाह वेग छोटा होता है, नेवियर-स्टोक्स समीकरण अवकल समीकरणों का अरैखिक समुच्चय है, जो न्यूटोनियन तरल पदार्थों के लिए गति समीकरण होता है तथा तरल पदार्थ के प्रवाह का वर्णन करता है, जिसका तनाव प्रवाह वेग ढाल तथा दाब पर रैखिक रूप से निर्भर करता है। सरलीकृत समीकरणों में एक सामान्य संवृत रूप हल नहीं होता है, इसलिए वे मुख्य रूप से संगणनात्मक तरल गतिकी में उपयोग किए जाते हैं। समीकरणों को कई तरीकों से हल किया जा सकता है। कुछ सरलीकरण कुछ सरल द्रव गतिकी समस्याओं को संवृत रूप में हल करने की अनुमति देते हैं।
द्रव्यमान, संवेग तथा ऊर्जा संरक्षण समीकरणों के अलावा, समस्या के पूर्ण वर्णन के लिए, ऊष्मागतिकी अवस्था समीकरण जिसमे दाब अन्य ऊष्मागतिकी चर का फलन होता है, की आवश्यकता होती है। इसका एक उदाहरण आदर्श गैस का अवस्था समीकरण है।
जहां p दाब, ρ घनत्व, T पूर्ण तापमान, Ru गैस स्थिरांक तथा M एक विशेष गैस के लिए मोलर द्रव्यमान है।
संरक्षण नियम
द्रव गतिकी समस्याओं को हल करने के लिए तीन संरक्षण नियमो का उपयोग किया जाता है, जिन्हे समाकल या अवकल रूप में लिखा जाता है। संरक्षण नियम प्रवाह के क्षेत्र पर लागू किया जा सकता है जिसे नियंत्रण खंड कहा जाता है। नियंत्रित आयतन अंतरिक्ष में असतत आयतन है जिसके माध्यम से द्रव प्रवाहित होता है। नियंत्रित आयतन मे द्रव्यमान, गति या ऊर्जा के परिवर्तन का वर्णन संरक्षण नियमो के समाकल सूत्रीकरण के द्वार किया जाता है। संरक्षण नियमो के अवकल सूत्रीकरण एक समतुल्य संबंध उत्पन्न करने के लिए स्टोक्स के प्रमेय को लागू किया जाता है, जिसे प्रवाह में एक असीम रूप से छोटी मात्रा (एक बिंदु पर) पर लागू नियम के समाकल रूप के रूप में व्यखित किया जा सकता है।
द्रव्यमान सातत्य (द्रव्यमान का संरक्षण)
नियंत्रित आयतन मे द्रव द्रव्यमान के परिवर्तन की दर आयतन में द्रव प्रवाह की नेट दर के बराबर होनी चाहिए। भौतिक रूप से, नियंत्रित आयतन में द्रव्यमान न तो उत्पन्न किया जा सकता है और न ही नष्ट किया जा सकता है, और इसका सांतत्य समीकरण का समाकल रूप प्रदर्शित किया गया है।
उपरोक्त समीकरण मे द्रव घनत्व ह, u प्रवाह वेग सदिश तथा t समय है। उपरोक्त समीकरण के बाएं हाथ की मात्रा मे द्रव्यमान की वृद्धि की दर तथा नियंत्रित आयतन पर एक त्रि-समकालन है, जबकि दायीं ओर निकाय मे संवहित द्रव्यमान के नियंत्रित आयतन की सम्पूर्ण सतह के लिए समकालन है। निकाय मे द्रव्यमान प्रवाह को सकारात्मक माना जाता है, अपसरण प्रमेय द्वारा सातत्य समीकरण का अवकल रूप नीचे दिए गए समीकरण द्वारा प्रदर्शित किया जा सकता है।
गति का संरक्षण
न्यूटन के गति का दूसरा नियम नियंत्रित आयतन पर लागू होता है, यह एक कथन है कि नियंत्रित आयतन मे द्रव के संवेग में कोई भी परिवर्तन आयतन में संवेग के शुद्ध प्रवाह तथा आयतन मे द्रव पर कार्य करने वाले बाहरी बलों की क्रिया के कारण होता है।
इस समीकरण के उपरोक्त समाकल सूत्रीकरण में, बाईं ओर का पद मात्रा में संवेग का नेट परिवर्तन है। दायीं ओर का पहला पद नेट दर है जिस पर संवेग आयतन में संवहित होता है और दूसरा पद आयतन की सतहों पर दाब के कारण लगने वाला बल है। निकाय में प्रवेश करने वाले संवेग के धनात्मक होने के कारण दायीं ओर के पहले दो पदों को अस्वीकार कर दिया जाता है, और सामान्य वेग u और दाब बलों की दिशा के विपरीत होता है। दायीं ओर का तीसरा पद किसी भी पिंड बल (यहाँ fbody द्वारा दर्शाया गया है) के कारण आयतन मे द्रव्यमान का नेट त्वरण है। सतही बल, जैसे श्यान बल, Fsurf द्वारा दर्शाए जाते हैं, जो आयतन सतह पर कार्य करने वाले अपरूपण बलों के कारण नेट बल होता है। संवेग संतुलन को गतिमान नियंत्रित आयतन के लिए भी लिखा जा सकता है। संवेग संरक्षण समीकरण का अवकल रूप निम्नलिखित है। यहां आयतन को एक छोटे से छोटे बिंदु तक कम कर दिया जाता है, और सतह और पिंड की शक्ति दोनों को कुल बल F के लिए जिम्मेदार बताया जाता है। उदाहरण के लिए, प्रवाह में F को एक बिंदु पर अभिनय करने वाले घर्षण और गुरुत्वाकर्षण बलों के लिए एक अभिव्यक्ति में विस्तारित किया जा सकता है।
वायुगतिकी में, हवा को न्यूटोनियन द्रव माना जाता है, जो अपरूपण तनाव (आंतरिक घर्षण बलों के कारण) तथा द्रव के तनाव की दर के बीच एक रैखिक संबंध रखता है। उपरोक्त समीकरण त्रि-विमीय प्रवाह में एक सदिश समीकरण है, लेकिन इसे तीन समन्वित दिशाओं में तीन अदिश समीकरणों के रूप में व्यक्त किया जा सकता है। संपीड़ित, श्यान प्रवाह के लिए संवेग संरक्षण के समीकरणों को नेवियर-स्टोक्स समीकरण कहा जाता है।
ऊर्जा का संरक्षण
यद्यपि ऊर्जा को एक रूप से दूसरे रूप में परिवर्तित किया जा सकता है, एक संवृत (बंद) निकाय में कुल ऊर्जा स्थिर रहती है।
उपरोक्त समीकरण मे h विशिष्ट एन्थैल्पी है, k द्रव की तापीय चालकता है, T तापमान और Φ श्यान अपव्यय फलन है, बाईं ओर का व्यंजक भौतिक व्युत्पन्न है। श्यान अपव्यय फलन उस दर को नियंत्रित करता है, जिस पर प्रवाह की यांत्रिक ऊर्जा उष्मा में परिवर्तित हो जाती है। ऊष्मागतिकी के दूसरे नियम के लिए अपव्यय पद हमेशा सकारात्मक होना आवश्यक है। श्यान्ता नियंत्रित आयतन मे ऊर्जा नहीं बना सकता है।[2]
वर्गीकरण
संपीड़ित की तुलना में असंपीड़ित प्रवाह
सभी तरल पदार्थ एक सीमा तक संकुचित होते हैं, अर्थात् दाब या तापमान में परिवर्तन से घनत्व में परिवर्तन होता है। हालांकि, कई स्थितियों में दाब और तापमान में परिवर्तन इतना कम होता है कि घनत्व में बदलाव नगण्य होता है। इस स्थिति में प्रवाह को एक असम्पीडित प्रवाह के रूप में प्रतिदर्श किया जा सकता है। अन्यथा अधिक सामान्य संपीड़ित प्रवाह समीकरणों का उपयोग किया जा सकता है।
गणितीय रूप से, ρ को यह कहकर व्यक्त किया जाता है कि द्रव पार्सल का घनत्व प्रवाह क्षेत्र में गति करने पर नहीं बदलता है, अर्थात,
जहां पर D/Dt द्रव्यात्मक अवकलज है, जो क्षेत्रीय और संवहनी अवकलज का योग है। एक समान घनत्व के द्रव कि स्थिति में यह अतिरिक्त अवरोध नियंत्र समीकरणों को सरल बनाते है।
प्रवाह की मच संख्या के मूल्यांकन द्वार गैसों के प्रवाह के लिए, संपीड़ित या असंपीड़ित द्रव गतिकी में उपयोगी को निर्धारित करते है। एक मोटे मार्गदर्शक के रूप में, लगभग 0.3 से नीचे मच संख्या पर संपीड़ित प्रभावों को अनदेखा किया जा सकता है। तरल पदार्थों के लिए, क्या असंपीड़ित धारणा वैध है, द्रव गुणों (विशेष रूप से महत्वपूर्ण दाब और तरल पदार्थ का तापमान) और प्रवाह की स्थिति (वास्तविक प्रवाह दाब कितना महत्वपूर्ण दाब बन जाता है) पर निर्भर करता है। ध्वनि तरंगें संपीड़न तरंगें होती हैं, अत: ध्वनिक समस्याओं के लिए हमेशा संपीड्यता की अनुमति की आवश्यकता होती है, क्योंकि जिनमें दाब में परिवर्तन और माध्यम के घनत्व में परिवर्तन के माध्यम से तरल पदार्थ फैलते हैं।
न्यूटोनियन बनाम अ-न्यूटोनियन तरल पदार्थ
अति तरल को छोड़कर सभी तरल पदार्थ विरूपण के लिए कुछ प्रतिरोध रखते है अर्थात श्यान होते हैं। विभिन्न वेगों पर चलने वाले तरल पदार्थ के निकटवर्ती पार्सल एक दूसरे पर श्यान बल लगाते हैं। वेग प्रवणता को तनाव दर के रूप में संदर्भित किया जाता है, इसका विमा T −1 है। आइजैक न्यूटन ने बताया कि पानी और हवा जैसे कई परिचित तरल पदार्थों के लिए, इन श्यान बलों के कारण तनाव रैखिक रूप से तनाव दर से संबंधित होता है। ऐसे द्रवों को न्यूटोनियन द्रव कहते हैं। न्यूटोनियन तरल पदार्थों के लिए तनाव दर से स्वतंत्र आनुपातिकता के गुणांक को द्रव की श्यानता (यह एक द्रव गुण है) कहा जाता है।
अ-न्यूटोनियन तरल पदार्थों में अधिक जटिल, अरेखीय तनाव - खिंचाव व्यवहार होता है। प्रवाहिकी का उप संकाय ऐसे तरल पदार्थों के तनाव - खिंचाव व्यवहार का वर्णन करता है, जिसमें पायस और घोल, कुछ श्यानप्रत्यास्थ सामग्री जैसे रक्त और कुछ बहुलक, और श्यान तरल पदार्थ जैसे लेटेक्स, शहद और स्नेहक शामिल हैं। [3]
अश्यान बनाम श्यान बनाम स्टोक्स प्रवाह
द्रव पार्सल की गतिशीलता का वर्णन न्यूटन के दूसरे नियम के द्वरा किया गया है। द्रव का त्वरित पार्सल जड़त्वीय प्रभावों के अधीन है।
रेनॉल्ड्स संख्या एक विमाहीन मात्रा है जो श्यान प्रभावों के परिमाण की तुलना में जड़त्वीय प्रभावों के परिमाण की विशेषता है। छोटी रेनॉल्ड्स संख्या (Re ≪ 1) इंगित करती है कि श्यान बल जड़त्वीय बलों की तुलना में बहुत शक्तिशालि हैं। ऐसी स्थिति में, जड़त्वीय बलों की कभी-कभी उपेक्षा की जाती है, इस प्रवाह व्यवस्था को स्टोक्स या रेंगने वाला प्रवाह कहा जाता है।
इसके विपरीत, उच्च रेनॉल्ड्स संख्या (Re ≫ 1) इंगित करती है कि श्यान (घर्षण) प्रभावों की तुलना में जड़त्वीय प्रभाव वेग क्षेत्र पर अधिक प्रभाव डालते हैं। उच्च रेनॉल्ड्स संख्या प्रवाह में, प्रवाह को प्रायः अश्यान प्रवाह (अनुमान जिसमें श्यानता पूरी तरह से उपेक्षित होता है) के रूप में तैयार किया जाता है। श्यानता को खत्म करने से नेवियर-स्टोक्स समीकरणों को यूलर समीकरणों में सरल किया जा सकता है। यूलर समीकरणों का समाकलन अप्रत्यक्ष प्रवाह में एक धारा के साथ बर्नौली के समीकरण को उत्पन्न करता है। जब, अश्यान होने के अलावा, प्रवाह हर जगह अघूर्णी होता है, अतः बर्नौली का समीकरण हर जगह प्रवाह का पूरी तरह से वर्णन कर सकता है। इस तरह के प्रवाह को संभावित प्रवाह कहा जाता है, क्योंकि वेग क्षेत्र को स्थितिज ऊर्जा व्यंजक की प्रवणता के रूप में व्यक्त किया जा सकता है।
हालांकि, ठोस सीमाओं को शामिल करने वाली समस्याओं के लिए श्यानता को शामिल करने की आवश्यकता हो सकती है। ठोस सीमाओं के पास श्यानता की उपेक्षा नहीं की जा सकती है, क्योंकि नो-स्लिप स्थिति बड़े तनाव दर, सीमा परत का एक पतला क्षेत्र उत्पन्न करती है, जिसमें श्यानता प्रभावी होता है और इस प्रकार भंवर उत्पन्न करता है। इसलिए, निकायों (जैसे पंख) पर नेट बलों की गणना करने के लिए, श्यान प्रवाह समीकरणों का उपयोग किया जाना चाहिए। अश्यान प्रवाह सिद्धांत संकर्ष बल की भविष्यवाणी करने में विफल रहता है, एक सीमा जिसे डी'एलेम्बर्ट के विरोधाभास के रूप में जाना जाता है।
प्रायः इस्तेमाल किया जाने वाला मॉडल[4], विशेष रूप से संगणनात्मक तरल गतिकी में, दो प्रवाह मॉडल (पिंड से दूर यूलर समीकरण, और पिंड के करीब एक क्षेत्र में सीमा परत समीकरण) का उपयोग किया जाता है। मिलान किए गए स्पर्शोन्मुख विस्तार की विधि का उपयोग करके दो समाधानों का एक दूसरे के साथ मिलान किया जा सकता है।
स्थिर बनाम अस्थिर प्रवाह
प्रवाह जो समय का फलन नहीं होता, स्थिर प्रवाह कहलाता है। स्थिर-अवस्था प्रवाह उस स्थिति को संदर्भित करता है जहां निकाय में एक बिंदु पर द्रव गुण समय के साथ नहीं बदलते हैं। समय पर निर्भर प्रवाह को अस्थिर (क्षणिक [5]) के रूप में जाना जाता है। चाहे कोई विशेष प्रवाह स्थिर हो या अस्थिर, निर्देश आधार पर निर्भर हो सकता है। उदाहरण के लिए, एक गोले के संबंध में स्थिर निर्देश आधार में गोले पर स्तरीय प्रवाह स्थिर होता है। निर्देश आधार में जो पृष्ठभूमि प्रवाह के संबंध में स्थिर है, प्रवाह अस्थिर है।
अशांत प्रवाह परिभाषा के अनुसार अस्थिर हैं। हालांकि, अशांत प्रवाह सांख्यिकीय रूप से स्थिर हो सकता है। यादृच्छिक वेग क्षेत्र U(x, t), यदि सभी आँकड़े समय में बदलाव के तहत अपरिवर्तनीय हो[6], सांख्यिकीय रूप से स्थिर होता हैं।[7] इसका मोटे तौर पर मतलब है कि सभी सांख्यिकीय गुण समय में स्थिर हैं। प्रायः माध्य क्षेत्र रुचि का विषय होता है, और यह सांख्यिकीय रूप से स्थिर प्रवाह में भी स्थायी होता है।
स्थिर प्रवाह प्रायः समान अस्थिर प्रवाह की तुलना में अधिक सुविधाजनक होते हैं। एक स्थिर समस्या के नियंत्र समीकरणों में प्रवाह क्षेत्र की स्थिरता का लाभ उठाए बिना एक ही समस्या के शासी समीकरणों की तुलना में कम आयाम (समय) होता है।
स्तरीय बनाम अशांत प्रवाह
प्रक्षोभित प्रवाह, जो पुनःसंचरण, एडीज और स्पष्ट यादृच्छिकता द्वारा अभिलक्षित है। वह प्रवाह जिसमें प्रक्षोभ प्रदर्शित नहीं होती है, स्तरीय प्रवाह कहलाते है। केवल एडीज़ या पुनःसंचरण की उपस्थिति प्रक्षोभित प्रवाह का संकेत नहीं देती है - ये घटनाएं स्तरीय प्रवाह में भी हो सकती हैं। गणितीय रूप से, प्रक्षोभित प्रवाह को प्रायः रेनॉल्ड्स अपघटन के माध्यम से दर्शाया जाता है, जिसमें प्रवाह को एक औसत घटक और एक क्षोभ घटक के योग में विभाजित किया जाता है।
यह माना जाता है कि प्रक्षोभित प्रवाह का वर्णन नेवियर-स्टोक्स समीकरणों के उपयोग से अच्छी तरह किया जा सकता है। मध्यम रेनॉल्ड्स संख्याओं पर प्रक्षोभित प्रवाह का अनुकरण, नेवियर-स्टोक्स समीकरणों के आधार पर प्रत्यक्ष संख्यात्मक अनुकरण (डीएनएस) द्वारा संभव होता है। प्रतिबंध उपयोग किए गए संगणक (कंप्यूटर) की शक्ति और समाधान कलन विधि की दक्षता पर निर्भर करते हैं। डीएनएस के परिणाम कुछ प्रवाहों के प्रयोगात्मक आँकड़े से अच्छी तरह सहमत पाए गए हैं।[8]
अगले कुछ दशकों के लिए संगणनात्मक शक्ति की स्थिति को देखते हुए, अधिकांश प्रवाहों में रेनॉल्ड्स की संख्या बहुत अधिक है, क्योंकि डीएनएस एक व्यावहारिक विकल्प है।[9] कोई भी उड़ान वाहन जो मानव को ले जाने के लिए काफी बड़ा ( L > 3 मी) है, 20 मीटर प्रति सेकंड से अधिक तेज गति से चलने वाला, डीएनएस अनुकरण की सीमा से काफी आगे (Re = 4 मिलियन) है। परिवहन विमान पंखो (जैसे कि एयरबस A300 या बोइंग 747 पर) में रेनॉल्ड्स संख्या 40 मिलियन (पंख कॉर्ड आयाम के आधार पर) है। इन वास्तविक जीवन प्रवाह समस्याओं को हल करने के लिए निकट भविष्य के लिए प्रक्षोभित मॉडल की आवश्यकता होती है। रेनॉल्ड्स-औसत नेवियर-स्टोक्स समीकरण (आरएएनएस) प्रक्षोभित मॉडलिंग के साथ संयुक्त रूप से प्रक्षोभित प्रवाह के प्रभावों का एक मॉडल प्रदान करता है। इस तरह की मॉडलिंग मुख्य रूप से रेनॉल्ड्स तनाव द्वारा अतिरिक्त संवेग परिवर्तन प्रदान करती है, हालांकि प्रक्षोभ ऊष्मा और द्रव्यमान परिवर्तन को भी बढ़ाती है। एक और आशाजनक पद्धति लार्ज एडी सिमुलेशन (एलईएस) है, विशेष रूप से डीटैचड एडी सिमुलेशन (डीईएस) के रूप में - जो आरएएनएस प्रक्षोभ मॉडलिंग और लार्ज एडी सिमुलेशन का एक संयोजन है।
अन्य सन्निकटन
द्रव गतिशील समस्याओं के लिए सामान्यतः उपयोग किए जाने वाले कुछ संभावित अनुमान नीचे सूचीबद्ध हैं।
- बौसिनेक सन्निकटन, प्रायः मुक्त संवहन समस्याओं (जहां घनत्व में परिवर्तन कम होता है) में उपयोग किया जाता है तथा उत्प्लावन बलों की गणना के अलावा घनत्व में भिन्नता की उपेक्षा करता है।
- स्नेहन सिद्धांत और हेले-शॉ प्रवाह यह दिखाने के लिए डोमेन के बड़े मुखानुपात का उपयोग करते हैं कि समीकरणों में कुछ पद छोटे हैं और इसलिए उन्हें उपेक्षित किया जा सकता है।
- कृश पिंड सिद्धांत का उपयोग स्टोक्स प्रवाह समस्याओं में बल या श्यान द्रव में एक लंबी पतली वस्तु के चारों ओर प्रवाह क्षेत्र का अनुमान लगाने के लिए किया जाता है।
- उथले-पानी के समीकरणों का उपयोग एक मुक्त सतह के साथ अपेक्षाकृत अश्यान तरल पदार्थ की एक परत का वर्णन करने के लिए किया जा सकता है, जिसमें सतह की ढाल कम होती हैं।
- डार्सी के नियम का उपयोग छिद्रित माध्यम में प्रवाह के लिए किया जाता है, और कई छिद्र-चौड़ाई पर औसत चर के साथ काम करता है।
- घूर्णन प्रणालियों में, भूविक्षेपी कल्प समीकरण दबाव प्रवणता और कोरिओलिस बल के बीच लगभग पूर्ण संतुलन मान लेते हैं। यह वायुमंडलीय गतिकी के अध्ययन में उपयोगी है।
बहुआयामी प्रकार
मच व्यवस्था के अनुसार प्रवाह
जबकि कई प्रवाह (जैसे कि एक पाइप के माध्यम से पानी का प्रवाह) कम मच संख्या (अवध्वानिक प्रवाह) पर होते है, वायुगतिकी या टर्बोमशीन में व्यावहारिक रुचि के कई प्रवाह M = 1 (आध्वनिक प्रवाह) के उच्च अंशों पर या इससे अधिक (अतिध्वानिक या अतिपराध्वनिक प्रवाह) होते हैं। इन व्यवस्थाओं में नई घटनाएं घटित होती हैं जैसे कि आध्वनिक प्रवाह में अस्थिरता, अतिध्वानिक प्रवाह के लिए आघात तरंग, या अतिपराध्वनिक प्रवाह में आयनीकरण के कारण रासायनिक आचरण असंतुलन। व्यवहारतः, उन प्रवाह व्यवस्थाओं में से प्रत्येक को अलग से व्यवहार किया जाता है।
प्रतिक्रियाशील बनाम अनभिक्रियाशील प्रवाह
प्रतिक्रियाशील प्रवाह रासायनिक रूप से प्रतिक्रियाशील होते हैं, जिनके दहन (आईसी इंजन), नोदन युक्ति (रॉकेट, जेट इंजन, और इसी तरह), विस्फोट, आग और सुरक्षा खतरों और खगोल भौतिकी सहित कई क्षेत्रों में कई अनुप्रयोग है। द्रव्यमान, संवेग और ऊर्जा के संरक्षण के अलावा, विशेष प्रजाति के संरक्षण (उदाहरण के लिए, मीथेन दहन में मीथेन का द्रव्यमान अंश) को प्राप्त करने की आवश्यकता होती है, जहां किसी भी प्रजाति के उत्पादन/कमी की दर एक साथ रासायनिक बलगतिकी समीकरणों को हल करके प्राप्त की जाती है।
चुंबक द्रव गतिकी (मैग्नेटोहाइड्रोडायनामिक्स)
चुंबक द्रव गतिकी (मैग्नेटोहाइड्रोडायनामिक्स) विद्युत चुम्बकीय क्षेत्रों में वैद्युत चालक तरल पदार्थों (उदाहरण, प्लाज़्मा, तरल धातु और खारे पानी) के प्रवाह का बहु-विषयक अध्ययन है। द्रव प्रवाह समीकरणों को मैक्सवेल के विद्युत चुंबकत्व के समीकरणों के साथ-साथ हल किया जाता है।
सापेक्ष द्रव गतिकी
सापेक्षिक द्रव गतिकी प्रकाश के वेग की तुलना में अधिक वेगों पर असूक्ष्म और सूक्ष्म द्रव गति का अध्ययन करती है।[10] द्रव गतिकी की यह शाखा सापेक्षता के विशेष सिद्धांत और सापेक्षता के सामान्य सिद्धांत दोनों से सापेक्षतावादी प्रभावों के लिए जिम्मेदार है। नियंत्र समीकरण मिन्कोवस्की अवकाशकाल के लिए रिमेंनियन ज्यामिति में व्युत्पन्न हैं।
शब्दावली
दाब की अवधारणा द्रव स्थैतिक और द्रव गतिकी दोनों के अध्ययन के लिए केंद्रीय है। द्रव के मुख्य भाग में प्रत्येक बिंदु के लिए दाब अभिज्ञात किया जा सकता है, भले ही द्रव गति में हो या नहीं। दाब को निर्द्रव, बोरडॉन नलिका, मरकरी कॉलम या कई अन्य तरीकों का उपयोग करके मापा जा सकता है।
द्रव गतिकी के अध्ययन में आवश्यक कुछ शब्दावली अध्ययन के अन्य समान क्षेत्रों में नहीं पाई जाती है। विशेष रूप से, द्रव गतिकी में उपयोग की जाने वाली कुछ शब्दावली का उपयोग द्रव स्थैतिकी में नहीं किया जाता है।
असंपीड्य द्रव गतिकी में शब्दावली
द्रव प्रवाहों के अध्ययन में महत्वपूर्ण कुल दाब और गतिक दाब की अवधारणाएं बर्नौली के समीकरण से उत्पन्न होती हैं। (ये दो दाब सामान्य अर्थों में दाब नहीं हैं- इन्हें एरोइड, बौर्डन ट्यूब या पारा कॉलम का उपयोग करके मापा नहीं जा सकता है)। द्रव गतिकी में दाब की चर्चा करते समय संभावित अस्पष्टता से बचने के लिए, कई लेखक इसे कुल दाब और गतिकी दाब से अलग करने के लिए स्थैतिक दाब शब्द का उपयोग करते हैं। स्थैतिक दाब द्रव प्रवाह क्षेत्र में प्रत्येक बिंदु के लिए प्राप्त किया जा सकता है।
द्रव प्रवाह में वह बिंदु जहाँ प्रवाह विराम अवस्था में हो (अर्थात् द्रव प्रवाह में अवगाहित किसी ठोस पिंड के समीप गति शून्य के बराबर हो), प्रगतिरोध बिंदु कहलता है जिसका का विशेष महत्व है। प्रगतिरोध बिंदु पर स्थैतिक दाब प्रगतिरोध दाब कहलता है। असंपीड्य प्रवाह में, प्रगतिरोध बिंदु पर प्रगतिरोध दाब पूरे प्रवाह क्षेत्र में कुल दाब के बराबर होता है।
संपीड़ित द्रव गतिकी में शब्दावली
एक संपीड़ित द्रव में, सभी ऊष्मागतिकी अवस्था गुणों (जैसे कुल तापमान, कुल एन्थैल्पी, ध्वनि की कुल गति) के लिए कुल स्थितियों (जिन्हें निष्क्रियता की स्थिति भी कहा जाता है) को परिभाषित करना आसन होता है। ये कुल प्रवाह की स्थितियाँ द्रव वेग का फलन है और अलग-अलग गति के निर्देश तंत्र में अलग-अलग मान हैं।
स्थैतिक स्थितियां निर्देश तंत्र से स्वतंत्र हैं। "स्थैतिक" उपसर्ग का उपयोग साधारणतः द्रव की गति के बजाय द्रव की स्थिति से जुड़े द्रव के गुणों (जैसे स्थैतिक तापमान और स्थैतिक एन्थैल्पी) की चर्चा की जाने पर संभावित अस्पष्टता से बचने के लिए किया जाता है। कोई उपसर्ग ना होने पर द्रव गुण, स्थैतिक स्थिति होती है (इसलिए "घनत्व" और "स्थैतिक घनत्व" का अर्थ एक ही बात है)।
कुल एन्ट्रॉपी और स्थिर एन्ट्रॉपी के बीच अंतर करने की कोई आवश्यकता नहीं है क्योंकि कुल प्रवाह की स्थिति, तरल पदार्थ को समस्थानिक रूप से विराम मे लाने के द्वारा परिभाषित किया जाता है।
संदर्भ निर्देश
- ↑ Eckert, Michael (2006). The Dawn of Fluid Dynamics: A Discipline Between Science and Technology. Wiley. p. ix. ISBN 3-527-40513-5.
- ↑ White, F. M. (1974). Viscous Fluid Flow. New York: McGraw–Hill. ISBN 0-07-069710-8.
- ↑ Wilson, DI (February 2018). "What is Rheology?". Eye. 32 (2): 179–183. doi:10.1038/eye.2017.267. PMC 5811736. PMID 29271417.
- ↑ Platzer, B. (2006-12-01). "Book Review: Cebeci, T. and Cousteix, J., Modeling and Computation of Boundary-Layer Flows". ZAMM. 86 (12): 981–982. doi:10.1002/zamm.200690053. ISSN 0044-2267.
- ↑ "Transient state or unsteady state? -- CFD Online Discussion Forums". www.cfd-online.com.
- ↑ Pope, Stephen B. (2000). Turbulent Flows. Cambridge University Press. ISBN 0-521-59886-9.
- ↑ Pope, Stephen B. (2000). Turbulent Flows. Cambridge University Press. ISBN 0-521-59886-9.
- ↑ See, for example, Schlatter et al, Phys. Fluids 21, 051702 (2009); doi:10.1063/1.3139294
- ↑ Pope, Stephen B. (2000). Turbulent Flows. Cambridge University Press. ISBN 0-521-59886-9.
- ↑ Landau, Lev Davidovich; Lifshitz, Evgenii Mikhailovich (1987). Fluid Mechanics. London: Pergamon. ISBN 0-08-033933-6.
अतिरिक्त पाठ्यसामग्री
- Acheson, D. J. (1990). Elementary Fluid Dynamics. Clarendon Press. ISBN 0-19-859679-0.
- Batchelor, G. K. (1967). An Introduction to Fluid Dynamics. Cambridge University Press. ISBN 0-521-66396-2.
- Chanson, H. (2009). Applied Hydrodynamics: An Introduction to Ideal and Real Fluid Flows. CRC Press, Taylor & Francis Group, Leiden, The Netherlands, 478 pages. ISBN 978-0-415-49271-3.
- Clancy, L. J. (1975). Aerodynamics. London: Pitman Publishing Limited. ISBN 0-273-01120-0.
- Lamb, Horace (1994). Hydrodynamics (6th ed.). Cambridge University Press. ISBN 0-521-45868-4. Originally published in 1879, the 6th extended edition appeared first in 1932.
- Milne-Thompson, L. M. (1968). Theoretical Hydrodynamics (5th ed.). Macmillan. Originally published in 1938.
- Shinbrot, M. (1973). Lectures on Fluid Mechanics. Gordon and Breach. ISBN 0-677-01710-3.
- Nazarenko, Sergey (2014), Fluid Dynamics via Examples and Solutions, CRC Press (Taylor & Francis group), ISBN 978-1-43-988882-7
- Encyclopedia: Fluid dynamics Scholarpedia
बाहरी लिंक
- National Committee for Fluid Mechanics Films (NCFMF), containing films on several subjects in fluid dynamics (in RealMedia format)
- List of Fluid Dynamics books