गैर-समान तर्कसंगत बी-स्पलाइन: Difference between revisions
No edit summary |
No edit summary |
||
| (33 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Method of representing curves and surfaces in computer graphics}} | {{Short description|Method of representing curves and surfaces in computer graphics}} | ||
[[File:NURBstatic.svg|thumb|250px|एक | [[File:NURBstatic.svg|thumb|250px|एक एनयूआरबीएस वक्र।(यह भी देखें: एनयूआरबीएस स्पलाइन की एनिमेटेड रचना।)]] | ||
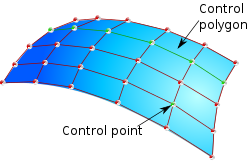
[[File:NURBS surface.png|alt=Green-shaded NURBS surface|thumb|250px|एक | [[File:NURBS surface.png|alt=Green-shaded NURBS surface|thumb|250px|एक एनयूआरबीएस सतह]] | ||
एनयूआरबीएस(नॉन-यूनिफार्म रैशनल बेसिस स्पलाइन) एक गणितीय मॉडल है। जो आधार विभाजन(बेसिस स्पलाइन) का उपयोग करता है। जो कंप्यूटर ग्राफिक्स वक्र में और इसके सतहों के प्रतिनिधित्व के लिए उपयोग किया जाता है। यह विश्लेषणात्मक(गणितीय सूत्रों द्वारा परिभाषित) और प्रतिरूपित आकृतियों को संभालने के लिए बहुत लचीलापन और सटीकता प्रदान करता है। यह एक प्रकार का वक्र प्रतिरूपण है, जो बहुभुज प्रतिरूपण या डिजिटल वास्तुशिल्प के विपरीत है। एनयूआरबीएस वक्र सामान्यतः कंप्यूटर एडेड डिजाइन(सीएडी), निर्माण(सीएएम) और अभियान्त्रिकी(सीएइ) में उपयोग किए जाते हैं। वे कई उद्योग-व्यापी मानकों का हिस्सा हैं, जैसे आईजीईएस, एसटीईपी, एसीआईएस और पीएचआईजीएस। एनयूआरबीएस सतहों को बनाने और संपादित करने के उपकरण विभिन्न 3D ग्राफिक्स और एनीमेशन सॉफ़्टवेयर पैकेजों में पाए जाते हैं। | |||
ये | ये कंप्यूटर क्रमादेश द्वारा कुशलता से देखे जा सकते हैं और आसानी से मानवीय संपर्क की अनुमति देते हैं। एनयूआरबीएस सतहें त्रि-आयामी क्षेत्र में एक सतह के लिए मानचित्रण दो मापदंडों के कार्य हैं। सतह का आकार नियंत्रण बिंदुओं द्वारा निर्धारित किया जाता है। एक सघन रूप में, एनयूआरबीएस सतहें सरल ज्यामितीय आकारों का प्रतिनिधित्व कर सकती हैं। जटिल जैविक आकृतियां के लिए टी- स्पलाइन और उपखंड सतहें अधिक उपयुक्त होती हैं क्योंकि वे एनयूआरबीएस की सतहों की तुलना में नियंत्रण बिंदुओं की संख्या को आधा कर देते हैं। | ||
सामान्य रूप से, NURBS वक्रों और सतहों का संपादन सहज और पूर्वानुमेय है।{{Citation needed|date=January 2021}} नियंत्रण बिंदु | सामान्य रूप से, NURBS वक्रों और सतहों का संपादन सहज और पूर्वानुमेय है।{{Citation needed|date=January 2021}}नियंत्रण बिंदु सदैव या तो सीधे वक्र या सतह से जुड़े होते हैं, या फिर रबर बैंड की तरह काम करते हैं। उपयोगकर्ता अंतरापृष्ठ के आधार पर, एनयूआरबीएस घटता और सतहों का संपादन उनके नियंत्रण बिंदुओं (बेज़ियर वक्र के समान) या उच्च स्तरीय उपकरण जैसे स्पलाइन प्रतिरुपण और श्रेणीबद्ध संपादन के माध्यम से हो सकता है। उपयोगकर्ता अंतरापृष्ठ के आधार पर एनयूआरबीएस वक्र और सतह के संपादन को उनके नियंत्रण बिन्दुओं (बेयर वक्र के सदृश) या उच्च स्तरीय उपकरणों के जरिए किया जा सकता है जैसे स्पलाइन प्रतिरुपण और श्रेणीबद्ध संपादन के माध्यम से हो सकता है।{{TOC limit|2}} | ||
== ऐतिहासिक पृष्ठभूमि == | == ऐतिहासिक पृष्ठभूमि == | ||
[[File:Spline (PSF).png|thumb|एक सपाट तख़्ता, | [[File:Spline (PSF).png|thumb|एक सपाट तख़्ता, स्पलाइन की एक भौतिक अभिव्यक्ति(गणित)]]कंप्यूटर से पहले, विभिन्न प्रारूपण उपकरणों के साथ डिजाइनों को हाथ से कागज पर तैयार किया जाता था। सीधी रेखाओं के लिए पटरी, वृत्तों के लिए दिशा निरूपण यंत्र(आलेखन) और कोणों के लिए चांदा का उपयोग किया जाता था। लेकिन कई आकृतियाँ, जैसे किसी जहाज के स्वतंत्र वक्र, इन उपकरणों से नहीं बनाया जा सकता था। चूँकि इस तरह के वक्र को आलेखन बोर्ड में मुक़्त रूप से खींचा जा सकता है, जहाज़ बनाने वालों को अधिकांशता एक यथार्थ आकार संस्करण की आवश्यकता होती थी जो हाथ से नहीं किया जा सकता था। इस तरह के बड़े चित्र लकड़ी की लचीली स्पलाइन की मदद से बनाए जाते थे, स्पलाइन को कई पूर्व निर्धारित बिंदुओं पर रखा गया था, जिन्हें डक्स कहा जाता था डक्स के बीच, स्पलाइन सामग्री की लोच ने स्पलाइन को आकार लेने का कारण बना दिया जिससे बंकन की ऊर्जा कम हो गई, और इस प्रकार बाधाओं के अनुरूप असुविधाजनक संभव आकार का निर्माण किया। डक्स को खिसका कर आकार को समायोजित किया जा सकता है।<ref name=mactech>{{cite web|last1=Schneider|first1=Philip|title=एनयूआरबी कर्व्स: ए गाइड फॉर द अनिनिशिएटेड|url=http://www.mactech.com/articles/develop/issue_25/schneider.html|website=MACTECH|access-date=26 September 2014}}</ref> | ||
1946 में, गणितज्ञों ने | |||
1946 में, गणितज्ञों ने स्पलाइन आकार का अध्ययन करना शुरू किया, और भाषा के अनुसमूह बहुपद सूत्र का प्रवेशन किया, जिसे स्पलाइन(गणित) या स्पलाइन फलन के रूप में जाना जाता है। आई.जे.स्कोनबर्ग ने ड्राफ्ट्समैन द्वारा उपयोग किए जाने वाले यांत्रिक स्पलाइन के समानता के बाद स्पलाइन फलन को अपना नाम दिया।<ref>{{cite journal | |||
|first = I. J. | |first = I. J. | ||
|last = Schoenberg | |last = Schoenberg | ||
| Line 24: | Line 25: | ||
|doi-access = free | |doi-access = free | ||
}}</ref> | }}</ref> | ||
चूंकि कंप्यूटर को डिजाइन की प्रक्रिया में सम्मिलित किया गया, ऐसे स्पलाइन के भौतिक गुणों की जांच की गई ताकि उन्हें गणितीय सटीकता के साथ प्रतिरूपित किया जा सके और जहां आवश्यक हो, पुन: प्रस्तुत किया जा सके। रेनॉल्ट अभियान्ता, पियरे बेज़ियर और सिट्रोएन के भौतिक विज्ञानी और गणितज्ञ पॉल डी कैस्टेलजौ द्वारा फ्रांस में अग्रणी कार्य किया था। उन्होंने लगभग एक दूसरे के समानांतर काम किया, लेकिन क्योंकि बेज़ियर ने अपने काम के परिणाम प्रकाशित किए, बेज़ियर वक्र का नाम उनके नाम पर रखा गया, जबकि डी कैस्टेलजौ का नाम संबंधित कलन विधि से जुड़ा है। | |||
रीयल-टाइम, एनयूआरबीएस | पहले एनयूआरबीएस का उपयोग केवल कार कंपनियों के मालिकाना(सीएडी) पैकेज में किया जाता था। बाद में वे मानक कंप्यूटर ग्राफिक्स पैकेज का हिस्सा बन गए। | ||
रीयल-टाइम, एनयूआरबीएस वक्र और सतहों का पारस्परिक प्रतिपादन पहली बार 1989 में सिलिकॉन ग्राफिक्स कार्यस्थल पर व्यावसायिक रूप से उपलब्ध कराया गया था। 1993 में, पीसीएस के लिए पहला पारस्परिक एनयूआरबीएस मॉडेलर, जिसे नोआरबीएस कहा जाता है, बर्लिन के तकनीकी विश्वविद्यालय के साथ सहयोग करने वाली एक छोटी सी कंपनी सीएएस बर्लिन द्वारा विकसित किया गया था। | |||
== निरंतरता == | == निरंतरता == | ||
{{Main| | {{Main| समतल फलन}} | ||
निर्माणाधीन एक सतह, के उदाहरण में एक मोटर याट का पतवार सामान्यतः कई एनयूआरबीएस सतहों से बना होता है जिन्हें एनयूआरबीएस पैच(या सिर्फ पैच) के रूप में जाना जाता है। इन सतह पैचों को इस तरह से एक साथ फिट किया जाता है कि सीमाएं अदृश्य हों। यह गणितीय रूप से ज्यामितीय परमापीय की अवधारणा द्वारा व्यक्त किया जाता है। | |||
ज्यामितीय | उच्च-स्तरीय उपकरण उपलब्ध हैं जो विभिन्न स्तरों की ज्यामितीय परमापीय बनाने और स्थापित करने के लिए एनयूआरबीएस की क्षमता से लाभान्वित होते हैं। | ||
* स्थितीय परमापीय(G<sup>0</sup>) संचालित करता है जब दो वक्रों या सतहों की अंतिम स्थिति संपाती होती है। वक्र या सतहें अभी भी एक कोण पर मिल सकते हैं, जो एक तेज कोने या किनारे को जन्म देती हैं और टूटी हुई झलकियाँ का कारण बनती हैं। | |||
* स्पर्शरेखा परमापीय(G¹) के लिए आवश्यक है कि वक्र या सतहों के अंत सदिश समानान्तर होते है और एक ही दिशा में, तेज किनारों को अस्वीकृत करते हैं। क्योंकि स्पर्शरेखीय रूप से निरंतर किनारे पर पड़ने वाले झलकियाँ सदैव निरंतर होती हैं और स्वाभाविक प्रतीत होता है कि परमापीय का यह स्तर प्रायः पर्याप्त हो सकता है। | |||
* वक्रता परमापीय(G²) के लिए अंत सदिशों की समान लंबाई और लंबाई परिवर्तन की दर की आवश्यकता होती है। वक्रता-निरंतर किनारे पर गिरने वाली झलकियाँ कोई भी परिवर्तन प्रदर्शित नहीं करती हैं, जिससे दो सतहें एक जैसी दिखाई देती हैं। यह देखने में पूर्णतया समतल है। परमापीय का यह स्तर उन मॉडलों के निर्माण में बहुत उपयोगी है जिनके लिए एक निरंतर सतह बनाने के लिए कई द्वि-घन पैच की आवश्यकता होती है। | |||
ज्यामितीय परमापीय मुख्य रूप से परिणामी सतह के आकार को संदर्भित करती है; चूँकि एनयूआरबीएस सतहें फलन करती हैं, और मापदंडों के संबंध में सतह के व्युत्पन्न पर वाद-विवाद करना संभव होता है। इसे प्राचलिक परमापीय के रूप में जाना जाता है। और किसी दिए गए मात्रा की प्राचलिक परमापीय का तात्पर्य उस मात्रा की ज्यामितीय परमापीय से होती है | |||
प्रथम- और द्वितीय-स्तर | प्रथम- और द्वितीय-स्तर प्राचलिक परमापीय(C0 और C¹) स्थितीय और स्पर्शरेखा(G0 और G¹) परमापीय के समान व्यावहारिक उद्देश्यों के लिए हैं। तृतीय-स्तरीय प्राचलिक परमापीय(C²), चूँकि, वक्रता परमापीय से अलग है क्योंकि इसका परमापीकरण भी निरंतर होता है। व्यवहार में, यदि समान बी- स्पलाइन का उपयोग किया जाता है तो C² का परमापीय प्राप्त करना आसान होता है। | ||
C<sup>''n''</sup> परमापीय की परिभाषा के लिए आवश्यक है कि सन्निकट वक्रों/सतहों का nवां व्युत्पन्न(<math>d^n C(u)/du^n</math>) जोड़ पर बराबर होते हैं।<ref>Foley, van Dam, Feiner & Hughes: ''[[Computer Graphics: Principles and Practice]]'', section 11.2, [[Addison-Wesley]] 1996 (2nd ed.).</ref> ध्यान दें कि वक्रों और सतहों के(आंशिक) व्युत्पन्न सदिश होते हैं जिनकी दिशा और परिमाण दोनों बराबर होते है। | |||
झलकियाँ और प्रतिबिंब उत्तम सपाटकरण को प्रकट करते हैं, जो कि एनयूआरबीएस सतहों के बिना प्राप्त करना व्यावहारिक रूप से असंभव है, जिसमें कम से कम G² परमापीय होता है। इस सिद्धांत का उपयोग सतह मूल्यांकन विधियों में से एक के रूप में किया जाता है जिससे किसी सतह की एक किरण का पता लगाया जाता है या उस पर प्रतिबिंबित होने वाली सफेद धारियों वाली छवि किसी सतह या सतहों के समुच्चय पर सबसे छोटे विचलन को भी दिखाती है। यह विधि कार प्रतिमान से ली गई है, जिसमें कार की सतह पर नियॉन-लाइट छत के प्रतिबिंबों की गुणवत्ता की जांच करके सतह की गुणवत्ता का निरीक्षण किया जाता है। इस पद्धति को ज़ेबरा विश्लेषण के रूप में जाना जाता है। | |||
== तकनीकी विनिर्देश == | == तकनीकी विनिर्देश == | ||
[[File:Surface modelling.svg|250px|right]]एक | [[File:Surface modelling.svg|250px|right]]एक एनयूआरबीएस वक्र को उसके क्रम, भारित नियंत्रण बिंदुओं के एक समुच्चय और एक समूह सदिश द्वारा परिभाषित किया गया है।<ref>{{cite book | ||
| title = बायो-इंस्पायर्ड सेल्फ-ऑर्गनाइजिंग रोबोटिक सिस्टम्स| url = https://www.springer.com/engineering/computational+intelligence+and+complexity/book/978-3-642-20759-4 | | title = बायो-इंस्पायर्ड सेल्फ-ऑर्गनाइजिंग रोबोटिक सिस्टम्स| url = https://www.springer.com/engineering/computational+intelligence+and+complexity/book/978-3-642-20759-4 | ||
| access-date = 2014-01-06 | | access-date = 2014-01-06 | ||
| page = 9 | | page = 9 | ||
}}</ref> | }}</ref> एनयूआरबीएस वक्र और सतहें बी- स्पलाइन और बेज़ियर वक्रों और सतहों दोनों का सामान्यीकरण हैं, प्राथमिक अंतर नियंत्रण बिंदुओं का भार है, जो एनयूआरबीएस वक्रो को तर्कसंगत बनाता है। गैर- परिमय, अन्य सरल, बी- स्पलाइन का एक विशेष स्थिति का सब समुच्चय है, जहां प्रत्येक नियंत्रण बिंदु एक समांगी निर्देशांक के अतिरिक्त एक नियमित गैर-समरूप समन्वय 'डब्ल्यू' है।<ref>{{cite web|url=https://www.cl.cam.ac.uk/teaching/2000/AGraphHCI/SMEG/node5.html|title=वाजिब बी-splines|website=www.cl.cam.ac.uk}}</ref> यह प्रत्येक नियंत्रण बिंदु पर वजन 1 होने के बराबर है, पर्याप्त बी- स्पलाइन प्रत्येक नियंत्रण बिंदु के 'w' भार के रूप में उपयोग करते हैं।<ref>{{cite web|url=https://www.cs.mtu.edu/~shene/COURSES/cs3621/NOTES/spline/NURBS/NURBS-def.html|title=NURBS: परिभाषा|website=www.cs.mtu.edu}}</ref>) | ||
नियंत्रण बिंदुओं के | |||
नियंत्रण बिंदुओं के दो विमीय जाल का उपयोग करके, समतल पैच और गोले के वर्गों सहित एनयूआरबीएस सतहों को बनाया जा सकता है। इन्हें सामान्यतः एस टी या यू वी नामक दो चर के साथ परमापीकरण किया जाता है। इसे एनयूआरबीएस प्रतिचित्रण <math>\mathbb{R}^n\to \mathbb{R}^n</math> बनाने के लिए यादृच्छिक विमा तक बढ़ाया जा सकता है। | |||
एनयूआरबीएस वक्र और सतहें कई कारणों से उपयोगी हैं। | |||
* किसी दिए गए क्रम के लिए | * किसी दिए गए क्रम के लिए एनयूआरबीएस का समुच्चय सजातीय रूपांतरण के तहत अपरिवर्तनीय होता है।<ref>David F. Rogers: An Introduction to NURBS with Historical Perspective, section 7.1</ref> घूर्णन और परिक्रमणहीन एक समान गतिविधि जैसे संचालनों को उनके नियंत्रण बिंदुओं पर लागू करके एनयूआरबीएस वक्रों और सतहों पर लागू किया जा सकता है। | ||
* वे मानक विश्लेषणात्मक आकृतियों (जैसे, शांकव) और मुक्त-रूप आकृतियों दोनों के लिए एक सामान्य गणितीय रूप प्रदान करते हैं। | * वे मानक विश्लेषणात्मक आकृतियों(जैसे, शांकव) और मुक्त-रूप आकृतियों दोनों के लिए एक सामान्य गणितीय रूप प्रदान करते हैं। | ||
* वे विभिन्न प्रकार की आकृतियों को डिजाइन करने के लिए लचीलापन प्रदान करते हैं। | * वे विभिन्न प्रकार की आकृतियों को डिजाइन करने के लिए लचीलापन प्रदान करते हैं। | ||
* वे आकृतियों को संग्रहीत करते समय | * वे आकृतियों को संग्रहीत करते समय स्मरण शक्ति की ज़रूरत,को कम करते हैं(सरल तरीकों की तुलना में)। | ||
* संख्यात्मक रूप से स्थिर और सटीक | * संख्यात्मक रूप से स्थिर और सटीक कलन विधि द्वारा उनका यथोचित शीघ्रता से मूल्यांकन किया जाता है। | ||
यहाँ, | यहाँ, एनयूआरबीएस अधिकतर एक विमीय वक्र में होता है, इसे दो सतहों या अधिक विमा के लिए सामान्यीकृत किया जा सकता है। | ||
=== | === क्रम === | ||
एनयूआरबीएस वक्र का क्रम पास के नियंत्रण बिंदुओं की संख्या को परिभाषित करता है जो वक्र पर किसी दिए गए बिंदु को प्रभावित करते हैं। वक्र को वक्र के क्रम से एक कोटि कम के बहुपद द्वारा गणितीय रूप से दर्शाया जाता है। इसलिए, दूसरे क्रम के वक्र को रैखिक वक्र कहा जाता है(जो रैखिक बहुपदों द्वारा दर्शाए जाते हैं), तीसरे क्रम के वक्र को द्विघात वक्र कहा जाता है, और चौथे क्रम के वक्र को घन वक्र कहा जाता है। नियंत्रण बिंदुओं की संख्या वक्र के क्रम से अधिक या उसके बराबर होनी चाहिए। | |||
प्रयोग में, क्यूबिक वक्र सबसे अधिक उपयोग किए जाने वाले हैं। पांचवें और छठे क्रम के वक्र कभी-कभी उपयोगी होते हैं, विशेष रूप से निरंतर उच्च क्रम के व्युत्पन्न प्राप्त करने के लिए है, लेकिन उच्च क्रम के वक्रों का व्यावहारिक रूप से कभी उपयोग नहीं किया जाता है। क्योंकि वे आंतरिक संख्यात्मक समस्याओं का कारण बनते हैं और असमान रूप से बड़ी गणना समय की आवश्यकता होती है। | |||
=== नियंत्रण बिंदु === | === नियंत्रण बिंदु === | ||
[[File:NURBS 3-D surface.gif|250px|thumb|त्रि-आयामी | [[File:NURBS 3-D surface.gif|250px|thumb|त्रि-आयामी एनयूआरबीएस सतहों में जटिल, जैविक आकार हो सकते हैं। नियंत्रण बिंदु सतह की दिशाओं को प्रभावित करते हैं। नियंत्रण पिंजरे के नीचे एक अलग वर्ग सतह के एक्स और वाई विस्तार को चित्रित करता है।]]नियंत्रण बिंदु वक्र के आकार को निर्धारित करते हैं।<ref>{{cite book |last=Gershenfeld |first=Neil |author-link=Neil Gershenfeld |year=1999 |page=141 |title=गणितीय मॉडलिंग की प्रकृति|publisher=[[Cambridge University Press]] |isbn=0-521-57095-6}}</ref> सामान्यतः, वक्र के प्रत्येक बिंदु की गणना कई नियंत्रण बिंदुओं का भारित योग करके की जाती है। प्रत्येक बिंदु का वजन शासकीय मापदण्ड के अनुसमूह भिन्न होता है। कोटि डी के वक्र के लिए, मापदण्ड के क्षेत्र डी + 1 अंतराल में किसी भी नियंत्रण बिंदु का वजन केवल गैर-शून्य होता है। उन अंतरालों के भीतर, कोटि डी के बहुपद फलन(आधार फलन) के अनुसमूह वजन बदलता है। और अंतराल की सीमाओं पर, आधार फलन सुचारू रूप से बहुपद की कोटि द्वारा निर्धारित किया जाता है और समतलता शून्य करने के लिए जाना जाता है। | ||
एक उदाहरण के रूप में, कोटि का आधार फलन त्रिकोण फलन होता है। यह शून्य से 1 तक बढ़ता है, फिर शून्य पर गिर जाता है। जब यह बढ़ता है, तो पिछले नियंत्रण बिंदु का आधार फलन गिरता है। इस प्रकार, वक्र दो बिंदुओं के बीच प्रक्षेपित होता है और परिणामी वक्र एक बहुभुज होता है, जो निरंतर, लेकिन अंतराल सीमाओं या समूह पर भिन्न नहीं होता है।.उच्च कोटि के बहुपदों में संगत रूप से अधिक अविच्छिन्न क्षेत्र होते हैं। ध्यान दें कि अंतराल के भीतर आधार फलन की बहुपद प्रकृति और निर्माण की रैखिकता वक्र को पूरी तरह समतल बनाती है, इसलिए केवल समूहों पर ही विच्छिन्नता उत्पन्न हो सकती है। | |||
उदाहरण के | |||
कई अनुप्रयोगों में तथ्य यह है कि एक एकल नियंत्रण बिंदु केवल उन अंतरालों को प्रभावित करता है जहां यह सक्रिय है, एक अत्यधिक वांछनीय गुण है, जिसे 'स्थानीय समर्थन' के रूप में जाना जाता है। | कई अनुप्रयोगों में तथ्य यह है कि एक एकल नियंत्रण बिंदु केवल उन अंतरालों को प्रभावित करता है जहां यह सक्रिय होता है, एक अत्यधिक वांछनीय गुण है, जिसे 'स्थानीय समर्थन' के रूप में जाना जाता है। प्रतिरूपण में, यह अन्य भागों को अपरिवर्तित रखते हुए सतह के एक हिस्से को बदलने की अनुमति देता है। | ||
अधिक नियंत्रण बिंदुओं को जोड़ने से किसी दिए गए वक्र के लिए बेहतर सन्निकटन की अनुमति मिलती है, | अधिक नियंत्रण बिंदुओं को जोड़ने से किसी दिए गए वक्र के लिए बेहतर सन्निकटन की अनुमति मिलती है, यद्यपि वक्रों का एक निश्चित वर्ग को नियंत्रण बिंदुओं की सीमित संख्या के साथ सटीक रूप से प्रदर्शित किया जा सकता है। एनयूआरबीएस वक्र में प्रत्येक नियंत्रण बिंदु के लिए एक अदिश भार होता है। यह नियंत्रण बिंदुओं की संख्या को अनावश्यक रूप से बढ़ाए बिना वक्र के आकार पर अधिक नियंत्रण की अनुमति देता है। विशेष रूप से, यह वक्रों के समुच्चय में वृत्तो और दीर्घवृत्त जैसे शंकु वर्गों को जोड़ता है जिन्हें सटीक रूप से प्रदर्शित किया जा सकता है। एनयूआरबीएस में तर्कसंगत शब्द इन भारों को को दर्शाता है। | ||
नियंत्रण बिंदुओं में कोई भी | नियंत्रण बिंदुओं में कोई भी विमीय हो सकता है। एक-विमीय बिंदु केवल मापदण्ड के अदिश(गणित) फलन को परिभाषित करते हैं। सामान्यतया इनका उपयोग प्रतिबिंब संसाधन फलन में चमक और रंग वक्रो को समायोजित करने के लिए किया जाता है। 3डी प्रतिरूपण में त्रि-विमीय नियंत्रण बिंदुओं का बहुलता से प्रयोग किए जाते हैं, जहाँ हर प्रकार के 3 डी क्षेत्र में "बिंदु" शब्द के प्रत्येक अर्थ में उनका प्रयोग किया जाता है। | ||
समय-चालित मूल्यों के | समय-चालित मूल्यों के समुच्चय को नियंत्रित करने के लिए बहु-विमीय बिंदुओं का उपयोग किया जा सकता है, उदाहरण के लिए एक रोबोट भुजा की विभिन्न स्थितीय और घूर्णी समुच्चय, एनयूआरबीएस सतहें का एक अनुप्रयोग हैं। प्रत्येक नियंत्रण 'बिंदु' वास्तव में वक्र को परिभाषित करते हुए नियंत्रण बिंदुओं का एक पूर्ण सदिश है। ये वक्र अपनी कोटि और नियंत्रण बिंदुओं की संख्या साझा करते हैं, और मापदंड के क्षेत्र एक विमीय को फैलाते हैं। मापदंड क्षेत्र के दूसरे विमीय पर इन नियंत्रण सदिश को प्रक्षेपित करके, वक्रों का एक सतत समुच्चय प्राप्त किया जाता है, जो सतह को परिभाषित करता है। | ||
=== | === समूह सदिश === | ||
समूह सदिश, मापदंड मानों का एक अनुक्रम होता है, जो यह निर्धारित करता है कि नियंत्रण बिंदु कहां और कैसे एनयूआरबीएस वक्र को प्रभावित करते हैं। समूह की संख्या सदैव नियंत्रण बिंदुओं की संख्या प्लस वक्र की कोटि प्लस वन के बराबर होती है,(जैसे नियंत्रण बिंदुओं की संख्या और वक्र क्रम के बराबर होते है)। समूह सदिश पहले उल्लेखित अंतराल में प्राचलिक क्षेत्र को विभाजित करता है, जिसे सामान्यतया समूह अवधि के नाम से जाना जाता है। प्रत्येक बार मापदण्ड मान एक नए समूह विस्तार में प्रवेश करता है, एक नया नियंत्रण बिंदु सक्रिय हो जाता है, जबकि एक पुराने नियंत्रण बिंदु को त्याग दिया जाता है। यह निम्नानुसमूह है कि समूह सदिश में मान गैर-घटते क्रम में होना चाहिए, इसलिए(0, 0, 1, 2, 3, 3) मान्य है जबकि(0, 0, 2, 1, 3, 3) नहीं है। | |||
यह | |||
क्रमिक | क्रमिक समूह का समान मूल्य हो सकता है। यह तब शून्य लंबाई के समूह अवधि को परिभाषित करता है, जिसका अर्थ है कि दो नियंत्रण बिंदु एक ही समय में सक्रिय होते हैं(और निश्चित रूप से दो नियंत्रण बिंदु निष्क्रिय हो जाते हैं)। इसका परिणामी वक्र या इसके उच्च व्युत्पन्नों की परमापीय पर प्रभाव पड़ता है, उदाहरण के लिए, यह एक अन्य समतल एनयूआरबीएस वक्र में कोनों के निर्माण की अनुमति देता है। | ||
कई संयोगी | कई संयोगी समूह को कभी-कभी एक निश्चित 'बहुलता' वाली समूह के रूप में संदर्भित किया जाता है। दो या तीन की बहुलता वाली समूह को दोहरी या तिहरी समूह कहा जाता है। समूह की बहुलता वक्र की कोटि तक सीमित होती है, चूँकि एक उच्च बहुलता वक्र को अलग-अलग भागों में विभाजित कर देगी और यह नियंत्रण बिंदुओं को अप्रयुक्त छोड़ देगी। प्रथम-कोटि एनयूआरबीएस के लिए, प्रत्येक समूह को एक नियंत्रण बिंदु के साथ जोड़ा जाता है। | ||
समूह सदिश सामान्यतः एक समूह से शुरू होता है जिसमें बहुलता क्रम के बराबर होती है। यह समझ में आता है, क्योंकि यह उन नियंत्रण बिंदुओं को सक्रिय करता है जिनका प्रभाव पहली समूह की अवधि पर पड़ता है। इसी तरह, समूह सदिश सामान्यतः उस बहुलता की समूह के साथ समाप्त होता है। | |||
ऐसे | ऐसे समूह सदिश वाले वक्र एक नियंत्रण बिंदु पर शुरू और समाप्त होते हैं। | ||
समूह के मान निविष्टि मापदण्ड और संबंधित एनयूआरबीएस मान के बीच मानचित्रण को नियंत्रित करते हैं। उदाहरण के लिए, यदि एनयूआरबीएस क्षेत्र के माध्यम से किसी पथ का वर्णन करती है, तो समूह उस समय को नियंत्रित करती हैं जब फलन नियंत्रण बिंदुओं से आगे बढ़ता है। आकृतियों का प्रतिनिधित्व करने के प्रयोजनों के लिए, चूँकि, समूह मूल्यों के बीच के अंतर का अनुपात ही महत्व रखता है, उस स्थिति में, समूह सदिश(0, 0, 1, 2, 3, 3) और(0, 0, 2, 4, 6, 6) समान वक्र उत्पन्न करते हैं। समूह मूल्यों की स्थिति मापदण्ड क्षेत्रौ के मानचित्रण को वक्र क्षेत्र पर प्रभावित करती है। एक एनयूआरबीएस वक्र का प्रतिपादन सामान्यतः मापदण्ड रेंज के माध्यम से एक निश्चित कदम के साथ किया जाता है। समूह अवधि की लंबाई बदलकर, क्षेत्रों में प्रतिरूप बिंदुओं का उपयोग किया जा सकता है, जहां वक्रता अधिक होती है। एक अन्य उपयोग उन स्थितियों में होता है जहां मापदण्ड मान का कुछ भौतिक महत्व होता है, उदाहरण के लिए यदि मापदण्ड समय है और वक्र एक रोबोट भुजा की गति का वर्णन करता है। समूह की लंबाई फिर वेग और त्वरण में तब्दील हो जाती है, जो रोबोट के भुजा या उसके पर्यावरण को नुकसान से बचाने के लिए सही पाने के लिए आवश्यक हैं। मानचित्रण में यह लचीलापन है जो एनयूआरबीएस में गैर-समान वाक्यांश को संदर्भित करता है। | |||
केवल आंतरिक | केवल आंतरिक गणना के लिए ही आवश्यक है, समूह सामान्यतः प्रतिरूपण सॉफ़्टवेयर के उपयोगकर्ताओं के लिए सहायक नहीं होते हैं। इसलिए, कई प्रतिरूपण अनुप्रयोग समूह को संपादन योग्य या यहां तक कि दृश्यमान नहीं बनाते हैं। नियंत्रण बिंदुओं में भिन्नता को देखकर सामान्यतः उचित समूह सदिश स्थापित करना संभव होता है। एनयूआरबीएस सॉफ़्टवेयर के नवीनतम संस्करण संस्करण(जैसे, ऑटोडेस्क माया और गैंडा 3D) समूह की स्थिति के पारस्परिक संपादन की अनुमति देते हैं, लेकिन यह नियंत्रण बिंदुओं के संपादन की तुलना में काफी कम सहज ज्ञान युक्त होते है। | ||
=== आधार | === आधार फलनों का निर्माण === | ||
एनयूआरबीएस वक्रों के निर्माण में उपयोग किए जाने वाले B- स्पलाइन आधार फलनों को सामान्यतः <math>N_{i,n}(u)</math> से चिह्नित किया जाता है, जिसमें <math>i</math> के अनुरूप कार्य होता है, और <math>i</math><sup>वें</sup> नियंत्रण बिंदु, और <math>n</math> आधार फलन की कोटि साथ मेल खाती है।<ref name=nurbs-book>{{cite book |last1=Piegl |first1=Les |last2=Tiller |first2=Wayne |title=द एनयूआरबीएस बुक|date=1997 |publisher=Springer |location=Berlin |isbn=3-540-61545-8 |edition=2. |url-access=registration |url=https://archive.org/details/nurbsbook00pieg }}</ref> मापदण्ड निर्भरता को सदैव छोड़ दिया जाता है, इसलिए हम <math>N_{i,n}</math>.लिख सकते हैं, इन आधार फलनों की परिभाषा <math>n</math> में पुनरावर्ती है कोटि -0 फलन <math>N_{i,0}</math> टुकड़े-टुकड़े में स्थिर फलन हैं। वे संबंधित समूह अवधि पर एक हैं और हर जगह शून्य हैं। प्रभावी रूप से, <math>N_{i,n}</math> का एक रैखिक प्रक्षेप है <math>N_{i,n-1}</math> तथा <math>N_{i+1,n-1}</math>. बाद के दो फलन <math>n</math> समूह विस्तार के लिए गैर-शून्य हैं, <math>n-1</math> समूह विस्तार के लिए अतिव्यापन होते है। फलन <math>N_{i,n}</math> की गणना | |||
नियंत्रण बिंदु, और <math>n</math> आधार | |||
इन आधार | |||
प्रभावी रूप से, <math>N_{i,n}</math> का एक रैखिक प्रक्षेप है <math>N_{i,n-1}</math> तथा <math>N_{i+1,n-1}</math>. बाद के दो | |||
<math>n</math> | |||
[[File:nurbsbasisconstruct.svg|thumb|ऊपर से नीचे तक: रैखिक आधार | [[File:nurbsbasisconstruct.svg|thumb|ऊपर से नीचे तक: रैखिक आधार फलन <math>N_{1,1}</math>(नीला) और <math>N_{2,1}</math>(हरा)(शीर्ष),उनके भार फलन <math>f</math> और <math>g</math> के बीच में होते हैं और परिणामी द्विघात आधार फलन के नीचे समूह होती हैं0, 1, 2 और 2.5 हैं]]: <math>N_{i,n} = f_{i,n} N_{i,n-1} + g_{i+1,n} N_{i+1,n-1}</math> के रूप में की जाती है | ||
<math>f_i</math> | <math>f_i</math> रैखिक रूप से अंतराल शून्य से एक तक बढ़ता है जहां <math>N_{i,n-1}</math> गैर-शून्य है, जबकि <math>g_{i+1}</math> अंतराल पर एक से शून्य तक गिर जाता है जहां <math>N_{i+1,n-1}</math> गैर-शून्य है। जैसा पहले बताया गया है, <math>N_{i,1}</math> एक त्रिकोणीय फलन है, पहले पर शून्य से एक तक बढ़ते हुए दो समूह विस्तार पर अशून्य, और दूसरी समूह अवधि पर शून्य तक गिरना। उच्च क्रम के आधार फलन गैर-शून्य होते हैं जो कि अधिक समूह फैलाव के अनुरूप होते हैं और इसके अनुरूप उच्च कोटि होती है। यदि <math>u</math> मापदण्ड है, और <math>k_i</math>के <math>i</math><sup>वें समूह है तथा इन्हे हम फलन f और g के रूप में लिख सकते हैं। | ||
: <math>f_{i,n}(u) = {{u - k_i} \over {k_{i+n} - k_i}}</math> | : <math>f_{i,n}(u) = {{u - k_i} \over {k_{i+n} - k_i}}</math> | ||
| Line 112: | Line 107: | ||
: <math>g_{i,n}(u) = 1 - f_{i,n}(u) = {{k_{i+n} - u} \over {k_{i+n} - k_{i}}}</math> | : <math>g_{i,n}(u) = 1 - f_{i,n}(u) = {{k_{i+n} - u} \over {k_{i+n} - k_{i}}}</math> | ||
फलन <math>f</math> तथा <math>g</math> धनात्मक होते हैं जब संगत निचले क्रम के आधार फलन गैर-शून्य होते हैं। n पर गणितीय आगमन से यह पता चलता है कि के सभी मानों के लिए आधार फलन <math>n</math> तथा <math>u</math> गैर-ऋणात्मक होते है, यह आधार फलन की गणना को संख्यात्मक रूप से स्थिर बनाता है। | |||
फिर से प्रेरण द्वारा, यह साबित किया जा सकता है कि | फिर से प्रेरण द्वारा, यह साबित किया जा सकता है कि मापदण्ड के किसी विशेष मान के लिए आधार फलनों का योग एकात्मकता होती है। इसे आधार फलनों के एकात्मकता गुण के विभाजन के रूप में जाना जाता है। | ||
[[File:nurbsbasislin2.png|frame|रैखिक आधार | [[File:nurbsbasislin2.png|frame|रैखिक आधार फलन]] | ||
[[File:nurbsbasisquad2.png|frame|द्विघात आधार | [[File:nurbsbasisquad2.png|frame|द्विघात आधार फलन]]आंकड़े समूह के लिए रैखिक और द्विघात आधार फलनों को दिखाते हैं {..., 0, 1, 2, 3, 4, 4.1, 5.1, 6.1, 7.1, ...} | ||
एक | एक समूह विस्तार अन्य की तुलना में काफी कम होता है। उस समूह की अवधि पर, द्विघात आधार फलन में में शिखर अधिक विशिष्ट है, लगभग एक तक पहुँचने के विपरीत, निकटवर्ती आधार फलन अधिक तेज़ी से शून्य हो जाते हैं। ज्यामितीय व्याख्या में, इसका मतलब है कि वक्र संबंधित नियंत्रण बिंदु के करीब पहुंचता है। एक डबल समूह के स्थिति में, समूह अवधि की लंबाई शून्य हो जाती है और शिखर एक तक पहुँच जाता है। आधार फलन अब उस बिंदु पर भिन्न नहीं है। यदि निकटतम नियंत्रण बिंदु समरेख नहीं हैं '''तो वक्र पर नुकीला कोना होगा।''' | ||
=== एक | === एक एनयूआरबीएस वक्र का सामान्य रूप === | ||
आधार | आधार फलनों की परिभाषाओं का उपयोग करना <math>N_{i,n}</math> पिछले अनुच्छेद से, एक एनयूआरबीएस वक्र निम्न रूप लेता है<ref name="nurbs-book" /> | ||
: <math>C(u) = \sum_{i=1}^{k} {\frac | : <math>C(u) = \sum_{i=1}^{k} {\frac | ||
| Line 133: | Line 128: | ||
{\sum_{i=1}^k {N_{i,n}(u)w_i}} | {\sum_{i=1}^k {N_{i,n}(u)w_i}} | ||
</math> | </math> | ||
इसमें, <math>k</math> नियंत्रण बिंदुओं की संख्या है <math>\mathbf{P}_i</math> तथा <math>w_i</math> संगत भार हैं। भाजक एक सामान्य कारक है जो एक का मूल्यांकन करता है यदि सभी भार एक हैं। इसे आधार | इसमें, <math>k</math> नियंत्रण बिंदुओं की संख्या है <math>\mathbf{P}_i</math> तथा <math>w_i</math> संगत भार हैं। भाजक एक सामान्य कारक है जो एक का मूल्यांकन करता है यदि सभी भार एक हैं। और इसे आधार फलनों की एकात्मकता गुण के विभाजन के रूप में देखा जाता है। इसे इस रूप में लिखने की प्रथा है | ||
: <math>C(u)=\sum_{i=1}^k R_{i,n}(u)\mathbf{P}_i</math> | : <math>C(u)=\sum_{i=1}^k R_{i,n}(u)\mathbf{P}_i</math> | ||
जिसमें | जिसमें फलन को, | ||
: <math>R_{i,n}(u) = {N_{i,n}(u)w_i \over \sum_{j=1}^k N_{j,n}(u)w_j}</math> | : <math>R_{i,n}(u) = {N_{i,n}(u)w_i \over \sum_{j=1}^k N_{j,n}(u)w_j}</math> | ||
परिमेय आधार फलन के रूप में जाना जाता है। | |||
=== एक | === एक एनयूआरबीएस सतह का सामान्य रूप === | ||
एक | एक एनयूआरबीएस सतह को दो एनयूआरबीएस वक्रों के प्रदिश गुणनफल के रूप में प्राप्त किया जाता है, इस प्रकार दो स्वतंत्र मापदंडों का उपयोग किया जाता है <math>u</math> तथा <math>v</math> सूचकांक के साथ <math>i</math> तथा <math>j</math> क्रमश <ref name="nurbs-book" /> | ||
: <math>S(u,v) = \sum_{i=1}^k \sum_{j=1}^l R_{i,j}(u,v) \mathbf{P}_{i,j} </math> | : <math>S(u,v) = \sum_{i=1}^k \sum_{j=1}^l R_{i,j}(u,v) \mathbf{P}_{i,j} </math> | ||
| Line 149: | Line 144: | ||
: <math>R_{i,j}(u,v) = \frac {N_{i,n}(u) N_{j,m}(v) w_{i,j}} {\sum_{p=1}^k \sum_{q=1}^l N_{p,n}(u) N_{q,m}(v) w_{p,q}}</math> | : <math>R_{i,j}(u,v) = \frac {N_{i,n}(u) N_{j,m}(v) w_{i,j}} {\sum_{p=1}^k \sum_{q=1}^l N_{p,n}(u) N_{q,m}(v) w_{p,q}}</math> | ||
तर्कसंगत आधार | तर्कसंगत आधार फलनों के रूप में होता है। | ||
=== | == एनयूआरबीएस वस्तुओं में हेरफेर करना == | ||
जैसा कि शब्द से पता चलता है, | [[File:motoryacht design i.png|thumb|250px|right|एनयूआरबीएस सतहों का उपयोग करके मोटरयाट डिज़ाइन बनाते है]]कई रूपांतरणों को एक एनयूआरबीएस वस्तु पर लागू किया जा सकता है। उदाहरण के लिए, यदि वक्र को एक निश्चित कोटि और N नियंत्रण बिंदुओं के उपयोग से परिभाषित किया जाता है, तो वक्र को कोटि और N+1 नियंत्रण बिंदुओं का उपयोग करते हुए व्यक्त किया जा सकता है। इस प्रक्रिया में कई नियंत्रण बिंदु स्थिति को बदलते हैं और समूह सदिश में एक समूह अन्तर्स्थापित की जाती है। पारस्परिक डिज़ाइन के दौरान इन परिचालन का बड़े पैमाने पर उपयोग किया जाता है। नियंत्रण बिंदु जोड़ते समय, वक्र का आकार वही रहना चाहिए, जिससे आगे के समायोजन के लिए शुरुआती बिंदु बन सके। इनमें से कई संक्रिया पर नीचे चर्चा की गई है।<ref name="nurbs-book" /><ref>{{cite journal | last1 = Piegl | first1 = L. | year = 1989| title = तर्कसंगत बी-स्प्लिन के आकार को संशोधित करना। भाग 1: घटता है| journal = Computer-Aided Design | volume = 21 | issue = 8| pages = 509–518 | doi = 10.1016/0010-4485(89)90059-6 }}</ref> | ||
=== समूह सम्मिलन === | |||
जैसा कि शब्द से पता चलता है, समूह सम्मिलन समूह सदिश में एक समूह सम्मिलित करता है। यदि वक्र की कोटि <math>n</math> है, तो <math>n-1</math> नियंत्रण बिंदुओं को <math>n</math> द्वारा प्रतिस्थापित किया जाता है और एक नए वक्र का आकार समान रहता है। | |||
एक समूह की अधिकतम बहुलता, को कई बार अन्तर्निविष्ट किया जाता है। इसे कभी-कभी समूह शोधन के रूप में संदर्भित किया जाता है और इसे एक कलां विधि द्वारा प्राप्त किया जा सकता है जो बार-बार समूह सम्मिलन की तुलना में अधिक कुशल होते है। | |||
=== | === समूह हटाना === | ||
समूह हटाना समूह सम्मिलन का उल्टा है। इसका उद्देश्य अधिक सघन प्रतिनिधित्व प्राप्त करने के लिए समूह और संबंधित नियंत्रण बिंदुओं को हटाना है। स्पष्ट है कि वक्र की सही आकृति को बनाए रखते हुए यह सदैव संभव नहीं होता है। व्यवहार में, सटीकता में सहिष्णुता का उपयोग यह निर्धारित करने के लिए किया जाता है कि क्या समूह को हटाया जा सकता है। प्रक्रिया का उपयोग एक पारस्परिक सत्र के बाद परिशोधन के लिए किया जाता है जिसमें नियंत्रण बिंदुओं को हस्तचालित रूप से या प्राप्त करने के बाद जोड़ा जा सकता है, जहां एक सीधी रूपांतरण प्रक्रिया निरर्थक नियंत्रण बिंदुओं की ओर ले जाती है | |||
=== | === कोटि उन्नयन === | ||
किसी विशेष | किसी विशेष कोटि के एनयूआरबीएस वक्र को सदैव उच्च कोटि के एनयूआरबीएस वक्र द्वारा दर्शाया जाता है। अलग-अलग एनयूआरबीएस वक्र को जोड़ते समय इसका अधिकांशता उपयोग किया जाता है, उदाहरण के लिए, एनयूआरबीएस वक्र के एक समुच्चय के बीच एनयूआरबीएस सतह बनाते समय या आसन्न वक्र को एकीकृत करता है। प्रक्रिया में, विभिन्न वक्रों को एक ही कोटि तक लाया जाना चाहिए, अधिकांशता वक्रों के समुच्चय की अधिकतम कोटि होती है, इस प्रक्रिया को कोटि ऊंचाई के रूप में जाना जाता है। | ||
उदाहरण के लिए, | |||
=== वक्रता === | === वक्रता === | ||
विभेदक ज्यामिति में सबसे महत्वपूर्ण गुण वक्रता | विभेदक ज्यामिति में सबसे महत्वपूर्ण गुण वक्रता <math>\kappa</math>.है, यह स्थानीय गुण किनारों, कोनों आदि का वर्णन करता है। और पहली और दूसरी व्युत्पन्न के बीच संबंधों का वर्णन करता है, और इस प्रकार, सटीक वक्र आकार का वर्णन करता है। अवकलज निर्धारित करने के बाद गणना करना आसान है <math>\kappa=\frac{|r'(t) \times r''(t)|}{|r'(t)|^3}</math> या दूसरे व्युत्पन्न से चाप की लम्बाई के रूप में अनुमानित <math>\kappa=|r''(s_o)|</math>.करता है। और वक्रता की सीधी गणना <math>\kappa</math> इन समीकरणों के साथ उनके बहुभुज अभ्यावेदन के विरुद्ध परिचालित वक्रों का बड़ा लाभ है। | ||
== उदाहरण: एक वृत्त == | == उदाहरण: एक वृत्त == | ||
[[File:NURBS-circle-3D.svg|thumb|300px| | [[File:NURBS-circle-3D.svg|thumb|300px|एनयूआरबीएस के पास वृत्तो का सटीक वर्णन करने की क्षमता है। यहाँ, काला त्रिभुज एक एनयूआरबीएस वक्र का नियंत्रण बहुभुज है(w=1 पर दिखाया गया है)। नीली बिंदीदार रेखा 3डी सजातीय निर्देशांक में बी- स्पलाइन वक्र के संबंधित नियंत्रण बहुभुज को दर्शाती है, जो संबंधित वजन द्वारा नियंत्रण बिंदुओं द्वारा एनयूआरबीएस को गुणा करके बनाई गई है। नीले परवलय 3डी में संगत बी- स्पलाइन वक्र हैं, जिसमें तीन परवलय होते हैं। एनयूआरबीएस नियंत्रण बिंदुओं और भारों का चयन करके, परवलय भूरा शंकु के विपरीत फलक के समानांतर होते हैं(3D मूल पर इसकी नोक के साथ), इसलिए परवलय को w = 1 तल पर प्रक्षेपित करने के लिए w से विभाजित करने से वृत्ताकार चाप बनते हैं(लाल वृत्त; शंकु खंड देखें)।]]गैर-परिमय स्पलाइन या बेज़ियर वक्र एक वृत्त का अनुमान लगा सकते हैं, लेकिन वे इसका सटीक रूप से प्रतिनिधित्व नहीं कर सकते। परिमय स्पलाइन किसी भी शंकु खंड का प्रतिनिधित्व कर सकते हैं, जिनमें वृत्त भी सम्मिलित होते है, यह प्रतिनिधित्व अद्वितीय नहीं है, परंतु एक संभावना नीचे दिखाई देती है। | ||
{| class="wikitable" style="margin:1em auto; text-align: center" | {| class="wikitable" style="margin:1em auto; text-align: center" | ||
! style="width:6em;" | ''x'' | ! style="width:6em;" | ''x'' | ||
! style="width:6em;" | ''y'' | ! style="width:6em;" | ''y'' | ||
! style="width:6em;" | ''z'' | ! style="width:6em;" | ''z'' | ||
! style="width:6em;" | | ! style="width:6em;" | भार | ||
|- | |- | ||
| 1 || 0 || 0 || 1 | | 1 || 0 || 0 || 1 | ||
| Line 198: | Line 188: | ||
| 1 || 0 || 0 || 1 | | 1 || 0 || 0 || 1 | ||
|} | |} | ||
क्रम तीन है, क्योंकि एक वृत्त एक द्विघात वक्र है और | क्रम तीन है, क्योंकि एक वृत्त एक द्विघात वक्र है और स्पलाइन का क्रम इसके टुकड़े वार बहुपद खंडों की कोटि से एक अधिक है। समूह सदिश है <math>\{0, 0, 0, \pi/2, \pi/2, \pi, \pi, 3\pi/2, 3\pi/2, 2\pi, 2\pi, 2\pi\}\,</math>वृत्त चार चौथाई वृत्तों से बना होता है जो दोहरे समूह के साथ बंधे होते हैं। चूँकि, तीसरे क्रम में डबल समूह एनयूआरबीएस वक्र सामान्य रूप से पहले अवकलज में निरंतरता के नुकसान का परिणाम होता है, नियंत्रण बिंदु इस तरह से स्थित हैं कि पहला व्युत्पन्न निरंतर होता है। वास्तव में, वक्र हर जगह अनंत,रूप से भिन्न होता है, जैसा कि होना चाहिए यदि यह वास्तव में एक वृत्त का प्रतिनिधित्व करता है। | ||
वक्र | वक्र पूर्णतया एक वृत्त का प्रतिनिधित्व करता है, लेकिन वृत्त की चाप लंबाई में बिल्कुल परमापीकरण नहीं है। उदाहरण के लिए इसका अर्थ है कि बिंदु <math>t</math> पर लाई नहीं है <math>(\sin(t), \cos(t))</math> प्रत्येक चतुर्थांश वृत्त के प्रारंभ, मध्य और अंत बिंदु को छोड़क शेष भाग सममितीय है। यह असंभव है, क्योंकि वृत्त का एक्स निर्देशांक एक सटीक तर्कसंगत बहुपद अभिव्यक्ति प्रदान करता है <math>\cos(t)</math>, जो असंभव है। वृत्त अपने मापदण्ड के रूप में एक पूर्ण क्रांति <math>t</math> 0 से <math>2\pi</math> तक जाता है, लेकिन यह केवल इसलिए है क्योंकि समूह सदिश को यादृच्छिक ढंग से <math>\pi/2</math>. गुणकों के रूप में चुना गया था | ||
== यह भी देखें == | == यह भी देखें == | ||
* | * स्पलाइन(गणित) | ||
* बेजियर सतह | * बेजियर सतह | ||
* डी बूर का | * डी बूर का कलन विधि | ||
* त्रिभुज | * त्रिभुज जाली | ||
* | * बिंदु का गुबारा | ||
* | * परिमय गति | ||
* | * आइसोज्यामितीय विश्लेषण | ||
== संदर्भ == | == संदर्भ == | ||
| Line 219: | Line 209: | ||
== बाहरी संबंध == | == बाहरी संबंध == | ||
* [http://www.rw-designer.com/NURBS Clear explanation of | * [http://www.rw-designer.com/NURBS Clear explanation of एनयूआरबीएस for non-experts] | ||
* [http://www.cs.wpi.edu/~matt/courses/cs563/talks/nurbs.html About Nonuniform Rational B-Splines – | * [http://www.cs.wpi.edu/~matt/courses/cs563/talks/nurbs.html About Nonuniform Rational B-Splines – एनयूआरबीएस] | ||
* [https://github.com/msteinbeck/tinyspline TinySpline: Opensource C-library with bindings for various languages] | * [https://github.com/msteinbeck/tinyspline TinySpline: Opensource C-library with bindings for various languages] | ||
| Line 228: | Line 218: | ||
[[Category:Articles with short description]] | [[Category:Articles with short description]] | ||
[[Category:Articles with unsourced statements from January 2021]] | [[Category:Articles with unsourced statements from January 2021]] | ||
[[Category:CS1 français-language sources (fr)]] | |||
[[Category:CS1 maint]] | |||
[[Category:CS1 Ελληνικά-language sources (el)]] | |||
[[Category:Citation Style 1 templates|W]] | |||
[[Category:Collapse templates]] | |||
[[Category:Created On 25/11/2022]] | [[Category:Created On 25/11/2022]] | ||
[[Category:Machine Translated Page]] | [[Category:Machine Translated Page]] | ||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with broken file links]] | [[Category:Pages with broken file links]] | ||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | [[Category:Short description with empty Wikidata description]] | ||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates based on the Citation/CS1 Lua module]] | |||
[[Category:Templates generating COinS|Cite web]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates used by AutoWikiBrowser|Cite web]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikipedia fully protected templates|Cite web]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:कंप्यूटर एडेड डिजाइन]] | [[Category:कंप्यूटर एडेड डिजाइन]] | ||
Latest revision as of 14:02, 9 December 2022
एनयूआरबीएस(नॉन-यूनिफार्म रैशनल बेसिस स्पलाइन) एक गणितीय मॉडल है। जो आधार विभाजन(बेसिस स्पलाइन) का उपयोग करता है। जो कंप्यूटर ग्राफिक्स वक्र में और इसके सतहों के प्रतिनिधित्व के लिए उपयोग किया जाता है। यह विश्लेषणात्मक(गणितीय सूत्रों द्वारा परिभाषित) और प्रतिरूपित आकृतियों को संभालने के लिए बहुत लचीलापन और सटीकता प्रदान करता है। यह एक प्रकार का वक्र प्रतिरूपण है, जो बहुभुज प्रतिरूपण या डिजिटल वास्तुशिल्प के विपरीत है। एनयूआरबीएस वक्र सामान्यतः कंप्यूटर एडेड डिजाइन(सीएडी), निर्माण(सीएएम) और अभियान्त्रिकी(सीएइ) में उपयोग किए जाते हैं। वे कई उद्योग-व्यापी मानकों का हिस्सा हैं, जैसे आईजीईएस, एसटीईपी, एसीआईएस और पीएचआईजीएस। एनयूआरबीएस सतहों को बनाने और संपादित करने के उपकरण विभिन्न 3D ग्राफिक्स और एनीमेशन सॉफ़्टवेयर पैकेजों में पाए जाते हैं।
ये कंप्यूटर क्रमादेश द्वारा कुशलता से देखे जा सकते हैं और आसानी से मानवीय संपर्क की अनुमति देते हैं। एनयूआरबीएस सतहें त्रि-आयामी क्षेत्र में एक सतह के लिए मानचित्रण दो मापदंडों के कार्य हैं। सतह का आकार नियंत्रण बिंदुओं द्वारा निर्धारित किया जाता है। एक सघन रूप में, एनयूआरबीएस सतहें सरल ज्यामितीय आकारों का प्रतिनिधित्व कर सकती हैं। जटिल जैविक आकृतियां के लिए टी- स्पलाइन और उपखंड सतहें अधिक उपयुक्त होती हैं क्योंकि वे एनयूआरबीएस की सतहों की तुलना में नियंत्रण बिंदुओं की संख्या को आधा कर देते हैं।
सामान्य रूप से, NURBS वक्रों और सतहों का संपादन सहज और पूर्वानुमेय है।[citation needed]नियंत्रण बिंदु सदैव या तो सीधे वक्र या सतह से जुड़े होते हैं, या फिर रबर बैंड की तरह काम करते हैं। उपयोगकर्ता अंतरापृष्ठ के आधार पर, एनयूआरबीएस घटता और सतहों का संपादन उनके नियंत्रण बिंदुओं (बेज़ियर वक्र के समान) या उच्च स्तरीय उपकरण जैसे स्पलाइन प्रतिरुपण और श्रेणीबद्ध संपादन के माध्यम से हो सकता है। उपयोगकर्ता अंतरापृष्ठ के आधार पर एनयूआरबीएस वक्र और सतह के संपादन को उनके नियंत्रण बिन्दुओं (बेयर वक्र के सदृश) या उच्च स्तरीय उपकरणों के जरिए किया जा सकता है जैसे स्पलाइन प्रतिरुपण और श्रेणीबद्ध संपादन के माध्यम से हो सकता है।
ऐतिहासिक पृष्ठभूमि
कंप्यूटर से पहले, विभिन्न प्रारूपण उपकरणों के साथ डिजाइनों को हाथ से कागज पर तैयार किया जाता था। सीधी रेखाओं के लिए पटरी, वृत्तों के लिए दिशा निरूपण यंत्र(आलेखन) और कोणों के लिए चांदा का उपयोग किया जाता था। लेकिन कई आकृतियाँ, जैसे किसी जहाज के स्वतंत्र वक्र, इन उपकरणों से नहीं बनाया जा सकता था। चूँकि इस तरह के वक्र को आलेखन बोर्ड में मुक़्त रूप से खींचा जा सकता है, जहाज़ बनाने वालों को अधिकांशता एक यथार्थ आकार संस्करण की आवश्यकता होती थी जो हाथ से नहीं किया जा सकता था। इस तरह के बड़े चित्र लकड़ी की लचीली स्पलाइन की मदद से बनाए जाते थे, स्पलाइन को कई पूर्व निर्धारित बिंदुओं पर रखा गया था, जिन्हें डक्स कहा जाता था डक्स के बीच, स्पलाइन सामग्री की लोच ने स्पलाइन को आकार लेने का कारण बना दिया जिससे बंकन की ऊर्जा कम हो गई, और इस प्रकार बाधाओं के अनुरूप असुविधाजनक संभव आकार का निर्माण किया। डक्स को खिसका कर आकार को समायोजित किया जा सकता है।[1]
1946 में, गणितज्ञों ने स्पलाइन आकार का अध्ययन करना शुरू किया, और भाषा के अनुसमूह बहुपद सूत्र का प्रवेशन किया, जिसे स्पलाइन(गणित) या स्पलाइन फलन के रूप में जाना जाता है। आई.जे.स्कोनबर्ग ने ड्राफ्ट्समैन द्वारा उपयोग किए जाने वाले यांत्रिक स्पलाइन के समानता के बाद स्पलाइन फलन को अपना नाम दिया।[2]
चूंकि कंप्यूटर को डिजाइन की प्रक्रिया में सम्मिलित किया गया, ऐसे स्पलाइन के भौतिक गुणों की जांच की गई ताकि उन्हें गणितीय सटीकता के साथ प्रतिरूपित किया जा सके और जहां आवश्यक हो, पुन: प्रस्तुत किया जा सके। रेनॉल्ट अभियान्ता, पियरे बेज़ियर और सिट्रोएन के भौतिक विज्ञानी और गणितज्ञ पॉल डी कैस्टेलजौ द्वारा फ्रांस में अग्रणी कार्य किया था। उन्होंने लगभग एक दूसरे के समानांतर काम किया, लेकिन क्योंकि बेज़ियर ने अपने काम के परिणाम प्रकाशित किए, बेज़ियर वक्र का नाम उनके नाम पर रखा गया, जबकि डी कैस्टेलजौ का नाम संबंधित कलन विधि से जुड़ा है।
पहले एनयूआरबीएस का उपयोग केवल कार कंपनियों के मालिकाना(सीएडी) पैकेज में किया जाता था। बाद में वे मानक कंप्यूटर ग्राफिक्स पैकेज का हिस्सा बन गए।
रीयल-टाइम, एनयूआरबीएस वक्र और सतहों का पारस्परिक प्रतिपादन पहली बार 1989 में सिलिकॉन ग्राफिक्स कार्यस्थल पर व्यावसायिक रूप से उपलब्ध कराया गया था। 1993 में, पीसीएस के लिए पहला पारस्परिक एनयूआरबीएस मॉडेलर, जिसे नोआरबीएस कहा जाता है, बर्लिन के तकनीकी विश्वविद्यालय के साथ सहयोग करने वाली एक छोटी सी कंपनी सीएएस बर्लिन द्वारा विकसित किया गया था।
निरंतरता
निर्माणाधीन एक सतह, के उदाहरण में एक मोटर याट का पतवार सामान्यतः कई एनयूआरबीएस सतहों से बना होता है जिन्हें एनयूआरबीएस पैच(या सिर्फ पैच) के रूप में जाना जाता है। इन सतह पैचों को इस तरह से एक साथ फिट किया जाता है कि सीमाएं अदृश्य हों। यह गणितीय रूप से ज्यामितीय परमापीय की अवधारणा द्वारा व्यक्त किया जाता है।
उच्च-स्तरीय उपकरण उपलब्ध हैं जो विभिन्न स्तरों की ज्यामितीय परमापीय बनाने और स्थापित करने के लिए एनयूआरबीएस की क्षमता से लाभान्वित होते हैं।
- स्थितीय परमापीय(G0) संचालित करता है जब दो वक्रों या सतहों की अंतिम स्थिति संपाती होती है। वक्र या सतहें अभी भी एक कोण पर मिल सकते हैं, जो एक तेज कोने या किनारे को जन्म देती हैं और टूटी हुई झलकियाँ का कारण बनती हैं।
- स्पर्शरेखा परमापीय(G¹) के लिए आवश्यक है कि वक्र या सतहों के अंत सदिश समानान्तर होते है और एक ही दिशा में, तेज किनारों को अस्वीकृत करते हैं। क्योंकि स्पर्शरेखीय रूप से निरंतर किनारे पर पड़ने वाले झलकियाँ सदैव निरंतर होती हैं और स्वाभाविक प्रतीत होता है कि परमापीय का यह स्तर प्रायः पर्याप्त हो सकता है।
- वक्रता परमापीय(G²) के लिए अंत सदिशों की समान लंबाई और लंबाई परिवर्तन की दर की आवश्यकता होती है। वक्रता-निरंतर किनारे पर गिरने वाली झलकियाँ कोई भी परिवर्तन प्रदर्शित नहीं करती हैं, जिससे दो सतहें एक जैसी दिखाई देती हैं। यह देखने में पूर्णतया समतल है। परमापीय का यह स्तर उन मॉडलों के निर्माण में बहुत उपयोगी है जिनके लिए एक निरंतर सतह बनाने के लिए कई द्वि-घन पैच की आवश्यकता होती है।
ज्यामितीय परमापीय मुख्य रूप से परिणामी सतह के आकार को संदर्भित करती है; चूँकि एनयूआरबीएस सतहें फलन करती हैं, और मापदंडों के संबंध में सतह के व्युत्पन्न पर वाद-विवाद करना संभव होता है। इसे प्राचलिक परमापीय के रूप में जाना जाता है। और किसी दिए गए मात्रा की प्राचलिक परमापीय का तात्पर्य उस मात्रा की ज्यामितीय परमापीय से होती है
प्रथम- और द्वितीय-स्तर प्राचलिक परमापीय(C0 और C¹) स्थितीय और स्पर्शरेखा(G0 और G¹) परमापीय के समान व्यावहारिक उद्देश्यों के लिए हैं। तृतीय-स्तरीय प्राचलिक परमापीय(C²), चूँकि, वक्रता परमापीय से अलग है क्योंकि इसका परमापीकरण भी निरंतर होता है। व्यवहार में, यदि समान बी- स्पलाइन का उपयोग किया जाता है तो C² का परमापीय प्राप्त करना आसान होता है।
Cn परमापीय की परिभाषा के लिए आवश्यक है कि सन्निकट वक्रों/सतहों का nवां व्युत्पन्न() जोड़ पर बराबर होते हैं।[3] ध्यान दें कि वक्रों और सतहों के(आंशिक) व्युत्पन्न सदिश होते हैं जिनकी दिशा और परिमाण दोनों बराबर होते है।
झलकियाँ और प्रतिबिंब उत्तम सपाटकरण को प्रकट करते हैं, जो कि एनयूआरबीएस सतहों के बिना प्राप्त करना व्यावहारिक रूप से असंभव है, जिसमें कम से कम G² परमापीय होता है। इस सिद्धांत का उपयोग सतह मूल्यांकन विधियों में से एक के रूप में किया जाता है जिससे किसी सतह की एक किरण का पता लगाया जाता है या उस पर प्रतिबिंबित होने वाली सफेद धारियों वाली छवि किसी सतह या सतहों के समुच्चय पर सबसे छोटे विचलन को भी दिखाती है। यह विधि कार प्रतिमान से ली गई है, जिसमें कार की सतह पर नियॉन-लाइट छत के प्रतिबिंबों की गुणवत्ता की जांच करके सतह की गुणवत्ता का निरीक्षण किया जाता है। इस पद्धति को ज़ेबरा विश्लेषण के रूप में जाना जाता है।
तकनीकी विनिर्देश
एक एनयूआरबीएस वक्र को उसके क्रम, भारित नियंत्रण बिंदुओं के एक समुच्चय और एक समूह सदिश द्वारा परिभाषित किया गया है।[4] एनयूआरबीएस वक्र और सतहें बी- स्पलाइन और बेज़ियर वक्रों और सतहों दोनों का सामान्यीकरण हैं, प्राथमिक अंतर नियंत्रण बिंदुओं का भार है, जो एनयूआरबीएस वक्रो को तर्कसंगत बनाता है। गैर- परिमय, अन्य सरल, बी- स्पलाइन का एक विशेष स्थिति का सब समुच्चय है, जहां प्रत्येक नियंत्रण बिंदु एक समांगी निर्देशांक के अतिरिक्त एक नियमित गैर-समरूप समन्वय 'डब्ल्यू' है।[5] यह प्रत्येक नियंत्रण बिंदु पर वजन 1 होने के बराबर है, पर्याप्त बी- स्पलाइन प्रत्येक नियंत्रण बिंदु के 'w' भार के रूप में उपयोग करते हैं।[6])
नियंत्रण बिंदुओं के दो विमीय जाल का उपयोग करके, समतल पैच और गोले के वर्गों सहित एनयूआरबीएस सतहों को बनाया जा सकता है। इन्हें सामान्यतः एस टी या यू वी नामक दो चर के साथ परमापीकरण किया जाता है। इसे एनयूआरबीएस प्रतिचित्रण बनाने के लिए यादृच्छिक विमा तक बढ़ाया जा सकता है।
एनयूआरबीएस वक्र और सतहें कई कारणों से उपयोगी हैं।
- किसी दिए गए क्रम के लिए एनयूआरबीएस का समुच्चय सजातीय रूपांतरण के तहत अपरिवर्तनीय होता है।[7] घूर्णन और परिक्रमणहीन एक समान गतिविधि जैसे संचालनों को उनके नियंत्रण बिंदुओं पर लागू करके एनयूआरबीएस वक्रों और सतहों पर लागू किया जा सकता है।
- वे मानक विश्लेषणात्मक आकृतियों(जैसे, शांकव) और मुक्त-रूप आकृतियों दोनों के लिए एक सामान्य गणितीय रूप प्रदान करते हैं।
- वे विभिन्न प्रकार की आकृतियों को डिजाइन करने के लिए लचीलापन प्रदान करते हैं।
- वे आकृतियों को संग्रहीत करते समय स्मरण शक्ति की ज़रूरत,को कम करते हैं(सरल तरीकों की तुलना में)।
- संख्यात्मक रूप से स्थिर और सटीक कलन विधि द्वारा उनका यथोचित शीघ्रता से मूल्यांकन किया जाता है।
यहाँ, एनयूआरबीएस अधिकतर एक विमीय वक्र में होता है, इसे दो सतहों या अधिक विमा के लिए सामान्यीकृत किया जा सकता है।
क्रम
एनयूआरबीएस वक्र का क्रम पास के नियंत्रण बिंदुओं की संख्या को परिभाषित करता है जो वक्र पर किसी दिए गए बिंदु को प्रभावित करते हैं। वक्र को वक्र के क्रम से एक कोटि कम के बहुपद द्वारा गणितीय रूप से दर्शाया जाता है। इसलिए, दूसरे क्रम के वक्र को रैखिक वक्र कहा जाता है(जो रैखिक बहुपदों द्वारा दर्शाए जाते हैं), तीसरे क्रम के वक्र को द्विघात वक्र कहा जाता है, और चौथे क्रम के वक्र को घन वक्र कहा जाता है। नियंत्रण बिंदुओं की संख्या वक्र के क्रम से अधिक या उसके बराबर होनी चाहिए।
प्रयोग में, क्यूबिक वक्र सबसे अधिक उपयोग किए जाने वाले हैं। पांचवें और छठे क्रम के वक्र कभी-कभी उपयोगी होते हैं, विशेष रूप से निरंतर उच्च क्रम के व्युत्पन्न प्राप्त करने के लिए है, लेकिन उच्च क्रम के वक्रों का व्यावहारिक रूप से कभी उपयोग नहीं किया जाता है। क्योंकि वे आंतरिक संख्यात्मक समस्याओं का कारण बनते हैं और असमान रूप से बड़ी गणना समय की आवश्यकता होती है।
नियंत्रण बिंदु
नियंत्रण बिंदु वक्र के आकार को निर्धारित करते हैं।[8] सामान्यतः, वक्र के प्रत्येक बिंदु की गणना कई नियंत्रण बिंदुओं का भारित योग करके की जाती है। प्रत्येक बिंदु का वजन शासकीय मापदण्ड के अनुसमूह भिन्न होता है। कोटि डी के वक्र के लिए, मापदण्ड के क्षेत्र डी + 1 अंतराल में किसी भी नियंत्रण बिंदु का वजन केवल गैर-शून्य होता है। उन अंतरालों के भीतर, कोटि डी के बहुपद फलन(आधार फलन) के अनुसमूह वजन बदलता है। और अंतराल की सीमाओं पर, आधार फलन सुचारू रूप से बहुपद की कोटि द्वारा निर्धारित किया जाता है और समतलता शून्य करने के लिए जाना जाता है।
एक उदाहरण के रूप में, कोटि का आधार फलन त्रिकोण फलन होता है। यह शून्य से 1 तक बढ़ता है, फिर शून्य पर गिर जाता है। जब यह बढ़ता है, तो पिछले नियंत्रण बिंदु का आधार फलन गिरता है। इस प्रकार, वक्र दो बिंदुओं के बीच प्रक्षेपित होता है और परिणामी वक्र एक बहुभुज होता है, जो निरंतर, लेकिन अंतराल सीमाओं या समूह पर भिन्न नहीं होता है।.उच्च कोटि के बहुपदों में संगत रूप से अधिक अविच्छिन्न क्षेत्र होते हैं। ध्यान दें कि अंतराल के भीतर आधार फलन की बहुपद प्रकृति और निर्माण की रैखिकता वक्र को पूरी तरह समतल बनाती है, इसलिए केवल समूहों पर ही विच्छिन्नता उत्पन्न हो सकती है।
कई अनुप्रयोगों में तथ्य यह है कि एक एकल नियंत्रण बिंदु केवल उन अंतरालों को प्रभावित करता है जहां यह सक्रिय होता है, एक अत्यधिक वांछनीय गुण है, जिसे 'स्थानीय समर्थन' के रूप में जाना जाता है। प्रतिरूपण में, यह अन्य भागों को अपरिवर्तित रखते हुए सतह के एक हिस्से को बदलने की अनुमति देता है।
अधिक नियंत्रण बिंदुओं को जोड़ने से किसी दिए गए वक्र के लिए बेहतर सन्निकटन की अनुमति मिलती है, यद्यपि वक्रों का एक निश्चित वर्ग को नियंत्रण बिंदुओं की सीमित संख्या के साथ सटीक रूप से प्रदर्शित किया जा सकता है। एनयूआरबीएस वक्र में प्रत्येक नियंत्रण बिंदु के लिए एक अदिश भार होता है। यह नियंत्रण बिंदुओं की संख्या को अनावश्यक रूप से बढ़ाए बिना वक्र के आकार पर अधिक नियंत्रण की अनुमति देता है। विशेष रूप से, यह वक्रों के समुच्चय में वृत्तो और दीर्घवृत्त जैसे शंकु वर्गों को जोड़ता है जिन्हें सटीक रूप से प्रदर्शित किया जा सकता है। एनयूआरबीएस में तर्कसंगत शब्द इन भारों को को दर्शाता है।
नियंत्रण बिंदुओं में कोई भी विमीय हो सकता है। एक-विमीय बिंदु केवल मापदण्ड के अदिश(गणित) फलन को परिभाषित करते हैं। सामान्यतया इनका उपयोग प्रतिबिंब संसाधन फलन में चमक और रंग वक्रो को समायोजित करने के लिए किया जाता है। 3डी प्रतिरूपण में त्रि-विमीय नियंत्रण बिंदुओं का बहुलता से प्रयोग किए जाते हैं, जहाँ हर प्रकार के 3 डी क्षेत्र में "बिंदु" शब्द के प्रत्येक अर्थ में उनका प्रयोग किया जाता है। समय-चालित मूल्यों के समुच्चय को नियंत्रित करने के लिए बहु-विमीय बिंदुओं का उपयोग किया जा सकता है, उदाहरण के लिए एक रोबोट भुजा की विभिन्न स्थितीय और घूर्णी समुच्चय, एनयूआरबीएस सतहें का एक अनुप्रयोग हैं। प्रत्येक नियंत्रण 'बिंदु' वास्तव में वक्र को परिभाषित करते हुए नियंत्रण बिंदुओं का एक पूर्ण सदिश है। ये वक्र अपनी कोटि और नियंत्रण बिंदुओं की संख्या साझा करते हैं, और मापदंड के क्षेत्र एक विमीय को फैलाते हैं। मापदंड क्षेत्र के दूसरे विमीय पर इन नियंत्रण सदिश को प्रक्षेपित करके, वक्रों का एक सतत समुच्चय प्राप्त किया जाता है, जो सतह को परिभाषित करता है।
समूह सदिश
समूह सदिश, मापदंड मानों का एक अनुक्रम होता है, जो यह निर्धारित करता है कि नियंत्रण बिंदु कहां और कैसे एनयूआरबीएस वक्र को प्रभावित करते हैं। समूह की संख्या सदैव नियंत्रण बिंदुओं की संख्या प्लस वक्र की कोटि प्लस वन के बराबर होती है,(जैसे नियंत्रण बिंदुओं की संख्या और वक्र क्रम के बराबर होते है)। समूह सदिश पहले उल्लेखित अंतराल में प्राचलिक क्षेत्र को विभाजित करता है, जिसे सामान्यतया समूह अवधि के नाम से जाना जाता है। प्रत्येक बार मापदण्ड मान एक नए समूह विस्तार में प्रवेश करता है, एक नया नियंत्रण बिंदु सक्रिय हो जाता है, जबकि एक पुराने नियंत्रण बिंदु को त्याग दिया जाता है। यह निम्नानुसमूह है कि समूह सदिश में मान गैर-घटते क्रम में होना चाहिए, इसलिए(0, 0, 1, 2, 3, 3) मान्य है जबकि(0, 0, 2, 1, 3, 3) नहीं है।
क्रमिक समूह का समान मूल्य हो सकता है। यह तब शून्य लंबाई के समूह अवधि को परिभाषित करता है, जिसका अर्थ है कि दो नियंत्रण बिंदु एक ही समय में सक्रिय होते हैं(और निश्चित रूप से दो नियंत्रण बिंदु निष्क्रिय हो जाते हैं)। इसका परिणामी वक्र या इसके उच्च व्युत्पन्नों की परमापीय पर प्रभाव पड़ता है, उदाहरण के लिए, यह एक अन्य समतल एनयूआरबीएस वक्र में कोनों के निर्माण की अनुमति देता है। कई संयोगी समूह को कभी-कभी एक निश्चित 'बहुलता' वाली समूह के रूप में संदर्भित किया जाता है। दो या तीन की बहुलता वाली समूह को दोहरी या तिहरी समूह कहा जाता है। समूह की बहुलता वक्र की कोटि तक सीमित होती है, चूँकि एक उच्च बहुलता वक्र को अलग-अलग भागों में विभाजित कर देगी और यह नियंत्रण बिंदुओं को अप्रयुक्त छोड़ देगी। प्रथम-कोटि एनयूआरबीएस के लिए, प्रत्येक समूह को एक नियंत्रण बिंदु के साथ जोड़ा जाता है।
समूह सदिश सामान्यतः एक समूह से शुरू होता है जिसमें बहुलता क्रम के बराबर होती है। यह समझ में आता है, क्योंकि यह उन नियंत्रण बिंदुओं को सक्रिय करता है जिनका प्रभाव पहली समूह की अवधि पर पड़ता है। इसी तरह, समूह सदिश सामान्यतः उस बहुलता की समूह के साथ समाप्त होता है। ऐसे समूह सदिश वाले वक्र एक नियंत्रण बिंदु पर शुरू और समाप्त होते हैं।
समूह के मान निविष्टि मापदण्ड और संबंधित एनयूआरबीएस मान के बीच मानचित्रण को नियंत्रित करते हैं। उदाहरण के लिए, यदि एनयूआरबीएस क्षेत्र के माध्यम से किसी पथ का वर्णन करती है, तो समूह उस समय को नियंत्रित करती हैं जब फलन नियंत्रण बिंदुओं से आगे बढ़ता है। आकृतियों का प्रतिनिधित्व करने के प्रयोजनों के लिए, चूँकि, समूह मूल्यों के बीच के अंतर का अनुपात ही महत्व रखता है, उस स्थिति में, समूह सदिश(0, 0, 1, 2, 3, 3) और(0, 0, 2, 4, 6, 6) समान वक्र उत्पन्न करते हैं। समूह मूल्यों की स्थिति मापदण्ड क्षेत्रौ के मानचित्रण को वक्र क्षेत्र पर प्रभावित करती है। एक एनयूआरबीएस वक्र का प्रतिपादन सामान्यतः मापदण्ड रेंज के माध्यम से एक निश्चित कदम के साथ किया जाता है। समूह अवधि की लंबाई बदलकर, क्षेत्रों में प्रतिरूप बिंदुओं का उपयोग किया जा सकता है, जहां वक्रता अधिक होती है। एक अन्य उपयोग उन स्थितियों में होता है जहां मापदण्ड मान का कुछ भौतिक महत्व होता है, उदाहरण के लिए यदि मापदण्ड समय है और वक्र एक रोबोट भुजा की गति का वर्णन करता है। समूह की लंबाई फिर वेग और त्वरण में तब्दील हो जाती है, जो रोबोट के भुजा या उसके पर्यावरण को नुकसान से बचाने के लिए सही पाने के लिए आवश्यक हैं। मानचित्रण में यह लचीलापन है जो एनयूआरबीएस में गैर-समान वाक्यांश को संदर्भित करता है।
केवल आंतरिक गणना के लिए ही आवश्यक है, समूह सामान्यतः प्रतिरूपण सॉफ़्टवेयर के उपयोगकर्ताओं के लिए सहायक नहीं होते हैं। इसलिए, कई प्रतिरूपण अनुप्रयोग समूह को संपादन योग्य या यहां तक कि दृश्यमान नहीं बनाते हैं। नियंत्रण बिंदुओं में भिन्नता को देखकर सामान्यतः उचित समूह सदिश स्थापित करना संभव होता है। एनयूआरबीएस सॉफ़्टवेयर के नवीनतम संस्करण संस्करण(जैसे, ऑटोडेस्क माया और गैंडा 3D) समूह की स्थिति के पारस्परिक संपादन की अनुमति देते हैं, लेकिन यह नियंत्रण बिंदुओं के संपादन की तुलना में काफी कम सहज ज्ञान युक्त होते है।
आधार फलनों का निर्माण
एनयूआरबीएस वक्रों के निर्माण में उपयोग किए जाने वाले B- स्पलाइन आधार फलनों को सामान्यतः से चिह्नित किया जाता है, जिसमें के अनुरूप कार्य होता है, और वें नियंत्रण बिंदु, और आधार फलन की कोटि साथ मेल खाती है।[9] मापदण्ड निर्भरता को सदैव छोड़ दिया जाता है, इसलिए हम .लिख सकते हैं, इन आधार फलनों की परिभाषा में पुनरावर्ती है कोटि -0 फलन टुकड़े-टुकड़े में स्थिर फलन हैं। वे संबंधित समूह अवधि पर एक हैं और हर जगह शून्य हैं। प्रभावी रूप से, का एक रैखिक प्रक्षेप है तथा . बाद के दो फलन समूह विस्तार के लिए गैर-शून्य हैं, समूह विस्तार के लिए अतिव्यापन होते है। फलन की गणना
: के रूप में की जाती है
रैखिक रूप से अंतराल शून्य से एक तक बढ़ता है जहां गैर-शून्य है, जबकि अंतराल पर एक से शून्य तक गिर जाता है जहां गैर-शून्य है। जैसा पहले बताया गया है, एक त्रिकोणीय फलन है, पहले पर शून्य से एक तक बढ़ते हुए दो समूह विस्तार पर अशून्य, और दूसरी समूह अवधि पर शून्य तक गिरना। उच्च क्रम के आधार फलन गैर-शून्य होते हैं जो कि अधिक समूह फैलाव के अनुरूप होते हैं और इसके अनुरूप उच्च कोटि होती है। यदि मापदण्ड है, और के वें समूह है तथा इन्हे हम फलन f और g के रूप में लिख सकते हैं।
तथा
फलन तथा धनात्मक होते हैं जब संगत निचले क्रम के आधार फलन गैर-शून्य होते हैं। n पर गणितीय आगमन से यह पता चलता है कि के सभी मानों के लिए आधार फलन तथा गैर-ऋणात्मक होते है, यह आधार फलन की गणना को संख्यात्मक रूप से स्थिर बनाता है।
फिर से प्रेरण द्वारा, यह साबित किया जा सकता है कि मापदण्ड के किसी विशेष मान के लिए आधार फलनों का योग एकात्मकता होती है। इसे आधार फलनों के एकात्मकता गुण के विभाजन के रूप में जाना जाता है।
आंकड़े समूह के लिए रैखिक और द्विघात आधार फलनों को दिखाते हैं {..., 0, 1, 2, 3, 4, 4.1, 5.1, 6.1, 7.1, ...}
एक समूह विस्तार अन्य की तुलना में काफी कम होता है। उस समूह की अवधि पर, द्विघात आधार फलन में में शिखर अधिक विशिष्ट है, लगभग एक तक पहुँचने के विपरीत, निकटवर्ती आधार फलन अधिक तेज़ी से शून्य हो जाते हैं। ज्यामितीय व्याख्या में, इसका मतलब है कि वक्र संबंधित नियंत्रण बिंदु के करीब पहुंचता है। एक डबल समूह के स्थिति में, समूह अवधि की लंबाई शून्य हो जाती है और शिखर एक तक पहुँच जाता है। आधार फलन अब उस बिंदु पर भिन्न नहीं है। यदि निकटतम नियंत्रण बिंदु समरेख नहीं हैं तो वक्र पर नुकीला कोना होगा।
एक एनयूआरबीएस वक्र का सामान्य रूप
आधार फलनों की परिभाषाओं का उपयोग करना पिछले अनुच्छेद से, एक एनयूआरबीएस वक्र निम्न रूप लेता है[9]
इसमें, नियंत्रण बिंदुओं की संख्या है तथा संगत भार हैं। भाजक एक सामान्य कारक है जो एक का मूल्यांकन करता है यदि सभी भार एक हैं। और इसे आधार फलनों की एकात्मकता गुण के विभाजन के रूप में देखा जाता है। इसे इस रूप में लिखने की प्रथा है
जिसमें फलन को,
परिमेय आधार फलन के रूप में जाना जाता है।
एक एनयूआरबीएस सतह का सामान्य रूप
एक एनयूआरबीएस सतह को दो एनयूआरबीएस वक्रों के प्रदिश गुणनफल के रूप में प्राप्त किया जाता है, इस प्रकार दो स्वतंत्र मापदंडों का उपयोग किया जाता है तथा सूचकांक के साथ तथा क्रमश [9]
साथ
तर्कसंगत आधार फलनों के रूप में होता है।
एनयूआरबीएस वस्तुओं में हेरफेर करना
कई रूपांतरणों को एक एनयूआरबीएस वस्तु पर लागू किया जा सकता है। उदाहरण के लिए, यदि वक्र को एक निश्चित कोटि और N नियंत्रण बिंदुओं के उपयोग से परिभाषित किया जाता है, तो वक्र को कोटि और N+1 नियंत्रण बिंदुओं का उपयोग करते हुए व्यक्त किया जा सकता है। इस प्रक्रिया में कई नियंत्रण बिंदु स्थिति को बदलते हैं और समूह सदिश में एक समूह अन्तर्स्थापित की जाती है। पारस्परिक डिज़ाइन के दौरान इन परिचालन का बड़े पैमाने पर उपयोग किया जाता है। नियंत्रण बिंदु जोड़ते समय, वक्र का आकार वही रहना चाहिए, जिससे आगे के समायोजन के लिए शुरुआती बिंदु बन सके। इनमें से कई संक्रिया पर नीचे चर्चा की गई है।[9][10]
समूह सम्मिलन
जैसा कि शब्द से पता चलता है, समूह सम्मिलन समूह सदिश में एक समूह सम्मिलित करता है। यदि वक्र की कोटि है, तो नियंत्रण बिंदुओं को द्वारा प्रतिस्थापित किया जाता है और एक नए वक्र का आकार समान रहता है।
एक समूह की अधिकतम बहुलता, को कई बार अन्तर्निविष्ट किया जाता है। इसे कभी-कभी समूह शोधन के रूप में संदर्भित किया जाता है और इसे एक कलां विधि द्वारा प्राप्त किया जा सकता है जो बार-बार समूह सम्मिलन की तुलना में अधिक कुशल होते है।
समूह हटाना
समूह हटाना समूह सम्मिलन का उल्टा है। इसका उद्देश्य अधिक सघन प्रतिनिधित्व प्राप्त करने के लिए समूह और संबंधित नियंत्रण बिंदुओं को हटाना है। स्पष्ट है कि वक्र की सही आकृति को बनाए रखते हुए यह सदैव संभव नहीं होता है। व्यवहार में, सटीकता में सहिष्णुता का उपयोग यह निर्धारित करने के लिए किया जाता है कि क्या समूह को हटाया जा सकता है। प्रक्रिया का उपयोग एक पारस्परिक सत्र के बाद परिशोधन के लिए किया जाता है जिसमें नियंत्रण बिंदुओं को हस्तचालित रूप से या प्राप्त करने के बाद जोड़ा जा सकता है, जहां एक सीधी रूपांतरण प्रक्रिया निरर्थक नियंत्रण बिंदुओं की ओर ले जाती है
कोटि उन्नयन
किसी विशेष कोटि के एनयूआरबीएस वक्र को सदैव उच्च कोटि के एनयूआरबीएस वक्र द्वारा दर्शाया जाता है। अलग-अलग एनयूआरबीएस वक्र को जोड़ते समय इसका अधिकांशता उपयोग किया जाता है, उदाहरण के लिए, एनयूआरबीएस वक्र के एक समुच्चय के बीच एनयूआरबीएस सतह बनाते समय या आसन्न वक्र को एकीकृत करता है। प्रक्रिया में, विभिन्न वक्रों को एक ही कोटि तक लाया जाना चाहिए, अधिकांशता वक्रों के समुच्चय की अधिकतम कोटि होती है, इस प्रक्रिया को कोटि ऊंचाई के रूप में जाना जाता है।
वक्रता
विभेदक ज्यामिति में सबसे महत्वपूर्ण गुण वक्रता .है, यह स्थानीय गुण किनारों, कोनों आदि का वर्णन करता है। और पहली और दूसरी व्युत्पन्न के बीच संबंधों का वर्णन करता है, और इस प्रकार, सटीक वक्र आकार का वर्णन करता है। अवकलज निर्धारित करने के बाद गणना करना आसान है या दूसरे व्युत्पन्न से चाप की लम्बाई के रूप में अनुमानित .करता है। और वक्रता की सीधी गणना इन समीकरणों के साथ उनके बहुभुज अभ्यावेदन के विरुद्ध परिचालित वक्रों का बड़ा लाभ है।
उदाहरण: एक वृत्त

गैर-परिमय स्पलाइन या बेज़ियर वक्र एक वृत्त का अनुमान लगा सकते हैं, लेकिन वे इसका सटीक रूप से प्रतिनिधित्व नहीं कर सकते। परिमय स्पलाइन किसी भी शंकु खंड का प्रतिनिधित्व कर सकते हैं, जिनमें वृत्त भी सम्मिलित होते है, यह प्रतिनिधित्व अद्वितीय नहीं है, परंतु एक संभावना नीचे दिखाई देती है।
| x | y | z | भार |
|---|---|---|---|
| 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | |
| 0 | 1 | 0 | 1 |
| -1 | 1 | 0 | |
| -1 | 0 | 0 | 1 |
| -1 | -1 | 0 | |
| 0 | -1 | 0 | 1 |
| 1 | -1 | 0 | |
| 1 | 0 | 0 | 1 |
क्रम तीन है, क्योंकि एक वृत्त एक द्विघात वक्र है और स्पलाइन का क्रम इसके टुकड़े वार बहुपद खंडों की कोटि से एक अधिक है। समूह सदिश है वृत्त चार चौथाई वृत्तों से बना होता है जो दोहरे समूह के साथ बंधे होते हैं। चूँकि, तीसरे क्रम में डबल समूह एनयूआरबीएस वक्र सामान्य रूप से पहले अवकलज में निरंतरता के नुकसान का परिणाम होता है, नियंत्रण बिंदु इस तरह से स्थित हैं कि पहला व्युत्पन्न निरंतर होता है। वास्तव में, वक्र हर जगह अनंत,रूप से भिन्न होता है, जैसा कि होना चाहिए यदि यह वास्तव में एक वृत्त का प्रतिनिधित्व करता है।
वक्र पूर्णतया एक वृत्त का प्रतिनिधित्व करता है, लेकिन वृत्त की चाप लंबाई में बिल्कुल परमापीकरण नहीं है। उदाहरण के लिए इसका अर्थ है कि बिंदु पर लाई नहीं है प्रत्येक चतुर्थांश वृत्त के प्रारंभ, मध्य और अंत बिंदु को छोड़क शेष भाग सममितीय है। यह असंभव है, क्योंकि वृत्त का एक्स निर्देशांक एक सटीक तर्कसंगत बहुपद अभिव्यक्ति प्रदान करता है , जो असंभव है। वृत्त अपने मापदण्ड के रूप में एक पूर्ण क्रांति 0 से तक जाता है, लेकिन यह केवल इसलिए है क्योंकि समूह सदिश को यादृच्छिक ढंग से . गुणकों के रूप में चुना गया था
यह भी देखें
- स्पलाइन(गणित)
- बेजियर सतह
- डी बूर का कलन विधि
- त्रिभुज जाली
- बिंदु का गुबारा
- परिमय गति
- आइसोज्यामितीय विश्लेषण
संदर्भ
- ↑ Schneider, Philip. "एनयूआरबी कर्व्स: ए गाइड फॉर द अनिनिशिएटेड". MACTECH. Retrieved 26 September 2014.
- ↑ Schoenberg, I. J. (August 19, 1964). "तख़्ता कार्य और स्नातक की समस्या". Proceedings of the National Academy of Sciences of the United States of America. National Academy of Sciences. 52 (4): 947–950. doi:10.1073/pnas.52.4.947. PMC 300377. PMID 16591233.
- ↑ Foley, van Dam, Feiner & Hughes: Computer Graphics: Principles and Practice, section 11.2, Addison-Wesley 1996 (2nd ed.).
- ↑ बायो-इंस्पायर्ड सेल्फ-ऑर्गनाइजिंग रोबोटिक सिस्टम्स. p. 9. Retrieved 2014-01-06.
- ↑ "वाजिब बी-splines". www.cl.cam.ac.uk.
- ↑ "NURBS: परिभाषा". www.cs.mtu.edu.
- ↑ David F. Rogers: An Introduction to NURBS with Historical Perspective, section 7.1
- ↑ Gershenfeld, Neil (1999). गणितीय मॉडलिंग की प्रकृति. Cambridge University Press. p. 141. ISBN 0-521-57095-6.
- ↑ 9.0 9.1 9.2 9.3 Piegl, Les; Tiller, Wayne (1997). द एनयूआरबीएस बुक (2. ed.). Berlin: Springer. ISBN 3-540-61545-8.
- ↑ Piegl, L. (1989). "तर्कसंगत बी-स्प्लिन के आकार को संशोधित करना। भाग 1: घटता है". Computer-Aided Design. 21 (8): 509–518. doi:10.1016/0010-4485(89)90059-6.