एनवलप (गणित)

For दोलन संकेत का एनवलप, see एनवलप(तरंग). For सार अवधारणा, see एनवलप(श्रेणी सिद्धांत).

वक्र के एक समूह के एनवलप का निर्माण।

ज्यामिति में, वक्रों के समतलीय समूहों का एनवलप एक वक्र की भाँति होता है जो किसी बिंदु पर उसके समूहों के प्रत्येक सदस्य के लिए स्पर्शरेखा की भाँति प्रदर्शित होता हैं, और यह स्पर्शरेखा के बिंदु से मिलने पर एनवलप का निर्माण करता हैं। मौलिक रूप से, एनवलप पर कोई बिंदु दो विभिन्न प्रकार के आसन्न वक्रों के प्रतिच्छेदन के रूप में माना जाता हैं, जिसका अर्थ है इसके पास के वक्रों के प्रतिच्छेदन की सीमा(गणित) से होता है। यह विचार समतल में सतह(गणित) के किसी एनवलप के लिए सार्वभौमिक सामान्यीकरण से हो सकता है, और इसी के समान उच्च आयामों के लिए भी।

एनवलप के होने के लिए, यह जरूरी है कि इसके समूह के लिए परस्पर होने वाली यह घटना अलग-अलग सदस्यों के लिए अलग-अलग तरह से कई गुना हों क्योंकि स्पर्शरेखा की अवधारणा इसके कारण लागू नहीं होती है, और उपस्थित सदस्यों के माध्यम से इसके समतल की प्रवणता के प्रभाव पर प्रक्रिया होनी आवश्यक होती हैं। लेकिन ये शर्तें इस कारण पर्याप्त नहीं हैं - क्योंकि किसी दिए हुए समूह के पास एनवलप नहीं हो सकता है। इसका सरल उदाहरण विस्तारित त्रिज्या के संकेंद्रित वृत्तों के समूह द्वारा दिया गया है।

वक्र समूह का एनवलप

माना प्रत्येक वक्र C_t समूह में समीकरण f के समाधान के रूप में दिया जाना चाहिए f_t(x, y)=0(अंतर्निहित वक्र देखें), जहां t एक पैरामीटर है। F(t, x, y)=f लिखें _t(x, y) और मान लें कि F अवकलनीय है।

समूह का एनवलप C_t फिर समूह के रूप में परिभाषित किया गया है ${\mathcal {D}}$(x,y) के बिंदुओं जिसके लिए, एक साथ,

$F(t,x,y)=0~~{\mathsf {and}}~~{\partial F \over \partial t}(t,x,y)=0$

t के कुछ मूल्य के लिए,

जहाँ पर $\partial F/\partial t$ t के संबंध में F का आंशिक व्युत्पन्न है।

यदि t और u, t≠u पैरामीटर के दो मान हैं तो वक्र C_t के प्रतिच्छेदन और C_u द्वारा दिया गया है

$F(t,x,y)=F(u,x,y)=0\,$

या, समकक्ष,

$F(t,x,y)=0~~{\mathsf {and}}~~{\frac {F(u,x,y)-F(t,x,y)}{u-t}}=0.$

u → t करने से ऊपर की परिभाषा मिलती है।

एक महत्वपूर्ण विशेष स्थिति है जब F(t, x, y) t में बहुपद है। इसमें भाजक समाशोधन द्वारा, वह स्थिति सम्मलित किया गया है जहां F(t, x, y) t में तर्कसंगत फंक्शन है। इस स्थिति में, परिभाषित मात्रा t है जो F(t, x, y) का दोहरा मूल है, इसलिए एनवलप का समीकरण F के विविक्तकरण को 0 पर निहित करके पाया जा सकता है(क्योंकि परिभाषा कुछ समय पर F=0 की मांग करती है t और पहला व्युत्पन्न = 0 अर्ताथ इसका मान 0 है और यह उस t पर न्यूनतम/अधिकतम है)।

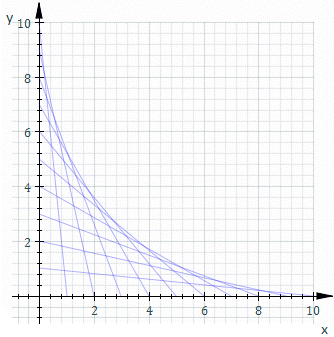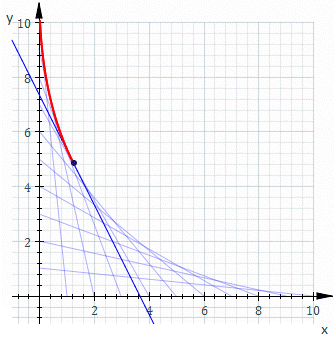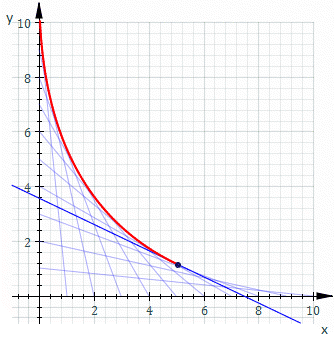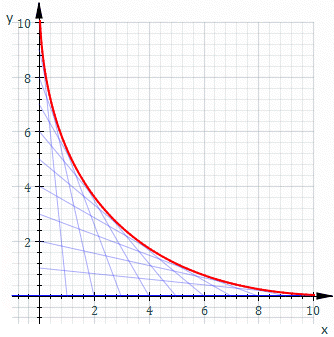
उदाहरण के लिए, C_t वह रेखा हो जिसका x और y प्रतिच्छेदन t और 11−t हैं, यह ऊपर के चित्रण में दिखाया गया है। C_t का समीकरण है

${\frac {x}{t}}+{\frac {y}{11-t}}=1$

या, भिन्न समाशोधन,

$x(11-t)+yt-t(11-t)=t^{2}+(-x+y-11)t+11x=0.\,$

एनवलप का समीकरण कुछ इस प्रकार है

$(-x+y-11)^{2}-44x=(x-y)^{2}-22(x+y)+121=0.\,$

अधिकांशतः जब F पैरामीटर का तर्कसंगत फंक्शन नहीं होता है तो इसे उचित प्रतिस्थापन द्वारा इस स्थिति में कम किया जा सकता है। उदाहरण के लिए, यदि समूह C_θ द्वारा दिया गया है फॉर्म के समीकरण के साथ u(x, y)cos θ+v(x, y)sin θ=w(x, y), फिर t=e^iθ रखने पर, cos θ=(t+1/t)/2, sin θ=(t-1/t)/2i वक्र के समीकरण को बदलता है

$u{1 \over 2}(t+{1 \over t})+v{1 \over 2i}(t-{1 \over t})=w$

या

$(u-iv)t^{2}-2wt+(u+iv)=0.\,$

एनवलप का समीकरण तब विवेचक को 0 पर समूह करके दिया जाता है:

$(u-iv)(u+iv)-w^{2}=0\,$

या

$u^{2}+v^{2}=w^{2}.\,$

वैकल्पिक परिभाषाएं

1. एनवलप E₁ पास के C_t के प्रतिच्छेदन की सीमा है।.
2. एनवलप E₂ C_t के सभी के लिए वक्र स्पर्शरेखा है।
3. एनवलप E₃ वक्र C_t द्वारा भरे गए क्षेत्र की सीमा है।

फिर $E_{1}\subseteq {\mathcal {D}}$, $E_{2}\subseteq {\mathcal {D}}$ तथा $E_{3}\subseteq {\mathcal {D}}$, जहाँ पर ${\mathcal {D}}$ इस उपखंड के मूल खंड की शुरुआत में परिभाषित बिंदुओं का समूह है।

उदाहरण

उदाहरण 1

ये परिभाषाएं E₁, तथा E₂, और E₃ एनवलप के अलग-अलग समूह हो सकते हैं। उदाहरण के लिए वक्र पर विचार करें y = x₃ द्वारा पैरामीट्रिज्ड γ : R → R₂ जहाँ पर γ(t) =(t,t₃). वक्रों का एक-पैरामीटर समूह स्पर्शरेखा रेखाओं द्वारा γ को दिया जाएगा।

पहले हम विवेचक ${\mathcal {D}}$ की गणना करते हैं जहाँ उत्पादक फलन है

$F(t,(x,y))=3t^{2}x-y-2t^{3}.$

आंशिक व्युत्पन्न की गणना F_t = 6t(x – t). यह या तो इस प्रकार है x = t या t = 0. पहले मान लीजिए x = t and t ≠ 0. f में प्रतिस्थापन: $F(t,(t,y))=t^{3}-y\,$

और इसलिए, यह मानते हुए कि t ≠ 0, यह इस प्रकार है F = F_t = 0 यदि और केवल यदि (x,y) = (t,t³). अगला, यह मानते हुए t = 0 और F में प्रतिस्थापित करना देता है F(0,(x,y)) = −y. तो मान रहे हैं t = 0, यह इस प्रकार है कि F = F_t = 0 यदि और केवल यदि y = 0. इस प्रकार विविक्तकर γ(0) पर मूल वक्र और इसकी स्पर्श रेखा है:

${\mathcal {D}}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\cup \{(x,y)\in \mathbb {R} ^{2}:y=0\}\ .$

आगे हम E₁ की गणना करते हैं, जहाँ इसे वक्र F(t,(x,y)) = 0 द्वारा दिया गया है और एक निकटवर्ती वक्र F(t + ε,(x,y)) द्वारा दिया गया है जहाँ ε कोई बहुत छोटी संख्या है। प्रतिच्छेदन बिंदु की सीमा को देखने से आता है F(t,(x,y)) = F(t + ε,(x,y)) क्योंकि ε शून्य हो जाता है। नोटिस जो F(t,(x,y)) = F(t + ε,(x,y)) यदि और केवल यदि

$L:=F(t,(x,y))-F(t+\varepsilon ,(x,y))=2\varepsilon ^{3}+6\varepsilon t^{2}+6\varepsilon ^{2}t-(3\varepsilon ^{2}+6\varepsilon t)x=0.$

यदि t ≠ 0 तब L के पास ε का केवल एक कारक है। ऐसा मानते हुए t ≠ 0 तो प्रतिच्छेदन द्वारा दिया गया है

$\lim _{\varepsilon \to 0}{\frac {1}{\varepsilon }}L=6t(t-x)\ .$

तब t ≠ 0 यह इस प्रकार है कि x = t. Y मान की गणना यह जानकर की जाती है कि यह बिंदु मूल वक्र γ की स्पर्श रेखा पर स्थित होना चाहिए: वह F(t,(x,y)) = 0. प्रतिस्थापित करने और हल करने से y = t^{3 प्राप्त होता है कब t = 0, L ε2 से विभाज्य है। ऐसा मानते हुए t = 0 तो प्रतिच्छेदन द्वारा दिया गया है}

$\lim _{\varepsilon \to 0}{\frac {1}{\varepsilon ^{2}}}L=3x\ .$

यह इस प्रकार है कि x = 0, और यह जानकर F(t,(x,y)) = 0 देता है y = 0. यह इस प्रकार है कि

$E_{1}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\ .$

आगे हम E₂ की गणना करते हैं, यह वक्र ही वह वक्र है जो अपनी स्वयं की सभी स्पर्श रेखाओं को स्पर्श करता है। यह इस प्रकार है कि

$E_{2}=\{(x,y)\in \mathbb {R} ^{2}:y=x^{3}\}\ .$

अंत में हम E₃की गणना करते हैं, समतल के प्रत्येक बिंदु में कम से कम एक स्पर्श रेखा होती है जो γ से होकर गुजरती है, और इसलिए स्पर्श रेखाओं द्वारा भरा गया क्षेत्र संपूर्ण तल है। सीमा E₃ इसलिए रिक्त समुच्चय है। सामान्यतः, समतल में दिए गए बिंदु पर विचार करें, जहाँ(x₀, y₀) वह बिंदु है जिस पर स्पर्शरेखा रेखा स्थित है लेकिन केवल तब जब ऐसा कोई t सम्मलित हों

$F(t,(x_{0},y_{0}))=3t^{2}x_{0}-y_{0}-2t^{3}=0\ .$

यह t में एक घन है और इस तरह कम से कम एक वास्तविक समाधान है। यह इस प्रकार है कि कम से कम एक स्पर्श रेखा γ को समतल में किसी दिए गए बिंदु से गुजरना चाहिए। यदि y > x³ तथा y > 0 तब प्रत्येक बिंदु(x, y) में γ से होकर गुजरने वाली बिल्कुल एक स्पर्श रेखा होती है। वही सच है यदि y < x³ y < 0. यदि y < x³ तथा y > 0 तब प्रत्येक बिंदु(x, y) में γ से होकर गुजरने वाली तीन अलग-अलग स्पर्श रेखाएँ होती हैं। वही सच है यदि y > x³ तथा y < 0. यदि y = x³ तथा y ≠ 0 तो प्रत्येक बिंदु(x, y) में इसके माध्यम से गुजरने वाली γ के लिए बिल्कुल दो स्पर्श रेखाएं होती हैं(यह क्यूबिक से मेल खाती है जिसमें एक साधारण रूट और एक दोहराया रूट होता है)। वही सच है यदि y ≠ x³ तथा y = 0. यदि y = x³ तथा x = 0, अर्थात।, x = y = 0, तो इस बिंदु के पास γ से गुजरने वाली एक एकल स्पर्श रेखा है(यह क्यूबिक से मेल खाती है जिसमें बहुलता 3 की एक वास्तविक जड़ है)। यह इस प्रकार है कि

$E_{3}=\varnothing .$

उदाहरण 2

यह प्लॉट बिंदुओं(t,0),(0,k - t) को जोड़ने वाली रेखाओं के समूह का एनवलप देता है, जिसमें k का मान 1 होता है।

स्ट्रिंग कला में समान दूरी वाले पिनों की दो पंक्तियों को क्रॉस-कनेक्ट करना साधारण बात है। क्या वक्र बनता है?

सरलता के लिए, पिनों को x- और y-अक्षों पर समूह करें; एक गैर-ऑर्थोगोनल लेआउट एक समन्वय रोटेशन और स्केलिंग(ज्यामिति) दूर है। एक सामान्य स्ट्रेट-लाइन थ्रेड दो बिंदुओं(0, k−t) और(t, 0) को जोड़ता है, जहाँ k स्वयं स्केलिंग स्थिरांक है, और लाइनों का समूह पैरामीटर t को अलग करके उत्पन्न होता है। साधारण ज्यामिति से, इस सरल रेखा का समीकरण y = −(k − t)x/t + k− t है। F(x,y,t) = 0 के रूप में पुनर्व्यवस्थित और कास्टिंग करना देता है:

$F(x,y,t)=-{\frac {kx}{t}}-t+x+k-y=0\,$

(1)

अब t के संबंध में f(एक्स, वाई, t) को अलग करें और परिणाम प्राप्त करने के लिए शून्य के बराबर परिणाम समूह करें

${\frac {\partial F(x,y,t)}{\partial t}}={\frac {kx}{t^{2}}}-1=0\,$

(2)

ये दोनों समीकरण संयुक्त रूप से एनवलप के समीकरण को परिभाषित करते हैं।(2) से हमारे पास है:

$t={\sqrt {kx}}\,$

t के इस मान को(1) में प्रतिस्थापित करना और सरल करना एनवलप के लिए एक समीकरण देता है:

$y=({\sqrt {x}}-{\sqrt {k}})^{2}\,$

(3)

या, और अधिक सुंदर रूप में पुनर्व्यवस्थित करना जो x और y के बीच समरूपता दिखाता है:

${\sqrt {x}}+{\sqrt {y}}={\sqrt {k}}$

(4)

हम अक्षों का एक चक्कर लगा सकते हैं जहां b अक्ष रेखा y=x उन्मुख उत्तर पूर्व है और a अक्ष रेखा y=−x दक्षिण पूर्व उन्मुख है। ये नए मूल x-y से संबंधित हैं x=(b+a)/√2 तथा y=(b−a)/√2, हम(4) में प्रतिस्थापन और विस्तार और सरलीकरण के बाद प्राप्त करते हैं,

$b={\frac {1}{k{\sqrt {2}}}}a^{2}+{\frac {k}{2{\sqrt {2}}}},$

(5)

जो स्पष्ट रूप से a=0, या y=x के साथ अक्ष के साथ एक पैराबोला के लिए समीकरण है।

उदाहरण 3

मान लीजिए I ⊂ 'R' एक खुला अंतराल है और γ : I → 'R'² चाप लंबाई द्वारा पैरामीट्रिज्ड एक चिकना समतल वक्र है। γ(I) के लिए सामान्य रेखाओं के एक-पैरामीटर समूह पर विचार करें। एक रेखा γ(t) पर γ के लिए सामान्य है यदि यह γ(t) से होकर गुजरती है और γ(t) पर γ के वक्र स्पर्शरेखा सदिश के विभेदक ज्यामिति के लंबवत है। चलो 't' इकाई स्पर्शरेखा वेक्टर को γ को दर्शाता है और 'n' वक्र सामान्य या वक्रता वेक्टर की इकाई विभेदक ज्यामिति को दर्शाता है। डॉट उत्पाद को निरूपित करने के लिए डॉट का उपयोग करके, सामान्य लाइनों के पैरामीटर समूह के लिए उत्पादक समूह दिया जाता है F : I × R² → R जहाँ पर

$F(t,{\mathbf {x} })=({\mathbf {x} }-\gamma (t))\cdot {\mathbf {T} }(t)\ .$

स्पष्ट रूप से(x − γ)·T = 0 यदि और केवल यदि x − γ T के लंबवत है, या समतुल्य है, यदि और केवल यदि x − γ N के समानांतर(ज्यामिति) है, या समकक्ष, यदि और केवल यदि x = γ कुछ λ ∈ R के लिए + λN। यह इस प्रकार है

$L_{t_{0}}:=\{{\mathbf {x} }\in \mathbb {R} ^{2}:F(t_{0},{\mathbf {x} })=0\}$

γ पर γ के लिए बिल्कुल सामान्य रेखा है(t₀). F का विविक्तकर ज्ञात करने के लिए हमें t के संबंध में इसके आंशिक अवकलज की गणना करनी होगी:

${\frac {\partial F}{\partial t}}(t,{\mathbf {x} })=\kappa (t)({\mathbf {x} }-\gamma (t))\cdot {\mathbf {N} }(t)-1\ ,$

जहाँ κ γ के समतल वक्रों की वक्रता है। यह देखा गया है कि F = 0 यदि और केवल यदि 'x' - γ = λ'N' कुछ λ ∈ 'R' के लिए। यह मानते हुए कि F = 0 देता है

${\frac {\partial F}{\partial t}}=\lambda \kappa (t)-1\ .$

यह मानते हुए कि κ ≠ 0 यह इस प्रकार है कि λ = 1/κ और इसी तरह

${\mathcal {D}}=\gamma (t)+{\frac {1}{\kappa (t)}}{\mathbf {N} }(t)\ .$

यह वक्र γ का ठीक-ठीक विकास है।

उदाहरण 4

बिंदुओं(s,0), ​​(0,t) को s से जोड़ने वाली रेखाओं के समूह के एनवलप के रूप में एक android^{2</सुप> + t2 = 1}

निम्नलिखित उदाहरण से पता चलता है कि कुछ स्थितियों में वक्रों के एक समूह के एनवलप को समुच्चयों के संघ की स्थलाकृतिक सीमा के रूप में देखा जा सकता है, जिसकी सीमाएँ एनवलप के वक्र हैं। के लिये $s>0$ तथा $t>0$ एक कार्तीय तल में(खुले) समकोण त्रिभुज पर विचार करें $(0,0)$, $(s,0)$ तथा $(0,t)$

$T_{s,t}:=\left\{(x,y)\in \mathbb {R} _{+}^{2}:\ {\frac {x}{s}}+{\frac {y}{t}}<1\right\}.$

घातांक $\alpha >0$ ठीक करें , और सभी त्रिभुजों के प्रतिच्छेदन $T_{s,t}$ पर विचार करें विवशतयः इसके अधीन $\textstyle s^{\alpha }+t^{\alpha }=1$, वह खुला समूह है

$\Delta _{\alpha }:=\bigcup _{s^{\alpha }+t^{\alpha }=1}T_{s,t}.$

के लिए कार्टेशियन $\textstyle \Delta _{\alpha }$ प्रतिनिधित्व लिखने के लिए, किसी से भी शुरू करें $\textstyle s>0$, $\textstyle t>0$ संतुष्टि देने वाला $\textstyle s^{\alpha }+t^{\alpha }=1$ और कोई भी $\textstyle (x,y)\in \mathbb {R} _{+}^{2}$. होल्डर असमानता#उल्लेखनीय विशेष मामले|होल्डर असमानता में $\textstyle \mathbb {R} ^{2}$ संयुग्मित घातांक के संबंध में $p:=1+{\frac {1}{\alpha }}$ तथा $\textstyle q:={1+\alpha }$ देता है:

$x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}\leq \left({\frac {x}{s}}+{\frac {y}{t}}\right)^{\frac {\alpha }{\alpha +1}}{\Big (}s^{\alpha }+t^{\alpha }{\Big )}^{\frac {1}{\alpha +1}}=\left({\frac {x}{s}}+{\frac {y}{t}}\right)^{\frac {\alpha }{\alpha +1}}$,

समानता के साथ यदि और केवल यदि $\textstyle s:\,t=x^{\frac {1}{1+\alpha }}:\,y^{\frac {1}{1+\alpha }}$. समूह के संघ के संदर्भ में बाद की असमानता पढ़ती है: बिंदु $(x,y)\in \mathbb {R} _{+}^{2}$ समूह के अंतर्गत आता है $\textstyle \Delta _{\alpha }$, अर्ताथ यह $\textstyle T_{s,t}$ का है साथ $\textstyle s^{\alpha }+t^{\alpha }=1$, यदि और केवल यदि यह संतुष्ट करता है

$x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}<1.$

इसके अलावा सीमा में $\mathbb {R} _{+}^{2}$ समूह का $\textstyle \Delta _{\alpha }$ रेखा खंडों के संबंधित समूह का एनवलप है

$\left\{(x,y)\in \mathbb {R} _{+}^{2}:\ {\frac {x}{s}}+{\frac {y}{t}}=1\right\}\ ,\qquad s^{\alpha }+t^{\alpha }=1$

(अर्थात त्रिभुजों के कर्ण), और कार्तीय समीकरण है

$x^{\frac {\alpha }{\alpha +1}}+y^{\frac {\alpha }{\alpha +1}}=1.$

ध्यान दें कि, विशेष रूप से, इसके मान $\alpha =1$ उदाहरण 2 के परवलय का चाप और $\alpha =2$ मान देता है(जिसका अर्थ है कि सभी कर्ण इकाई लंबाई खंड हैं) एस्ट्रॉइड देता है।

उदाहरण 5

प्रक्षेप्य की कक्षाओं का आवरण(निरंतर प्रारंभिक गति के साथ) एक अवतल परवलय है। प्रारंभिक गति 10 मीटर/सेकेंड है। हम g = 10 m/s लेते हैं^{2</उप>।}

हम गति में एनवलप के निम्नलिखित उदाहरण पर विचार करते हैं। मान लीजिए प्रारंभिक ऊंचाई 0 पर, एक प्रक्षेप्य के प्रक्षेपवक्र को निरंतर प्रारंभिक वेग v के साथ हवा में फेंकता है लेकिन अलग-अलग उन्नयन कोण θ। गतिमान सतह में x को क्षैतिज अक्ष होने दें, और y को ऊर्ध्वाधर अक्ष को निरूपित करने दें। फिर गति निम्नलिखित अंतर गतिशील प्रणाली देती है:

${\frac {d^{2}y}{dt^{2}}}=-g,\;{\frac {d^{2}x}{dt^{2}}}=0,$

जो चार प्रारंभिक शर्तों को पूरा करता है:

${\frac {dx}{dt}}{\bigg |}_{t=0}=v\cos \theta ,\;{\frac {dy}{dt}}{\bigg |}_{t=0}=v\sin \theta ,\;x{\bigg |}_{t=0}=y{\bigg |}_{t=0}=0.$

यहाँ t गति के समय को दर्शाता है, θ उन्नयन कोण है, g गुरुत्वाकर्षण त्वरण को दर्शाता है, और v निरंतर प्रारंभिक गति(वेग नहीं) है। उपरोक्त प्रणाली का समाधान एक अंतर्निहित फंक्शन कर सकता है:

$F(x,y,\theta )=x\tan \theta -{\frac {gx^{2}}{2v^{2}\cos ^{2}\theta }}-y=0.$

इसके एनवलप समीकरण को खोजने के लिए, कोई वांछित व्युत्पन्न की गणना कर सकता है:

${\frac {\partial F}{\partial \theta }}={\frac {x}{\cos ^{2}\theta }}-{\frac {gx^{2}\tan \theta }{v^{2}\cos ^{2}\theta }}=0.$

θ को हटाकर, निम्नलिखित एनवलप समीकरण तक पहुंच सकता है:

$y={\frac {v^{2}}{2g}}-{\frac {g}{2v^{2}}}x^{2}.$

स्पष्ट रूप से परिणामी एनवलप भी अवतल फलन परवलय है।

सतहों के एक समूह का एनवलप

त्रि-आयामी यूक्लिडियन अंतरिक्ष में सतहों का एक-पैरामीटर समूह समीकरणों के एक समूह द्वारा दिया जाता है

$F(x,y,z,a)=0$

एक वास्तविक पैरामीटर ए पर निर्भर करता है। उदाहरण के लिए, सतह में एक वक्र के साथ सतह पर स्पर्शरेखा समतल ऐसे समूह का निर्माण करते हैं।

अलग-अलग मानों a और a' से संबंधित दो सतहें द्वारा परिभाषित एक सामान्य वक्र में प्रतिच्छेद करती हैं

$F(x,y,z,a)=0,\,\,{F(x,y,z,a^{\prime })-F(x,y,z,a) \over a^{\prime }-a}=0.$

सीमा में जैसे a' a की ओर अग्रसर होता है, यह वक्र सतह में समाहित वक्र की ओर झुक जाता है

$F(x,y,z,a)=0,\,\,{\partial F \over \partial a}(x,y,z,a)=0.$

इस वक्र को 'a' पर समूह की विशेषता कहा जाता है। जैसा कि a भिन्न होता है, इन चित्रित वक्रों का स्थान एक सतह को परिभाषित करता है जिसे सतहों के समूह का एनवलप कहा जाता है।

सतहों के समूह के एनवलप के उस सतह में विशेष वक्र के साथ समूह में प्रत्येक सतह पर स्पर्शरेखा है।

सामान्यीकरण

चिकने सबमनिफोल्ड्स के इस समूह के एनवलप का विचार स्वाभाविक रूप से अनुसरण करता है। सामान्यतः यदि हमारे पास कोडिमेंशन C के साथ सबमैनिफोल्ड्स का समूह है तो हमें कम से कम ऐसे सबमैनीफोल्ड्स का C-पैरामीटर समूह होना चाहिए। उदाहरण के लिए: त्रि समतल(c = 2) में वक्रों का एक-पैरामीटर समूह, सामान्य रूप से, एनवलप नहीं होता है।

अनुप्रयोग

साधारण अंतर समीकरण

एनवलप सामान्य अंतर समीकरणों(ode) के अध्ययन से जुड़े हुए हैं, और विशेष रूप से ओडीई के एकवचन समाधान। उदाहरण के लिए, परवलय y = x^{2 की स्पर्श रेखाओं के एक-पैरामीटर समूह पर विचार करें ये उत्पादक समूह द्वारा दिए जाते हैं F(t,(x,y)) = t2 – 2tx + y. शून्य स्तर समूह F(t₀,(x,y)) = 0 बिंदु पर पैराबोला को स्पर्शरेखा रेखा का समीकरण देता है(t₀,t₀2). समीकरण t2 – 2tx + y = 0 y के लिए हमेशा x के फलन के रूप में हल किया जा सकता है और इसलिए, विचार करें}

$t^{2}-2tx+y(x)=0.\$

स्थानापन्न

$t=\left({\frac {dy}{dx}}\right)/2$

ode देता है

$\left({\frac {dy}{dx}}\right)^{2}\!\!-4x{\frac {dy}{dx}}+4y=0.$

आश्चर्य की बात नहीं y= 2tx− t² इस ODE के सभी समाधान हैं। चूँकि, रेखाओं के इस पैरामीटर समूह का आवरण है, जो परवलय y = x² है, इस ODE का भी समाधान है। एक अन्य प्रसिद्ध उदाहरण क्लेराट का समीकरण है।

आंशिक अंतर समीकरण

एनवलप का उपयोग पहले क्रम के आंशिक अंतर समीकरणों(पीडीई) के अधिक जटिल समाधानों को सरल लोगों से बनाने के लिए किया जा सकता है। मान लें कि F(x,u,Du) = 0 पहला ऑर्डर PDE है, जहां x एक वेरिएबल है जिसके मान खुले समूह Ω ⊂ 'R'ⁿ में हैं, u एक अज्ञात वास्तविक-मूल्यवान फलन है, Du, u का ढाल है, और F निरंतर भिन्न होने वाला फलन है जो Du में नियमित है। मान लीजिए कि u(x;a) समाधानों का एक m-पैरामीटर समूह है: अर्ताथ, प्रत्येक निश्चित a ∈ A ⊂ 'R' के लिए^m, u(x;a) अवकल समीकरण का एक हल है। अवकल समीकरण का नया समाधान पहले हल करके बनाया जा सकता है(यदि संभव हो तो)

$D_{a}u(x;a)=0\,$

x के फलन के रूप में a = φ(x) के लिए। फंक्शनों के समूह का एनवलप {u(·,a)}_a∈A द्वारा परिभाषित किया गया है

$v(x)=u(x;\varphi (x)),\quad x\in \Omega ,$

और अवकलन समीकरण को भी हल करता है(लेकिन यह एक निरंतर अवकलन फंक्शन के रूप में सम्मलित हो)।

ज्यामितीय रूप से, v(x) का ग्राफ़ हर जगह u(x;a) समूह के किसी सदस्य के ग्राफ़ पर स्पर्शरेखा है। चूँकि अवकल समीकरण प्रथम कोटि का है, यह केवल ग्राफ़ के स्पर्शरेखा तल पर एक शर्त रखता है, जिससे कि हर जगह किसी समाधान पर स्पर्श करने वाले किसी भी फलन का समाधान होना चाहिए। यही विचार मांगी शंकु के समाकलन के रूप में प्रथम कोटि के समीकरण के हल का आधार है। मांगी शंकु R^{(x,u) चरों के n+1} में एक शंकु क्षेत्र है प्रत्येक बिंदु पर पहले क्रम PDE के स्पर्शरेखा रिक्त स्थान के एनवलप द्वारा काटे गए। पीडीई का समाधान तब शंकु क्षेत्र का एक एनवलप है।

रिमेंनियन ज्यामिति में, यदि रीमैनियन कई गुना में एक बिंदु पी के माध्यम से जिओडेसिक्स के एक चिकनी समूह में एनवलप होता है, तो P के पास एक संयुग्मित बिंदु होता है जहां समूह के किसी भी जीओडेसिक ने एनवलप को काट दिया है। भिन्नताओं की कलन में समान रूप से अधिक सत्य है: यदि किसी दिए गए बिंदु P के माध्यम से एक फंक्शनात्मक के चरमपंथियों के एक समूह के पास एक एनवलप है, तो एक बिंदु जहां एनवलप को प्रतिच्छेदित करता है, वह P के लिए एक संयुग्मित बिंदु है।

कास्टिक

एक चक्र और समानांतर किरणों से उत्पन्न परावर्तक कास्टिक

ज्यामितीय प्रकाशिकी में, एक कास्टिक(प्रकाशिकी) किरण(प्रकाशिकी) के लिए उसके समूह का एनवलप है। इस चित्र में एक वृत्त का एक वृत्ताकार चाप है। प्रकाश किरणें(नीले रंग में दिखाई गई हैं) अनंत पर एक स्रोत से आ रही हैं, और इसलिए समानांतर पहुंचती हैं। जब वे वृत्ताकार चाप से टकराते हैं तो प्रकाश किरणें स्पेक्युलर परावर्तन के अनुसार अलग-अलग दिशाओं में बिखर जाती हैं। जब एक प्रकाश किरण के बिंदु पर चाप से टकराती है तो प्रकाश परावर्तित होगा जैसे कि यह उस बिंदु पर चाप की स्पर्श रेखा द्वारा परावर्तित किया गया हो। परावर्तित प्रकाश किरणें समतल में रेखाओं का एक-पैरामीटर समूह देती हैं। इन रेखाओं का आवरण कास्टिक(प्रकाशिकी) है। एक चिंतनशील कास्टिक में सामान्य रूप से चिकने वक्र बिंदु और पुच्छल(विलक्षणता) बिंदु सम्मलित होंगे।

भिन्नताओं की कलन के दृष्टिकोण से, फ़र्मेट के सिद्धांत(अपने आधुनिक रूप में) का तात्पर्य है कि प्रकाश किरणें फंक्शनात्मक लंबाई के लिए अतिवादी हैं

$L[\gamma ]=\int _{a}^{b}|\gamma '(t)|\,dt$

चिकनी समतल के बीच [a, b] पर निश्चित समापन बिंदु γ(a) और γ(b) के साथ। किसी दिए गए बिंदु P द्वारा निर्धारित कास्टिक(प्रतिबिम्ब में बिंदु अनंत पर है) P के संयुग्म बिंदुओं का समूह है।

ह्यूजेंस का सिद्धांत

प्रकाश एक प्रकाश किरण की दिशा और प्रारंभिक स्थिति के आधार पर अलग-अलग दरों पर एनिस्ट्रोपिक अमानवीय मीडिया से गुजर सकता है। बिंदुओं के समुच्चय की सीमा, जिस तक प्रकाश एक दिए गए बिंदु q से एक समय t के बाद यात्रा कर सकता है, को समय के बाद 't तरंग सामने के रूप में जाना जाता है, जिसे यहाँ Φ द्वारा निरूपित किया जाता है।_q(t)। इसमें ठीक वे बिंदु होते हैं जिन तक प्रकाश की गति से यात्रा करके 'q' से समय t में पहुंचा जा सकता है। ह्यूजेंस-फ्रेस्नेल सिद्धांत | ह्यूजेंस का सिद्धांत दावा करता है कि तरंग मोर्चा सेट है Φ_q0(s + t) तरंग मोर्चों के परिवार का एनवलप है Φ_q(s) क्ष ∈ Φ के लिए_{q0</उप>(टी)। अधिक सामान्यतः, बिंदु 'क्यू'0 अंतरिक्ष में किसी भी वक्र, सतह या बंद सेट द्वारा प्रतिस्थापित किया जा सकता है।}

यह भी देखें

• निहित सतह
• कास्टिक(गणित)

बाहरी संबंध

• Weisstein, Eric W. "Envelope". MathWorld.
• "Envelope of a family of plane curves" at MathCurve.