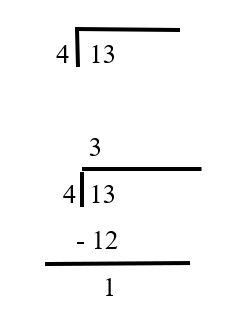परिकर्माष्टक- मूल संक्रिया: Difference between revisions

Latest revision as of 18:16, 29 November 2022

परिचय

अंकगणित , संख्याओं का उपयोग करके गणनाओं से संबोधित करना होता है। पाटीगणित , अंकगणित और ज्यामिति के लिए संस्कृत शब्द है। पाटीगणित शब्द पाटी(स्लेट) और गणित (गणित) को मिलाकर बना है। चूँकि एक स्लेट के बोर्ड का उपयोग करके गणित किया जाता था , इसलिए इसे पाटीगणित कहा जाता था। संख्याओं का उपयोग करने वाले सभी लेन-देन के लिए जोड़, घटाव, गुणा, भाग, वर्ग आदि के मूल संक्रिया की आवश्यकता होती है। प्राचीन भारतीय गणितज्ञों ने एक साथ आठ मूलभूत संक्रियाओं का उल्लेख किया है जिन्हें परिकर्माष्टक कहा जाता है।

परिभाषा

परिकर्म का अर्थ है अंकगणितीय संक्रियाएं और अष्टक का अर्थ है आठ का समूह। ^[1]

परिकर्माष्टक आठ बुनियादी कार्यों का प्रतीक है।

आठ मूल संक्रियाएँ इस प्रकार हैं:

संकलनम् (योग)
व्यावकलनम् (घटाव)
गुणन (गुणा)
भाजन (भाग)
वर्गः (वर्ग)
वर्गमूल (वर्गमूल)
घन (क्यूबिंग) और
घन-मूल (घनमूल)

जोड़ और घटाव सभी गणनाओं का आधार बनते हैं। नीचे दिए गए श्लोक में भास्कर प्रथम का उल्लेख है।

संयोगभेदा गुणनागतानि शुद्धेश्च भागो गतमूलमुक्तम् ।

व्याप्तं समीक्ष्योपचयक्षयाभ्यां विद्यादिदं द्व्यात्मकमेव शास्त्रम् ॥ (गणितपाद में आर्यभटीय भाष्य, पृष्ठ 43)

"सभी अंकगणितीय संचालन दो श्रेणियों में हल होते हैं, हालांकि आमतौर पर चार माने जाते हैं। दो मुख्य श्रेणियां वृद्धि और कमी हैं। जोड़ बढ़ाया जाता है और घटाव घटाया जाता है। संचालन की ये दो किस्में पूरे गणित में व्याप्त हैं। गुणन और वृद्धि (वर्ग आदि) विशेष प्रकार के जोड़ हैं; और विभाजन और प्रत्यावर्तन(वर्गमूल, आदि) विशेष प्रकार के घटाव हैं। वास्तव में प्रत्येक गणितीय संक्रिया को वृद्धि या कमी के रूप में मान्यता दी जाती है। इसलिए इस पूरे विज्ञान को सही मायने में इन दोनों से मिलकर ही पहचाना जाना चाहिए।"^[2]

संकलन और व्यावकलन (जोड़ और घटाव)

जोड़

जोड़, गणित ^[3]में पहली मूल संक्रिया है। घटाव, जोड़ का उल्टा है।

आर्यभट द्वितीय (950) जोड़ को "कई संख्याओं में से एक बनाना जोड़ है" के रूप में परिभाषित करते हैं।

आर्यभट द्वितीय (950) घटाव को "सर्वधन (कुल) से (कुछ संख्या का) निकालना घटाव है" के रूप में परिभाषित करते हैं । जो बचता है उसे शेष (बचा हुआ अंश)" कहा जाता है।

भास्कर द्वितीय ने लीलावती पर अपने काम में इन कार्यों का उल्लेख किया है।

कार्यः क्रमादुत्क्रमतोऽथवाऽङ्कयोगो यथास्थानकमन्तरं वा ॥ (लीलावती , बनाम 12, पृ.12)

"जोड़ या घटाव (दी गई संख्याओं में अंकों का) स्थान के अनुसार दाएं से बाएं या बाएं से दाएं किया जाना होता है।"

दी गई संख्याओं को एक दूसरे के नीचे इस प्रकार लिखिए कि अंक उनके स्थानीय मान के अनुरूप हों। फिर इकाइयों के स्थान से शुरू करके अंकों को जोड़ें या घटाएँ, बाद में दहाई पर जाएँ, और इसी तरह आगे भी।

जोड़ के लिए संस्कृत नाम - योग (जोड़), संयोग (योग), संयोजना (एक साथ जुड़ना), संयुति (योग), संयुति (योग), संकलन (एक साथ बनाना)।

घटाव के लिए संस्कृत नाम - व्युतकलिता (अलग किया गया), व्युतकलाना (अलग करना), शोधन (समाशोधन), पाटन (गिरने का कारण), वियोग (पृथक्करण), शेष (अवशेष) और अनतर (अंतर) का उपयोग शेष के लिए किया गया है।

गुणन (गुणा)

पूर्ण संख्याओं का गुणन, उनका जोड़ दोहराया जाना जाता होता है।। उदाहरण के लिए :

$2\quad X\quad 4=2+2+2+2=8$

गुणन के लिए संस्कृत नाम - आहती (गुणा), घट (गुणनफल), [गुणन, हनन, हति, वध ] (गुणा)।


2	X	4	=	8
↑		↑		↑
गुण्य (गुण्य जिस को किसी संख्या से गुणा किया जाय)		गुणक (गुणक)		गुणनफल (गुणन का परिणाम)

गुणन के तरीके:

रूप-गुणन - प्रत्यक्ष विधि
खण्ड -गुणन - विभाजन विधि
भक्त-गुणन - कारक विधि
स्थान-विभाग-गुणन - स्थानवार गुणन
इष्टानुयोग-गुणन (इच्छित संख्या जोड़ना या घटाना)

रूप-गुणन - प्रत्यक्ष विधि:

यहां गुणक की सारणी ज्ञात होनी चाहिए। गुणक को समग्र रूप में लिया जाता है। गुणक के प्रत्येक अंक को गुणक से गुणा करके गुणनफल प्राप्त किया जाता है। इस पद्धति में, गुणक को छोटा होने के कारण पूर्ण लिया जाता है।

उदाहरण: 234 X 5 =

(1) (2)

2 3 4

x 5 =

1 1 7 0

खण्ड -गुणन - विभाजन विधि:

यहाँ गुणक को दो संख्याओं के योग में विभाजित किया जाता है। इसे नीचे के रूप में दर्शाया गया है।

a X b = a X (c + d) = (a X c) + (a X d) जहां पे b = c + d.

यह जोड़ पर गुणन का वितरण गुण है।

उदाहरण: 234 X 16 = 234 X (10 + 6 ) = (234 X 10) + (234 X 6) = 2340 + 1404 = 3744

भक्त-गुणन - कारक विधि:

यहाँ गुणक को दो संख्याओं के योग में विभाजित किया जाता है। यह नीचे दर्शाया गया है।

a X b = a X (c X d) = (a X c) X d जहां पे b = c X d

उदाहरण: 234 X 16 = 234 X (8 X 2) = (234 X 8) X 2 = 1872 X 2 = 3744

स्थान-विभाग-गुणन - स्थानवार गुणन:

गुणा

गुणक के प्रत्येक अंक से गुण्य को अलग से गुणा करें। उन्हें उचित रूप से एक के नीचे एक रखें। उन अंकों को जोड़ें। यह विधि गुणन करने की मानक विधि है।

उदाहरण: 234 X 16

2 3 4

X 1 6 =

1 4 0 4

+ 2 3 4 =

3 7 4 4

इष्टानुयोग-गुणन (इच्छित संख्या जोड़ना या घटाना):

संस्कृत शब्द इष्टानुयोग एक मिश्रित शब्द है जिसमें इष्टा, ऊन, युक शामिल है जिसका अर्थ क्रमशः 'वांछित, ऋण और लाभ' है।

इष्टोनयुक्तेन गुणेन निघ्नोऽभीष्टघ्नगुण्यान्वितवर्जितो वा । (लीलावती, बनाम 16, पृ.15)

"गुणक में किसी भी सुविधाजनक संख्या को जोड़ें या घटाएं और इसे गुणा करें। फिर जोड़ी गई या घटाई गई संख्या से गुणा करें और इस गुणनफल को पिछले वाले से घटाएं या जोड़ें।"

उचित पूर्ण अंक प्राप्त करने के लिए गुणक में कोई भी वांछित संख्या जोड़ें। फिर गुणक को पूर्ण अंक और जोड़ी गई संख्या से गुणा करें। फिर अंतिम उत्तर पाने के लिए गुणनफल को घटाएं।

या

उचित पूर्ण अंक प्राप्त करने के लिए गुणक से कोई वांछित संख्या घटाएं। फिर गुणक को पूर्ण अंक और घटाई गई संख्या से गुणा करें। फिर अंतिम उत्तर पाने के लिए गुणनफल को जोड़ें।

उदाहरण:

234 X 16 = 234 X (20 - 4) = (234 X 20) - (234 X 4) = 4680 - 936 = 3744

234 X 16 = 234 X (10 + 6) = (234 x 10) + (234 x 6) = 2340 + 1404 = 3744

तटस्थ-गुणन:

प्राचीन भारतीय गणितज्ञों ने गुणन को अधिक कुशलतापूर्वक और आसानी से करने के लिए गुणन के कई तरीकों को बढ़ाया है। तटस्थ-गुणन उन विधियों में से एक है जिसमें तीन या अधिक अंकों को तेजी से गुणा करना शामिल है। श्रीधर, महावीर, और श्रीपति जैसे भारतीय गणितज्ञों ने इस पद्धति का उल्लेख किया है। तटस्थ-गुणन को वज्रभ्यास के नाम से भी जाना जाता है।

गणेश (सी.1545) तटस्थ-गुणन की व्याख्या इस प्रकार करते हैं, "गुणन की वह विधि जिसमें संख्याएँ एक ही स्थान पर खड़ी होती हैं, तटस्थ-गुणन कहलाती है। यह इस प्रकार है: गुण्य के तहत गुणक को नियुक्त करने के बाद इकाई द्वारा गुणा करें और नीचे परिणाम टिप्पणी/नोट करें। फिर जैसा कि वज्रभ्यास में किया जाता है, इकाई से दस और दस से गुणा करें, एक साथ जोड़ें, और परिणाम को पंक्ति में नियुक्त करें। अगली इकाई को सौ से, सौ से इकाई और दस को दस से गुणा करें, एक साथ जोड़ें और परिणाम को पहले की तरह नियुक्त करें; और इसी तरह बाकी अंकों के साथ। ऐसा किया जाने के बाद ,परिणामों की पंक्ति गुणनफल होती है।"

यह विधि 8वीं शताब्दी या उससे पहले के हिंदू विद्वानों को ज्ञात थी। ऐसा लगता है कि विधि अरब की यात्रा कर चुकी है और वहां से यूरोप को प्रेषित की गई थी, जहां यह पैसीओली के सुमा में होती है और इसे "दूसरों की तुलना में अधिक शानदार और सरल" कहा जाता है।

गणेश ने यह भी टिप्पणी की है कि "यह (विधि) बहुत अद्भुत है और पारंपरिक मौखिक निर्देशों के बिना सुस्त द्वारा नहीं सीखा जा सकता है।"

उदाहरण:

234 और 15 का गुणा करें

2 3 5

0 1 5 X


सैकड़ों	दसियों	इकाई
2	3	4
0	1	5

इकाई अंक को इकाई अंक से गुणा करें। 4 X 5 = 20
इकाई के अंक को दहाई के अंक से और दहाई के अंक को इकाई के अंक से गुणा करें और उन्हें जोड़ दें। (3 X 5) + (4 X 1) = 15 + 4 = 19
इकाई अंक को सैकड़ा अंक से, सैकड़ा अंक को इकाई अंक से और दहाई के अंक को दहाई के अंक से गुणा करें और उन्हें जोड़ दें। (2 x 5) + (4 X 0) + (3 X 1) = 10 + 0 + 3 = 13
सैकड़ों अंकों को दहाई के अंक से और दहाई के अंक को सैकड़ों अंकों से गुणा करें और उन्हें जोड़ दें। (2 X 1) + (3 X 0) = 2 + 0 = 2 = 02
सौ अंकों को सौ अंकों से गुणा करें। 2 X 0 = 0 = 00
दिखाए गए अनुसार प्रत्येक उपाय के परिणाम रखें और जोड़ें।


1.					2	0
2.				1	9
3.			1	3
4.		0	2
5.	0	0
	0	0	3	5	1	0

परिणाम 3510 है।

भाजन (भाग)

भाग

भाग को गुणन का विलोम माना जाता है।^[4]

विभाजन के लिए संस्कृत नाम - भागाहार (विभाजित करना),भाजन (विराम), हरण (शेष निकालना), छेदना (कटौती करना)।

लाभांश को भाज्य या हार्य कहा जाता है, भाजक को भाजक, भागहार, या हार कहा जाता है। भागफल को लब्धी (प्राप्त) या लब्ध कहा जाता है। भास्कर द्वितीय ने विभाजन के नियम का उल्लेख इस प्रकार किया है:

भाज्याद्धरः शुद्ध्यति यद्गुणः स्यादन्त्यात्फलं तत्खलु भागहारे। समेन केनाप्यपवर्त्य हारभाज्यौ भवेद्वा सति सम्भवे तु ॥ (लीलावती, बनाम 18, पृ.18)

"विभाजित के अंतिम अंक से शुरू करके, (अधिकतम) जितनी बार भाजक को घटाया जा सकता है, वह वास्तव में भागफल (भाग का परिणाम) है।

यदि संभव हो तो भाजक और लाभांश में कुछ सामान्य कारक को रद्द करने के बाद विभाजित करें।"

भास्कर द्वितीय ने विभाजन की नियमित विधि के साथ उल्लेख किया है, उन्होंने परिणाम प्राप्त करने के लिए भाजक और लाभांश के सामान्य कारकों को हटाने की विधि का वर्णन किया है।

उदाहरण ${\frac {748}{108}}={\frac {748/4}{108/4}}={\frac {187}{27}}={\frac {Bhajya}{Bhajaka}}=Labdhi(6)$

वर्गः(वर्ग)

वर्ग, वर्गः या कृति के लिए संस्कृत नाम है। वर्ग शब्द का अर्थ है "पंक्तियाँ" या समान चीजों का एक समूह। लेकिन गणित में यह वर्ग घात और वर्ग आकृति या उसके क्षेत्रफल को भी दर्शाता है। आर्यभट प्रथम कहते हैं : "चार बराबर भुजाओं वाली एक वर्ग आकृति और (इसके क्षेत्रफल को प्रतिनिधित्व करने वाली संख्या) वर्ग कहलाती है। दो समान मात्राओं का गुणनफल भी वर्ग होता है।"

भास्कर प्रथम ने वर्ग ज्ञात करने की एक विधि इस प्रकार दी है:

"वर्गीकरण के नियम के अनुसार, अंतिम अंक (सबसे बाईं ओर) का वर्ग करें, शेष सभी अंकों को अंतिम अंक से दोगुना करें, एक अंक को दाईं ओर स्थानांतरित करके(पहला अंक आने तक) प्रक्रिया को दोहराएं । उदाहरण: 6387 का वर्ग =40793769

उपाय 4.1 के बाद प्रत्येक कॉलम में संख्याएँ जोड़ें। जहाँ भी दो अंक हों। इकाई अंक बरकरार रखा जाना है। दसवें स्थान के अंक को बाईं ओर के अगले कॉलम में ले जाकर जोड़ा जाना है। यहां एक इकाई अंक भी रखा जाना है। दसवें स्थान के अंक को बाईं ओर के अगले कॉलम में ले जाना है और जोड़ना है। इसी तरह आगे करते रहें ।


		40	7	9	3	7	6	9
Step		39	15	27	23	7	6	9
4.1	7²						4	9
3.2	2 x 8 x 7				1	1	2
3.1	8²				6	4
2.3	2 x 3 x 7				4	2
2.2	2 x 3 x 8			4	8
2.1	3²			9
1.4	2 x 6 x 7			8	4
1.3	2 x 6 x 8		9	6
1.2	2 x 6 x 3	3	6
1.1	6²	36
1	दी गई संख्या	6	3	8	7
2	संख्या को दाईं ओर परिवर्तित करें		6	3	8	7
3	संख्या को दाईं ओर परिवर्तित करें			6	3	8	7
4	संख्या को दाईं ओर परिवर्तित करें				6	3	8	7

वर्गमूल (वर्गमूल)

वर्ग और वर्गमूल

वर्गमूल का संस्कृत नाम वर्गमूल है। मूल, पद का मतलब हिंदू शब्दावली में जड़ है। करणी शब्द शुलबसूत्रों में वर्गमूल के लिए एक शब्द के रूप में पाया जाता है।

आर्यभटीय में वर्गमूल ज्ञात करने की विधि इस प्रकार दी गई है "हमेशा सम स्थान को वर्गमूल के दोगुने से विभाजित करें (पूर्ववर्ती विषम स्थान तक); विषम स्थान से वर्ग (भागफल का) घटाने के बाद, भागफल अगले स्थान पर (मूल की पंक्ति में) डालने से मूल मिलता है"

उदाहरण: 956484 का वर्गमूल = 978


		अवर्ग	वर्ग	अवर्ग	वर्ग	अवर्ग	वर्ग
		9	5	6	4	8	4
वर्ग से घटाना = 9²		8	1					मूल = 9
मूल से दोगुने से भाग दें = 2 x 9 =18	18	1	4	6	7			मूल = 97
		1	2	6
			2	0	4
भागफल के वर्ग से घटाना = 72 = 49				4	9
मूल से दोगुने से भाग दें = 2 x 97 = 194	194		1	5	5	8	8	मूल = 978
			1	5	5	2
						6	4
भागफल के वर्ग से घटाना = 82 = 64	64					6	4
							0

घन (क्यूब )

घन - घनमूल

घन का संस्कृत नाम घन, वृंदा है।

भास्कर द्वितीय ने किसी संख्या का घन ज्ञात करने के नियम का उल्लेख इस प्रकार किया है।

अंतिम का घन नियुक्त करें; तो अंतिम का वर्ग उत्तरवर्ती के तीन गुना से गुणा किया जाता है;फिर उत्तरवर्ती के वर्ग को अंतिम के तीन गुना से गुणा किया जाता है और फिर उत्तरवर्ती का घन को ; इन्हें इसलिए रखा जाता है ताकि एक परिणाम और अगले के बीच एक स्थान का अंतर हो और जोड़ द्वारा घन दिया जाए।

दी गई संख्या को स्थानों के अनुसार भागों में बाँटा जाता है, जिनमें से एक को अंतिम के लिए लिया जाता है और अगले को पहले के रूप में और इसी तरह दोहराते हुए (यदि अवसर हो)।

या फिर घन को खोजने के लिए आंकड़ों के पहले स्थान से भी यही प्रक्रिया शुरू की जा सकती है।"

उदाहरण: 1234 के घन में चार स्थान हैं जैसा कि नीचे दिखाया गया है। प्रारंभ में, हम अंतिम अंक 1 और उसके बाद के अंक 2 यानी 12 को लेते हैं और घन /क्यूबिंग की विधि लागू करते हैं


1	2	3	4


	1	2
अंतिम अंक का घन	1
अंतिम अंक के वर्ग का तिगुना (3 x 1²) उत्तरवर्ती से गुणा किया गया अंक (2) 2 x 3 x 1² है और अगले स्थान पर रखा गया है		6
अगले अंक के वर्ग का तिगुना (2) गुणा अंतिम अंक से 3 x 2² x 1 है और अगले स्थान पर रखा गया है		1	2
अगले अंक का घन (2³)				8
12 का घन = उपरोक्त अंकों का योग	1	7	2	8

इसके बाद, हम अगला अंक 3 लेंगे यानी संख्या 123 है। यहां 12 अंतिम अंक है और 3 अगला अंक है। विधि इस प्रकार जारी है।

			12	3
अंतिम अंक -12 का घन (पहले से ही प्राप्त)	1	7	2	8
अंतिम अंक के वर्ग का तिगुना (3 x 12²) सक्सेसिंग से गुणा किया जाता है अंक (3) 3 x 3 x 12² है और अगले स्थान पर रखा गया है		1	2	9	6
अगले अंक के वर्ग का तिगुना (3)गुणा अंतिम अंक से 3 x 3² x 12 है और अगले स्थान पर रखा गया है				3	2	4
अगले अंक का घन (3³)						2	7
123 का घन = उपरोक्त अंकों का योग	1	8	6	0	8	6	7

अब शेष अंक 4 को इस प्रकार लिया जाता है कि संख्या 1234 हो जिसमें से 123 अंतिम अंक हो और 4 अगला अंक हो। विधि इस प्रकार जारी है।

			123	4
अंतिम अंक का घन -123 (पहले से ही प्राप्त)	1	8	6	0	8	6	7
अंतिम अंक के वर्ग का तिगुना (3 x 123²) सक्सेसिंग से गुणा किया जाता है अंक (4) 4 x 3 x 123² है और इसे अगले स्थान पर रखा गया है			1	8	1	5	4	8
अगले अंक के वर्ग का तिगुना (4) गुणा अंतिम अंक से 3 x 4² x 123 है और अगले स्थान पर रखा गया है						5	9	0	4
अगले अंक का घन (4³)									6	4
1234 का घन = उपरोक्त अंकों का योग	1	8	7	9	0	8	0	9	0	4

घन-मूल (घनमूल)

घनमूल का संस्कृत नाम घन-मूल, घन-पद है।

आर्यभटीय में घनमूल(क्यूब-रूट) के संचालन का विवरण दिया गया है "दूसरा अघन स्थान को घनमूल के वर्ग से तीन बार विभाजित करें; पहले अघन स्थान से घटाएं भागफल के वर्ग को तीन बार पूर्ववर्ती घनमूल से गुणा किया जाता है। ); और (घटाना) घन (भागफल का) घन स्थान से; (भागफल को अगले स्थान पर (मूल की पंक्ति में) नीचे रखा जाता है, जड़ देता है)"। 2628072 का घनमूल 138 है।


		घन	अघन	अघन	घन	अघन	अघन	घन	मूल
		2	6	2	8	0	7	2
घटाना 1³		1							1
3 x 1² से भाग	3	1	6	3 - भागफल					13
			9
			7	2
घटाना 3 x 1 x 3²			2	7
			4	5	8
घटाना 3³				2	7
3 x 13² से भाग	507		4	3	1	0	8 -भागफल		138
			4	0	5	6
				2	5	4	7
घटाना 3 x 13 x 8²				2	4	9	6
						5	1	2
घटाना 8³						5	1	2
								0

बाहरी संपर्क

यह भी देखें

Parikarmāṣṭaka - Fundamental Operations

संदर्भ

↑ भारतीय गणितम के लिए एक प्राइमर, भारतीय-गणित-प्रवेश- भाग -1, नई दिल्ली: संस्कृत प्रमोशन फाउंडेशन(A Primer to Bhāratīya Gaṇitam , Bhāratīya-Gaṇita-Praveśa- Part-1. New Delhi: Samskrit Promotion Foundation.) 2021. ISBN 978-81-951757-2-7.
↑ दत्ता, विभूतिभूषण; नारायण सिंह, अवधेश (1962)। हिंदू गणित का इतिहास। मुंबई: एशिया पब्लिशिंग हाउस।(Datta, Bibhutibhusan; Narayan Singh, Avadhesh (1962). History of Hindu Mathematics. Mumbai: Asia Publishing House.)
↑ मौलिक-संचालन-पूर्णांक/(fundamental-operations-integers/)
↑ गुणन के प्रतिलोम के रूप में भाग(Division-as-The-Inverse-of-Multiplication)

[1] भारतीय गणितम के लिए एक प्राइमर, भारतीय-गणित-प्रवेश- भाग -1, नई दिल्ली: संस्कृत प्रमोशन फाउंडेशन(A Primer to Bhāratīya Gaṇitam , Bhāratīya-Gaṇita-Praveśa- Part-1. New Delhi: Samskrit Promotion Foundation.) 2021. ISBN 978-81-951757-2-7.

[2] दत्ता, विभूतिभूषण; नारायण सिंह, अवधेश (1962)। हिंदू गणित का इतिहास। मुंबई: एशिया पब्लिशिंग हाउस।(Datta, Bibhutibhusan; Narayan Singh, Avadhesh (1962). History of Hindu Mathematics. Mumbai: Asia Publishing House.)

[3] मौलिक-संचालन-पूर्णांक/(fundamental-operations-integers/)

[4] गुणन के प्रतिलोम के रूप में भाग(Division-as-The-Inverse-of-Multiplication)

[1]

[2]

[3]

[4]

@@ Line 7: / Line 7: @@
 == परिभाषा ==
-''परिकर्म''  का अर्थ है अंकगणितीय संक्रियाएं और ''अष्टक'' का अर्थ है आठ का समूह। <ref>''A Primer to Bhāratīya Gaṇitam , Bhāratīya-Gaṇita-Praveśa- Part-1''. New Delhi: Samskrit Promotion Foundation. 2021. [[ISBN (identifier)|ISBN]] [[Special:BookSources/978-81-951757-2-7|<bdi>978-81-951757-2-7</bdi>]].</ref>
+''परिकर्म''  का अर्थ है अंकगणितीय संक्रियाएं और ''अष्टक'' का अर्थ है आठ का समूह। <ref>भारतीय गणितम के लिए एक प्राइमर, भारतीय-गणित-प्रवेश- भाग -1, नई दिल्ली: संस्कृत प्रमोशन फाउंडेशन(''A Primer to Bhāratīya Gaṇitam , Bhāratīya-Gaṇita-Praveśa- Part-1''. New Delhi: Samskrit Promotion Foundation.) 2021. [[ISBN (identifier)|ISBN]] [[Special:BookSources/978-81-951757-2-7|<bdi>978-81-951757-2-7</bdi>]].</ref>
 ''परिकर्माष्टक'' आठ बुनियादी कार्यों का प्रतीक है।
@@ Line 28: / Line 28: @@
 ''व्याप्तं समीक्ष्योपचयक्षयाभ्यां विद्यादिदं द्व्यात्मकमेव शास्त्रम् ॥'' <small>(गणितपाद में आर्यभटीय भाष्य, पृष्ठ 43)</small>
-"सभी अंकगणितीय संचालन दो श्रेणियों में हल होते हैं, हालांकि आमतौर पर चार माने जाते हैं। दो मुख्य श्रेणियां वृद्धि और कमी हैं। जोड़ बढ़ाया जाता है और घटाव घटाया जाता है। संचालन की ये दो किस्में पूरे गणित में व्याप्त हैं। गुणन और वृद्धि (वर्ग आदि) विशेष प्रकार के जोड़ हैं; और विभाजन और  प्रत्यावर्तन(वर्गमूल, आदि) विशेष प्रकार के घटाव हैं। वास्तव में प्रत्येक गणितीय संक्रिया को वृद्धि या कमी के रूप में मान्यता दी जाती है। इसलिए इस पूरे विज्ञान को सही मायने में इन दोनों से मिलकर ही पहचाना जाना चाहिए।"<ref>Datta, Bibhutibhusan; Narayan Singh, Avadhesh (1962). ''History of Hindu Mathematics''. Mumbai: Asia Publishing House.</ref>
+"सभी अंकगणितीय संचालन दो श्रेणियों में हल होते हैं, हालांकि आमतौर पर चार माने जाते हैं। दो मुख्य श्रेणियां वृद्धि और कमी हैं। जोड़ बढ़ाया जाता है और घटाव घटाया जाता है। संचालन की ये दो किस्में पूरे गणित में व्याप्त हैं। गुणन और वृद्धि (वर्ग आदि) विशेष प्रकार के जोड़ हैं; और विभाजन और  प्रत्यावर्तन(वर्गमूल, आदि) विशेष प्रकार के घटाव हैं। वास्तव में प्रत्येक गणितीय संक्रिया को वृद्धि या कमी के रूप में मान्यता दी जाती है। इसलिए इस पूरे विज्ञान को सही मायने में इन दोनों से मिलकर ही पहचाना जाना चाहिए।"<ref>दत्ता, विभूतिभूषण; नारायण सिंह, अवधेश (1962)। हिंदू गणित का इतिहास। मुंबई: एशिया पब्लिशिंग हाउस।(Datta, Bibhutibhusan; Narayan Singh, Avadhesh (1962). ''History of Hindu Mathematics''. Mumbai: Asia Publishing House.)</ref>
 == संकलन और व्यावकलन (जोड़ और घटाव) ==
 [[File:Addition.svg|thumb|235x235px|जोड़]]
-जोड़, [[गणित का विकास|गणित]] <ref>[https://www.aplustopper.com/fundamental-operations-integers/ fundamental-operations-integers/]</ref>में पहली मूल संक्रिया है। घटाव, जोड़ का उल्टा है।
+जोड़, [[गणित का विकास|गणित]] <ref>मौलिक-संचालन-पूर्णांक/([https://www.aplustopper.com/fundamental-operations-integers/ fundamental-operations-integers/])</ref>में पहली मूल संक्रिया है। घटाव, जोड़ का उल्टा है।
-[[आर्यभट्ट|आर्यभट्ट द्वितीय]] (950) जोड़ को "कई संख्याओं में से एक बनाना जोड़ है" के रूप में परिभाषित करते हैं।
+[[आर्यभट्ट|आर्यभट द्वितीय]] (950) जोड़ को "कई संख्याओं में से एक बनाना जोड़ है" के रूप में परिभाषित करते हैं।
-आर्यभट्ट द्वितीय (950) घटाव को "''सर्वधन'' (कुल) से (कुछ संख्या का) निकालना घटाव है" के रूप में  परिभाषित करते हैं । जो बचता है उसे ''शेष'' (बचा हुआ अंश)" कहा जाता है।
+आर्यभट द्वितीय (950) घटाव को "''सर्वधन'' (कुल) से (कुछ संख्या का) निकालना घटाव है" के रूप में  परिभाषित करते हैं । जो बचता है उसे ''शेष'' (बचा हुआ अंश)" कहा जाता है।
 [[भास्कर द्वितीय]] ने लीलावती पर अपने काम में इन कार्यों का उल्लेख किया है।
@@ Line 245: / Line 245: @@
 == भाजन (भाग) ==
 [[File:Division 13-4.png|thumb|भाग]]
-भाग को गुणन का विलोम माना जाता है।<ref>[https://www.math-only-math.com/Division-as-The-Inverse-of-Multiplication.html Division-as-The-Inverse-of-Multiplication]</ref>
+भाग को गुणन का विलोम माना जाता है।<ref>गुणन के प्रतिलोम के रूप में भाग([https://www.math-only-math.com/Division-as-The-Inverse-of-Multiplication.html Division-as-The-Inverse-of-Multiplication])</ref>
 विभाजन के लिए संस्कृत नाम - ''भागाहार'' (विभाजित करना),''भाजन'' (विराम), ''हरण'' (शेष निकालना), ''छेदना'' (कटौती करना)।
@@ Line 896: / Line 896: @@
 == यह भी देखें ==
-[[Parikarmastaka - Fundamental Operations]]
+[[Parikarmāṣṭaka - Fundamental Operations]]
 == संदर्भ ==
 <references />
+[[Category:Articles using infobox templates with no data rows]]
+[[Category:Articles with hCards]]
 [[Category:Machine Translated Page]]
+[[Category:Organic Articles]]
-[[Category:Vigyan Ready]]
 [[Category:अंकगणित]]
 [[Category:गणित]]

Anonymous

Search

परिकर्माष्टक- मूल संक्रिया: Difference between revisions

Namespaces

More

Page actions

Latest revision as of 18:16, 29 November 2022

Contents

परिचय

परिभाषा

संकलन और व्यावकलन (जोड़ और घटाव)