K-माध्यम क्लस्टरिंग: Difference between revisions
No edit summary |
No edit summary |
||
| (20 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Vector quantization algorithm minimizing the sum of squared deviations}} | {{Short description|Vector quantization algorithm minimizing the sum of squared deviations}}K-माध्यम [[वेक्टर परिमाणीकरण|संचालन परिमाणीकरण]] की विधि है, जो मूल रूप से [[ संकेत आगे बढ़ाना |संकेत को आगे बढ़ाता]] है, जिसका उद्देश्य उपसमुच्चय ''N'' अवलोकनों को ''K'' माध्यमों में विभाजित करना है जिसमें प्रत्येक अवलोकन [[क्लस्टर (सांख्यिकी)|माध्यम (सांख्यिकी)]] से संबंधित हैI निकटतम माध्य (माध्यम केंद्र या माध्यम [[केन्द्रक]]) के साथ, माध्यम के प्रोटोटाइप के रूप में कार्य करता है। इसका परिणाम वोरोनोई कोशिकाओं में डेटा स्थान के विभाजन में होता है। ''k''-अर्थात माध्यम भिन्नता को अल्प करता है, किन्तु नियमित यूक्लिडियन दूरियों को नहीं, जो कि अधिक कठिन [[वेबर समस्या]] होगी I माध्य त्रुटियों का अनुकूलन करता है, जबकि केवल ज्यामितीय माध्य यूक्लिडियन दूरी को अल्प करता है। उदाहरण के लिए, उत्तम यूक्लिडियन समाधान k-मेडियन और k-मेडोइड्स का उपयोग करके पाया जा सकता है। | ||
समस्या कम्प्यूटेशनल रूप से कठिन है ([[एनपी-कठोरता]]) चूंकि, कुशल अनुमानी एल्गोरिदम [[स्थानीय इष्टतम]] में परिवर्तित हो जाते हैं। ये सामान्यतः 'K-साधन' एवं 'गाऊसी [[मिश्रण मॉडल|मिश्रण]] प्रारूपो' दोनों द्वारा नियोजित पुनरावृत्त शोधन दृष्टिकोण के माध्यम से गॉसियन वितरण के मिश्रण प्रारूप के लिए अपेक्षा-अधिकतमकरण एल्गोरिथ्म के समान हैं। वे दोनों डेटा को प्रारूप करने के लिए माध्यम केंद्रों का उपयोग करते हैं; चूंकि, '' k''- का [[अर्थ]] है माध्यमिंग तुलनीय स्थानिक सीमा के माध्यमों का शोध करने के लिए किया जाता है, जबकि गॉसियन मिश्रण प्रारूप माध्यम्स को भिन्न-भिन्न आकार देने की अनुमति देता है। | |||
अनियंत्रित ''k''-अर्थात एल्गोरिदम का k-निकटतम परस्पर से संबंध है, ''k''-निकटतम परस्पर वर्गीकारक, के लिए लोकप्रिय पर्यवेक्षित[[ यंत्र अधिगम ]]प्रविधि है, अर्थात नाम के कारण जिसे प्रायः भ्रमित किया जाता है। ''K'' द्वारा प्राप्त माध्यम केंद्रों में 1-निकटतम परस्पर वर्गीकारक को प्रारम्भ करने का अर्थात उपस्थित माध्यम में नए डेटा को वर्गीकृत करना है। इसे [[निकटतम केन्द्रक वर्गीकारक]] या [[रोक्चियो एल्गोरिथम]] के रूप में जाना जाता है। | |||
== विवरण == | |||
टिप्पणियों के उपसमुच्चय को देखते हुए (x<sub>1</sub>, x<sub>2</sub>, ..., x<sub>''n''</sub>), जहां प्रत्येक अवलोकन डी-आयामी वास्तविक सदिश है, k-अर्थात माध्यमिंग का उद्देश्य n अवलोकनों को k (≤ n) समुच्चय 's' = {s में विभाजित करना है<sub>1</sub>, s<sub>2</sub>, ..., s<sub>k</sub>} जिससे वर्गों के अंदर-माध्यम योग (WCSS) (अर्थात विचरण) को अल्प किया जा सके। औपचारिक रूप से इस उद्देश्य का शोध करना हैI <div वर्ग = केंद्र><math>\underset{\mathbf{S}} {\operatorname{arg\,min}} \sum_{i=1}^{k} \sum_{\mathbf x \in S_i} \left\| \mathbf x - \boldsymbol\mu_i \right\|^2 = \underset{\mathbf{S}} {\operatorname{arg\,min}} \sum_{i=1}^k |S_i| \operatorname{Var} S_i </math>जहां ''μ<sub>i</sub> में बिंदुओं का माध्य <math>S_i</math> (जिसे केन्द्रक भी कहा जाता है) है , अर्थात'' <डिव वर्ग = केंद्र> | |||
<math>\boldsymbol{\mu_i} = \frac{1}{|S_i|}\sum_{\mathbf x \in S_i} \mathbf x, </math> | |||
<math>|S_i|</math> का आकार <math>S_i</math> है , एवं <math>\|\cdot\| </math> सामान्य L<sup>2</sup> मानदंड (गणित) है| | <math>|S_i|</math> का आकार <math>S_i</math> है , एवं <math>\|\cdot\| </math> सामान्य L<sup>2</sup> मानदंड (गणित) है| | ||
यह | |||
यह माध्यम में बिंदुओं के जोड़ीदार वर्ग विचलन को अल्प करने के बराबर है<math>\underset{\mathbf{S}} {\operatorname{arg\,min}} \sum_{i=1}^{k} \, \frac{1}{ |S_i|} \, \sum_{\mathbf{x}, \mathbf{y} \in S_i} \left\| \mathbf{x} - \mathbf{y} \right\|^2</math> | |||
== इतिहास == | == इतिहास == | ||
k-माध्यिका शब्द का प्रथम बार उपयोग जेम्स मैकक्वीन ने 1967 में किया था।<ref name="macqueen19672">{{cite conference |last=MacQueen |first=J. B. |year=1967 |title=बहुभिन्नरूपी टिप्पणियों के वर्गीकरण और विश्लेषण के लिए कुछ विधिया होती है। |url=http://projecteuclid.org/euclid.bsmsp/1200512992 |conference=Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability |publisher=University of California Press |volume=1 |pages=281–297 |mr=0214227 |zbl=0214.46201 |access-date=2009-04-07 }}</ref> चूँकि यह विचार 1956 में [[ह्यूगो स्टीनहॉस]] के पास वापस चला गया।<ref>{{cite journal |last=Steinhaus |first=Hugo |author-link=Hugo Steinhaus |year=1957 |title=Sur la division des corps matériels en parties |journal=Bull. Acad. Polon. Sci. |language=fr |volume=4 |issue=12 |pages=801–804 |mr=0090073 |zbl=0079.16403 }}</ref> मानक एल्गोरिथम प्रथम बार 1957 में [[बेल लैब्स]] के स्टुअर्ट लॉयड द्वारा [[ पल्स कोड मॉडुलेशन | पल्स कोड मॉडुलेशन]] के लिए प्रविधियों के रूप में प्रस्तावित किया गया था, चूँकि इसे 1982 तक जर्नल लेख के रूप में प्रकाशित नहीं किया गया था।<ref name="lloyd19572">{{cite journal |last=Lloyd |first=Stuart P. |year=1957 |title=पीसीएम में अल्प से अल्प वर्ग परिमाणीकरण होते है|journal=Bell Telephone Laboratories Paper }} Published in journal much later: {{cite journal |last=Lloyd |first=Stuart P. |year=1982 |title=Least squares quantization in PCM |url=http://www.cs.toronto.edu/~roweis/csc2515-2006/readings/lloyd57.pdf |journal=[[IEEE Transactions on Information Theory]] |volume=28 |issue=2 |pages=129–137 |doi=10.1109/TIT.1982.1056489 |access-date=2009-04-15 |citeseerx=10.1.1.131.1338 |s2cid=10833328 }}</ref> 1965 में, एडवर्ड डब्ल्यू फोर्गी ने अनिवार्य रूप से विधि प्रकाशित की, यही कारण है कि इसे कभी-कभी लॉयड-फोर्गी एल्गोरिथम कहा जाता है।<ref name="forgy652">{{Cite journal |first=Edward W. |last=Forgy |year=1965 |title=Cluster analysis of multivariate data: efficiency versus interpretability of classifications |journal=Biometrics |volume=21 |issue=3 |pages=768–769 |jstor=2528559 }}</ref> | k-माध्यिका शब्द का प्रथम बार उपयोग जेम्स मैकक्वीन ने 1967 में किया था।<ref name="macqueen19672">{{cite conference |last=MacQueen |first=J. B. |year=1967 |title=बहुभिन्नरूपी टिप्पणियों के वर्गीकरण और विश्लेषण के लिए कुछ विधिया होती है। |url=http://projecteuclid.org/euclid.bsmsp/1200512992 |conference=Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability |publisher=University of California Press |volume=1 |pages=281–297 |mr=0214227 |zbl=0214.46201 |access-date=2009-04-07 }}</ref> चूँकि यह विचार 1956 में [[ह्यूगो स्टीनहॉस]] के पास वापस चला गया।<ref>{{cite journal |last=Steinhaus |first=Hugo |author-link=Hugo Steinhaus |year=1957 |title=Sur la division des corps matériels en parties |journal=Bull. Acad. Polon. Sci. |language=fr |volume=4 |issue=12 |pages=801–804 |mr=0090073 |zbl=0079.16403 }}</ref> मानक एल्गोरिथम प्रथम बार 1957 में [[बेल लैब्स]] के स्टुअर्ट लॉयड द्वारा [[ पल्स कोड मॉडुलेशन | पल्स कोड मॉडुलेशन]] के लिए प्रविधियों के रूप में प्रस्तावित किया गया था, चूँकि इसे 1982 तक जर्नल लेख के रूप में प्रकाशित नहीं किया गया था।<ref name="lloyd19572">{{cite journal |last=Lloyd |first=Stuart P. |year=1957 |title=पीसीएम में अल्प से अल्प वर्ग परिमाणीकरण होते है|journal=Bell Telephone Laboratories Paper }} Published in journal much later: {{cite journal |last=Lloyd |first=Stuart P. |year=1982 |title=Least squares quantization in PCM |url=http://www.cs.toronto.edu/~roweis/csc2515-2006/readings/lloyd57.pdf |journal=[[IEEE Transactions on Information Theory]] |volume=28 |issue=2 |pages=129–137 |doi=10.1109/TIT.1982.1056489 |access-date=2009-04-15 |citeseerx=10.1.1.131.1338 |s2cid=10833328 }}</ref> 1965 में, एडवर्ड डब्ल्यू फोर्गी ने अनिवार्य रूप से विधि प्रकाशित की, यही कारण है कि इसे कभी-कभी लॉयड-फोर्गी एल्गोरिथम कहा जाता है।<ref name="forgy652">{{Cite journal |first=Edward W. |last=Forgy |year=1965 |title=Cluster analysis of multivariate data: efficiency versus interpretability of classifications |journal=Biometrics |volume=21 |issue=3 |pages=768–769 |jstor=2528559 }}</ref> | ||
| Line 20: | Line 39: | ||
== एल्गोरिदम == | == एल्गोरिदम == | ||
=== मानक एल्गोरिदम (बेवकूफ के-साधन) === | === मानक एल्गोरिदम (बेवकूफ के-साधन) === | ||
<gallery class="center" widths="150px" caption="Demonstration of the standard algorithm"> | सबसे सरल एल्गोरिथ्म पुनरावृत्त शोधन प्रविधि का उपयोग करता है। इसकी सर्वव्यापकता के कारण, इसे प्रायः k-अर्थात एल्गोरिथम कहा जाता हैI इसे विशेष रूप से कंप्यूटर विज्ञान समुदाय में लॉयड्स एल्गोरिथम के रूप में भी जाना जाता है। इसे कभी-कभी नैवे के-साधन के रूप में भी जाना जाता है I | ||
कार्यभार चरण: प्रत्येक अवलोकन के समूह को निकटतम माध्य के साथ प्रस्तुत करता है। अल्प से अल्प वर्ग यूक्लिडियन दूरी के साथ।[7] (गणितीय रूप से, इसका अर्थ है साधनों द्वारा उत्पन्न वोरोनोई आरेख के अनुसार अवलोकनों को विभाजित करना।) | |||
जहां प्रत्येक ठीक को प्रदान किया गया है , भले ही यह उनमें से दो या अधिक को सौंपा जा सकता है। | |||
अद्यतन चरण: प्रत्येक समूह को अभिहस्तांकित किए गए अवलोकनों के लिए पुनर्गणना का अर्थ (केन्द्रक) होता है। | |||
एल्गोरिथम अभिसरण तब होता है जब कार्यभार अब परिवर्तित नहीं होते हैं। इष्टतम का शोध करने के लिए एल्गोरिदम उत्तरदायी नहीं है।[8] एल्गोरिथम को प्रायः दूरी के आधार पर निकटतम समूह में वस्तु अभिहस्तांकित करने के रूप में प्रस्तुत किया जाता है। (स्क्वायर) यूक्लिडियन दूरी के अतिरिक्त किसी भिन्न दूरी फ़ंक्शन का उपयोग करने से एल्गोरिथम को अभिसरण से बाधित किया जा सकता है। K-माध्यिका के विभिन्न संशोधन जैसे गोलाकार K-माध्यिका और K-मेडोइड्स को अन्य दूरी उपायों का उपयोग करने की अनुमति देने के लिए प्रस्तावित किया गया है। | |||
=== आरंभीकरण की विधि === | |||
सामान्यतः उपयोग की जाने वाली आरंभीकरण विधियाँ और अनियमित विभाजन हैं। Forgy विधि यादृच्छिक रूप से डेटा समुच्चय से k अवलोकन का चयन करती है और प्रारंभिक साधनों के रूप में इनका उपयोग करती है। यादृच्छिक विभाजन विधि के पूर्व उचित रूप से प्रत्येक अवलोकन के लिए माध्यम प्रदान करती है और फिर अद्यतन चरण पर आगे बढ़ती है, इस प्रकार प्रारंभिक माध्य की गणना माध्यम के यादृच्छिक रूप से अभिहस्तांकित किए गए बिंदुओं के केन्द्रक के रूप में की जाती है। फोर्जी विधि प्रारंभिक साधनों को फैलाने की प्रवृत्ति रखती है, जबकि यादृच्छिक विभाजन उन सभी को डेटा समुच्चय के केंद्र के निकट रखता है। हैमरली एट अल के अनुसार, यादृच्छिक विभाजन विधि सामान्यतः एल्गोरिदम जैसे k-हार्मोनिक साधनों और k-साधनों के लिए उत्तम होती है। अपेक्षा अधिकतमकरण और मानक के-साधन एल्गोरिदम के लिए, प्रारंभिकरण की फोर्जी विधि उत्तम है। सेलेबी एट अल द्वारा व्यापक अध्ययन होता है। चूँकि, पाया गया कि फोर्जी, अनियमित विभाजन और मैक्सिमिन जैसे लोकप्रिय आरंभीकरण विधि प्रायः निकृष्ट प्रदर्शन करते हैं, जबकि ब्रैडली और फ़य्यद का दृष्टिकोण सर्वश्रेष्ठ माध्यम में निरंतर प्रदर्शन करता है और K-means++|k-means++ सामान्यतः उचित प्रदर्शन करता है। | |||
[[File:K-means_convergence.gif|right|thumb|k-साधनों का अभिसरण]]<sup><sup><gallery class="center" widths="150px" caption="Demonstration of the standard algorithm"> | |||
File:K Means Example Step 1.svg|1. k प्रारंभिक साधन (इस स्थिति में k = 3) डेटा डोमेन (रंग में दिखाया गया) के अंदर यादृच्छिक रूप से उत्पन्न होते हैं। | File:K Means Example Step 1.svg|1. k प्रारंभिक साधन (इस स्थिति में k = 3) डेटा डोमेन (रंग में दिखाया गया) के अंदर यादृच्छिक रूप से उत्पन्न होते हैं। | ||
File:K Means Example Step 2.svg|2. k समूह प्रत्येक अवलोकन को निकटतम माध्य से जोड़कर बनाया जाता है। यहां के विभाजन माध्यम से उत्पन्न वोरोनोई आरेख का प्रतिनिधित्व करते हैं। | File:K Means Example Step 2.svg|2. k समूह प्रत्येक अवलोकन को निकटतम माध्य से जोड़कर बनाया जाता है। यहां के विभाजन माध्यम से उत्पन्न वोरोनोई आरेख का प्रतिनिधित्व करते हैं। | ||
File:K Means Example Step 3.svg|3. प्रत्येक k समूह का केन्द्रक नया माध्य बन जाता है। | File:K Means Example Step 3.svg|3. प्रत्येक k समूह का केन्द्रक नया माध्य बन जाता है। | ||
File:K Means Example Step 4.svg|4. अभिसरण होने तक चरण 2 और 3 दोहराए जाते हैं। | File:K Means Example Step 4.svg|4. अभिसरण होने तक चरण 2 और 3 दोहराए जाते हैं। | ||
</gallery> | </gallery><sup><sup>कार्यभार चरण को स्वीकृत अर्थ चरण कहा जाता है, जबकि अद्यतन चरण अधिकतमकरण चरण है, जो इस एल्गोरिथम को सामान्यीकृत स्वीकृत अर्थ-अधिकतमकरण एल्गोरिथम का रूपांतर बनाता है। | ||
<sup><sup> | |||
<sup><sup>कठिनाई | |||
<sup><sup> | |||
<sup><sup>डी आयामों में अवलोकन के लिए k-साधन समूह समस्या का इष्टतम समाधान का शोध करना है। | |||
<sup><sup> | |||
<sup><sup>दो समूहों के लिए भी सामान्य यूक्लिडियन अंतरिक्ष (डी आयामों में) में NP कठिन होते है। | |||
<sup><sup>NP-कठिन सामा<sup><sup><sup>[[Category:Articles with hatnote templates targeting a nonexistent page]]न्य संख्या में समूह के लिए विमान में भी, | |||
<sup><sup>यदि k और d (आयाम) निश्चित हैं, तो समस्या का समय से निवारण किया जा सकता है। | |||
<sup><sup>O(ndk+1) | |||
<sup><sup>, जहां n समूह होने वाली संस्थाओं की संख्या है। | |||
<sup><sup> | |||
<sup><sup>इस प्रकार, ऊपर दिए गए लॉयड के एल्गोरिथम जैसे विभिन्न अनुमानी एल्गोरिदम को सामान्यतः उपयोग किया जाता है। | |||
<sup><sup> | |||
<sup><sup>लॉयड्स एल्गोरिथम (और अधिकांश रूपांतर) का बढनेवाला समय है। | |||
<sup><sup>O(nkdi) | |||
<sup><sup>, जहाँ: | |||
<sup><sup> | |||
<sup><sup>n डी-रंगात्मक सदिश की संख्या है (क्लस्टर किया जाना है)। | |||
<sup><sup>कश्मीर समूहों की संख्या होती है। | |||
<sup><sup>I अभिसरण तक आवश्यक पुनरावृत्तियों की संख्या होती है। | |||
<sup><sup> | |||
<sup><sup>समूह संरचना वाले डेटा पर, अभिसरण तक पुनरावृत्तियों की संख्या प्रायः अल्प होती है, और परिणाम केवल पूर्व दर्जन पुनरावृत्तियों के पश्चात थोड़ा सुधार करते हैं। इसलिए लॉयड के एल्गोरिथ्म को व्यवहार में प्रायः रैखिक जटिलता वाला माना जाता है, चूँकि अभिसरण तक किए जाने पर यह निकृष्टतम-प्रकरण कठिनता अधिबहुपद में होता है। | |||
<sup><sup> | |||
<sup><sup>सबसे निकृष्ट स्थिति में, लॉयड के एल्गोरिथ्म की आवश्यकता होती है। | |||
<sup><sup>i=2Ω(n) | |||
<sup><sup> पुनरावृत्तियों, जिससे लॉयड के एल्गोरिथम की सबसे निकृष्ट स्थिति समय कठिन अधिबहुपद समय होता है।* लॉयड के K-माध्यिका एल्गोरिदम में बहुपद स्निग्ध बढनेवाला समय है। यह दिखाया गया है कि <रेफरी नाम = आर्थर, डेविड; मंथे, बी.; Roeglin, H. 20092 /> n बिंदुओं के इच्छानुकूल समुच्चय के लिए होता है। | |||
= | |||
<sup><sup>[0,1]d | |||
<sup><sup>, यदि प्रत्येक बिंदु माध्य के साथ सामान्य वितरण द्वारा स्वतंत्र रूप से चिंतित है 0 और विचरण | |||
<sup><sup>σ2 | |||
<sup><sup>, अपेक्षित चलने का समय k-अर्थात एल्गोरिद्म परिबद्ध है | |||
<sup><sup>O(n34k34d8log4(n)/σ6) | |||
<sup><sup>, जो बहुपद है। n, k, d और | |||
<sup><sup>1/σ | |||
<sup><sup>. | |||
<sup><sup>साधारण स्थितियों के लिए उत्तम सीमाएँ सिद्ध होती हैं। उदाहरण के लिए, यह दिखाया गया है कि k- साधन एल्गोरिथम का चलने का समय सीमाबद्ध है। | |||
<sup><sup>O(dn4M2) | |||
<sup><sup> के लिए n पूर्णांक जाली में अंक | |||
< | |||
के लिए | |||
<sup><sup>{1,…,M}d | |||
<sup><sup>. | |||
<sup><sup> | |||
<sup><sup> | |||
<sup><sup> | |||
<sup><sup> | |||
<sup><sup>रूपांतर | |||
<sup><sup>Jenks प्राकृतिक टूटता अनुकूलन: K-माध्यिका यूनीवेट डेटा पर प्रारम्भ होता है | |||
<sup><sup>K-माध्यिका समूह औसत के अतिरिक्त प्रत्येक आयाम में औसत का उपयोग करता है, और इस प्रकार अर्घ्य करता है | |||
<sup><sup>L1 | |||
<sup><sup> मानदंड (टैक्सीकैब ज्यामिति)। | |||
<sup><sup>K-माध्यिका (यह भी: माध्यिका के निकट विभाजन, पीएएम) माध्य के अतिरिक्त मेडॉइड का उपयोग करता है, और इस प्रकार इच्छानुकूल दूरी कार्यों के लिए दूरी का योग अल्प करता है। | |||
<sup><sup>फ़ज़ी समूह फ़ज़ी C-माध्यिका समूह K-माध्यिका का नरम वर्जन है, जहाँ प्रत्येक डेटा पॉइंट में प्रत्येक समूह से संबंधित फ़ज़ी श्रेणी होती है। | |||
<sup><sup>मिश्रण प्रारूप गॉसियन मिश्रण प्रारूप आश्वास-अधिकतमकरण एल्गोरिदम (ईएम एल्गोरिदम) के साथ प्रशिक्षित नियतात्मक कार्यभार के अतिरिक्त समूहों के लिए संभाव्य कार्यभार बनाए रखता है, और साधनों के अतिरिक्त बहुभिन्नरूपी गॉसियन वितरण करता है। | |||
<sup><sup>K-means++|k-means++ प्रारंभिक केंद्रों का इस प्रकार चयन करता है जो WCSS उद्देश्य पर सिद्ध ऊपरी सीमा देता है। | |||
<sup><sup>निस्पंदन एल्गोरिथ्म प्रत्येक k- साधन चरण को गति देने के लिए kd- ट्री का उपयोग करता है। | |||
<sup><sup>कुछ विधियाँ त्रिभुज असमानता का उपयोग करके प्रत्येक k- साधन चरण को गति देने का प्रयास करती हैं।* समूहों के मध्य बिंदुओं का आदान-प्रदान करके स्थानीय से संरक्षण करते है।* गोलाकार k- साधन क्लस्टरिंग एल्गोरिथ्म शाब्दिक डेटा के लिए उपयुक्त है। | |||
<sup><sup>पदानुक्रमित संस्करण जैसे द्विभाजित k- साधन, X-अर्थात समूह और G-अर्थात समूह पदानुक्रमित समूह, विभाजक समूह, और डेटा उपसमुच्चय में समूह की इष्टतम संख्या को स्वचालित रूप से निर्धारित करने का प्रयास भी कर सकता है। | |||
<sup><sup>समूह विश्लेषण आंतरिक मूल्यांकन उपाय जैसे सिल्हूट (समूह) डेटा उपसमुच्चय में समूह की संख्या निर्धारित करने में सहायक हो सकते हैं। | |||
<sup><sup>Minkowski भारित k-माध्यिका स्वचालित रूप से समूह विशिष्ट वैशिष्टय वेट की गणना करता है, सहज विचार का समर्थन करता है कि विशेषता में भिन्न-भिन्न सुविधाओं पर प्रासंगिकता की भिन्न-भिन्न उपाधि हो सकती है। इन भारों का उपयोग किसी दिए गए डेटा समुच्चय को स्तर करने के लिए भी किया जा सकता है, जिससे समूह की अपेक्षित संख्या में समूह वैधता सूचकांक को अनुकूलित करने की संभावना बढ़ जाती है। | |||
<sup><sup>अल्प-दल k- साधन डेटा उपसमुच्चय के लिए अल्प दल प्रतिमान का उपयोग करके भिन्नता जो मेमोरी में योग्य नहीं होती है। | |||
<sup><sup>ओत्सु की विधि | |||
<sup><sup>हार्टिगन-वोंग विधि | |||
<sup><sup> | |||
<sup><sup>हार्टिगन और वोंग की विधिK-माध्यिका एल्गोरिदम की विविधता प्रदान करता है जो विभिन्न समाधान अद्यतनों के साथ न्यूनतम योग-वर्ग समस्या के स्थानीय न्यूनतम की ओर बढ़ता है। विधि स्थानीय खोज (अनुकूलन) है, जो मानक को भिन्न समूह में स्थानांतरित करने का प्रयत्न करती है जब तक कि यह प्रक्रिया उद्देश्य फंक्शन में सुधार करती है। जब उद्देश्य में सुधार के साथ किसी भिन्न समूह में कोई प्रतिमान स्थानांतरित नहीं किया जा सकता है, तो विधि समाप्त हो जाती है (स्थानीय न्यूनतम में)। शास्त्रीय के-साधन के समान ही, दृष्टिकोण अनुमानी बना हुआ है, क्योंकि यह आवश्यक रूप से आश्वासन नहीं देता है कि अंतिम समाधान विश्व स्तर पर इष्टतम है। | |||
<sup><sup> | |||
<sup><sup>होने देना | |||
<sup><sup>φ(Sj) | |||
<sup><sup> की व्यक्तिगत वित्त हो | |||
<sup><sup>Sj | |||
<sup><sup> द्वारा परिभाषित | |||
<sup><sup>∑x∈Sj(x−μj)2 | |||
<sup><sup>, साथ | |||
<sup><sup>μj | |||
<sup><sup> समूह का केंद्र होता है। | |||
<sup><sup> | |||
<sup><sup>कार्यभार विधि: हार्टिगन और वोंग की विधि बिंदुओं को यादृच्छिक समूहों में विभाजित करके प्रारम्भ होती है | |||
<sup><sup>{Sj}j∈{1,⋯k} | |||
<sup><sup>। | |||
<sup><sup> | |||
<sup><sup>अद्यतन चरण: आगामी यह निर्धारित करता है | |||
<sup><sup>n,m∈{1,…,k} | |||
<sup><sup> और | |||
<sup><sup>x∈Sn | |||
<sup><sup> जिसके लिए निम्नलिखित कार्य अधिकतम तक पहुँचता है। | |||
<sup><sup> | |||
<sup><sup>Δ(m,n,x)=φ(Sn)+φ(Sm)−φ(Sn∖{x})−φ(Sm∪{x}) | |||
<sup><sup> | |||
<sup><sup>के लिए | |||
<sup><sup>x,n,m | |||
<sup><sup> जो इस अधिकतम तक पहुँचे, | |||
<sup><sup>x | |||
<sup><sup> समूहों से चलता है | |||
<sup><sup>Sn | |||
<sup><sup> समूह को | |||
<sup><sup>Sm | |||
<sup><sup>निर्धारित करता है। | |||
<sup><sup> | |||
<sup><sup>समाप्ति: एल्गोरिथम टर्मिनेट होता है | |||
<sup><sup>Δ(m,n,x) | |||
<sup><sup> सभी के लिए शून्य से अर्घ्य है | |||
<sup><sup>x,n,m | |||
<sup><sup>. | |||
<sup><sup> | |||
<sup><sup>विभिन्न चाल स्वीकृति रणनीतियों का उपयोग किया जा सकता है। पूर्व-सुधार की रणनीति में, किसी भी सुधार के स्थानांतरण को प्रारम्भ किया जा सकता है, जबकि सर्वोत्तम-सुधार की रणनीति में, सभी संभव स्थानांतरणों का पुनरावृत्त रूप से परीक्षण किया जाता है और प्रत्येक पुनरावृत्ति पर केवल सर्वश्रेष्ठ को प्रारम्भ किया जाता है। पूर्व दृष्टिकोण गति का समर्थन करता है, दृष्टिकोण सामान्यतः अतिरिक्त कम्प्यूटेशनल समय के मूल्य पर समाधान की गुणवत्ता का पक्ष लेता है। कार्यक्रम | |||
<sup><sup>Δ | |||
<sup><sup> स्थानांतरण के परिणाम की गणना करने के लिए उपयोग किया जाता है, समानता का उपयोग करके भी कुशलतापूर्वक मूल्यांकन किया जा सकता है। | |||
<sup><sup> | |||
<sup><sup>Δ(x,n,m)=∣Sn∣∣Sn∣−1⋅‖μn−x‖2−∣Sm∣∣Sm∣+1⋅‖μm−x‖2. | |||
<sup><sup> | |||
<sup><sup> | |||
<sup><sup> | |||
<sup><sup> | |||
<sup><sup>वैश्विक अनुकूलन और मेटाह्यूरिस्टिक्स | |||
<sup><sup> | |||
शास्त्रीय k- साधन एल्गोरिथ्म एवं इसकी विविधताओं को "केंद्र"> के रूप में परिभाषित न्यूनतम-योग-वर्ग समूह समस्या के केवल स्थानीय न्यूनतम में परिवर्तित करने के लिए जाना जाता है। <math> \underset{\mathbf{S}} {\operatorname{arg\,min}} \sum_{i=1}^{k} \sum_{\mathbf x \in S_i} \left\| \mathbf x - \boldsymbol\mu_i \right\|^2 .</math>कई अध्ययनों ने एल्गोरिथम के अभिसरण व्यवहार में सुधार करने एवं वैश्विक इष्टतम (या अल्प से अल्प, उत्तम गुणवत्ता के स्थानीय न्यूनतम) प्राप्त करने की संभावना को अधिकतम करने का प्रयत्न किया है। पूर्व अनुभागों में वर्णन किया गया था। आरंभीकरण एवं पुनः आरंभ करने की प्रविधि उत्तम समाधान का शोध करने के लिए विकल्प हैं। [[ शाखा और बंधन | शाखा एवं बंधन]] एवं [[अर्ध निश्चित प्रोग्रामिंग]] पर आधारित वैश्विक अनुकूलन एल्गोरिदम ने 4,177 संस्थाओं एवं 20,531 सुविधाओं के साथ डेटासमुच्चय के लिए ''सिद्ध रूप से इष्टतम'' समाधान प्रस्तुत किए हैं।<ref>{{Cite journal |last1=Piccialli |first1=Veronica |last2=Sudoso |first2=Antonio M. |last3=Wiegele |first3=Angelika |date=2022-03-28 |title=SOS-SDP: An Exact Solver for Minimum Sum-of-Squares Clustering |url=http://pubsonline.informs.org/doi/10.1287/ijoc.2022.1166 |journal=INFORMS Journal on Computing |volume=34 |issue=4 |language=en |pages=2144–2162 |doi=10.1287/ijoc.2022.1166 |arxiv=2104.11542 |s2cid=233388043 |issn=1091-9856}}</ref> जैसा कि अपेक्षित था, उपजात अनुकूलन समस्या की NP-कठोरता के कारण, K-साधनों के लिए इष्टतम एल्गोरिदम का कम्प्यूटेशनल समय इस आकार से तीव्र गति से बढ़ता है। अन्य अनुमानों की गुणवत्ता का मूल्यांकन करने के लिए, अल्प एवं मध्यम स्तर के लिए इष्टतम समाधान अभी भी बेंचमार्क उपकरण के रूप में मूल्यवान हैं। नियंत्रित कम्प्यूटेशनल समय के अंदर उच्च-गुणवत्ता वाले स्थानीय मिनिमा का शोध करने के लिए, किन्तु इष्टतमता का कथन के बिना, अन्य कार्यों ने [[मेटाह्यूरिस्टिक्स]] एवं अन्य [[वैश्विक अनुकूलन]] प्रविधियों की जानकारी ज्ञात की है। उदाहरण के लिए, वृद्धिशील दृष्टिकोण एवं उत्तल अनुकूलन के आधार पर,<ref name="bagirov16">{{Cite journal|last1= Bagirov |first1=A. M. |last2=Taheri |first2=S. |last3=Ugon|first3=J.|year=2016 |title= न्यूनतम सम-वर्ग समूह समस्याओं के लिए गैर-अरूक्ष डीसी प्रोग्रामिंग दृष्टिकोण|journal= Pattern Recognition |volume=53 |pages=12–24 |doi= 10.1016/j.patcog.2015.11.011|bibcode=2016PatRe..53...12B }}</ref> यादृच्छिक आदान-प्रदान<ref name="franti18">{{Cite journal |last1= Fränti |first1=Pasi |year=2018 |title= यादृच्छिक स्वैप क्लस्टरिंग की दक्षता|journal= Journal of Big Data |volume=5 |issue=1|pages=1–21 |doi= 10.1186/s40537-018-0122-y|doi-access=free }}</ref> (अर्थात, [[पुनरावृत्त स्थानीय शोध]]), परिवर्तनशील परस्पर शोध<ref>{{Cite journal |last1= Hansen |first1=P. |last2=Mladenovic |first2=N. |year=2001 |title= J-Means: A new local search heuristic for minimum sum of squares clustering|journal=Pattern Recognition |volume=34 |issue=2|pages=405–413 |doi= 10.1016/S0031-3203(99)00216-2|bibcode=2001PatRe..34..405H }}</ref> एवं [[आनुवंशिक एल्गोरिदम]]।<ref>{{Cite journal |last1= Krishna |first1=K. |last2=Murty |first2=M. N. |year=1999 |title= आनुवंशिक K-अर्थात एल्गोरिथम होते है।journal= IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics |volume=29 |issue=3|pages=433–439 |doi= 10.1109/3477.764879|pmid=18252317 |url=https://www.researchgate.net/publication/5600582}}</ref><ref name="gribel19">{{Cite journal |last1= Gribel |first1=Daniel | last2=Vidal |first2=Thibaut| year=2019 |title= HG-means: A scalable hybrid metaheuristic for minimum sum-of-squares clustering |journal=Pattern Recognition |volume=88 |pages=569–583 |doi= 10.1016/j.patcog.2018.12.022|arxiv=1804.09813 |s2cid=13746584 }}</ref> यह वास्तव में ज्ञात है कि न्यूनतम सम-वर्ग माध्यमिंक समस्या का उत्तम स्थानीय न्यूनतम का शोध करने से उच्च आयाम वाले वैशिष्टय अंतर में माध्यम संरचनाओं को पुनर्प्राप्त करने में विफलता एवं सफलता के मध्य अंतर हो सकता है। | |||
== उल्लेख == | == उल्लेख == | ||
होते ह[[File:Iris_Flowers_Clustering_kMeans.svg|thumb|450x450px|K-माध्यिका [[आइरिस पूर्ण डेटा उपसमुच्चय]] के लिए समूह परिणाम और [[सूचकांक-संरचनाओं द्वारा समर्थित केडीडी-अनुप्रयोगों के विकास के लिए पर्यावरण]] का उपयोग करके वास्तविक प्रजातियों की कल्पना की गई। समूह साधनों को बड़े, अर्ध-पारदर्शी प्रतीकों का उपयोग करके चिह्नित किया जाता है।]]<sup><sup><sup>[[File:ClusterAnalysis_Mouse.svg|thumb|450x450px|k-अर्थ समूह के प्रति कृत्रिम डेटाउ उपसमुच्चय (माउस) पर [[ईएम समूह]] समान आकार के समूहों का उत्पादन करने के लिए K-साधन की प्रवृत्ति यहां निकृष्ट परिणामों की ओर ले जाती है, जबकि ईएम डेटा उपसमुच्चय में उपस्थित विभिन्न त्रिज्या वाले गॉसियन वितरण से लाभान्वित होता है।]]K-माध्यिका की तीन प्रमुख विशेषताएं जो इसे कुशल बनाती हैं, प्रायः इसकी सबसे बड़ी अल्पियां मानी जाती हैं। | |||
[[File:Iris_Flowers_Clustering_kMeans.svg|thumb|450x450px|K-माध्यिका [[आइरिस पूर्ण डेटा उपसमुच्चय]] के लिए समूह परिणाम और [[सूचकांक-संरचनाओं द्वारा समर्थित केडीडी-अनुप्रयोगों के विकास के लिए पर्यावरण]] का उपयोग करके वास्तविक प्रजातियों की कल्पना की गई। समूह साधनों को बड़े, अर्ध-पारदर्शी प्रतीकों का उपयोग करके चिह्नित किया जाता है।]] | |||
[[File:ClusterAnalysis_Mouse.svg|thumb|450x450px|k-अर्थ समूह के प्रति कृत्रिम डेटाउ उपसमुच्चय (माउस) पर [[ईएम समूह]] समान आकार के समूहों का उत्पादन करने के लिए K-साधन की प्रवृत्ति यहां निकृष्ट परिणामों की ओर ले जाती है, जबकि ईएम डेटा उपसमुच्चय में उपस्थित विभिन्न त्रिज्या वाले गॉसियन वितरण से लाभान्वित होता है।]]K-माध्यिका की तीन प्रमुख विशेषताएं जो इसे कुशल बनाती हैं, प्रायः इसकी सबसे बड़ी अल्पियां मानी जाती हैं। | |||
* यूक्लिडियन दूरी का उपयोग [[मीट्रिक (गणित)]] के रूप में किया जाता है और विचरण का उपयोग समूह स्कैटर के माप के रूप में किया जाता है। | * यूक्लिडियन दूरी का उपयोग [[मीट्रिक (गणित)]] के रूप में किया जाता है और विचरण का उपयोग समूह स्कैटर के माप के रूप में किया जाता है। | ||
* समूह k की संख्या इनपुट पैरामीटर है। k का अनुचित विकल्प निकृष्ट परिणाम दे सकता है। इसीलिए, k-माध्यिका करते समय, डेटा उपसमुच्चय में समूह की संख्या निर्धारित करने के लिए नैदानिक चेक चलाना महत्वपूर्ण है। | * समूह k की संख्या इनपुट पैरामीटर है। k का अनुचित विकल्प निकृष्ट परिणाम दे सकता है। इसीलिए, k-माध्यिका करते समय, डेटा उपसमुच्चय में समूह की संख्या निर्धारित करने के लिए नैदानिक चेक चलाना महत्वपूर्ण है। | ||
* स्थानीय न्यूनतम के अभिसरण से विपरीत (गलत) परिणाम उत्पन्न हो सकते हैं (चित्र में उदाहरण देखें)। | * स्थानीय न्यूनतम के अभिसरण से विपरीत (गलत) परिणाम उत्पन्न हो सकते हैं (चित्र में उदाहरण देखें)। | ||
K- साधन की प्रमुख सीमा इसका समूह प्रारूप है। अवधारणा गोलाकार समूहों पर आधारित है जो वियोज्य हैं जिससे माध्य समूह केंद्र की ओर अभिसरण होता है। समूह समान आकार के होने की अपेक्षा है, जिससे निकटतम समूह केंद्र का कार्यभार सही हो। उदाहरण के लिए जब k- साधन को मान के साथ प्रारम्भ किया जाता है। <math>k=3</math> प्रसिद्ध आइरिस फूल डेटा उपसमुच्चय पर, परिणाम प्रायः डेटा उपसमुच्चय में निहित तीन आइरिस (पौधे) प्रजातियों को भिन्न करने में विफल रहता है। साथ <math>k=2</math>, दो दृश्य समूहों (दो प्रजातियों वाला ) का शोध किया जायेगा, जबकि साथ में <math>k=3</math> दो समूहों को दो समान भागों में विभाजित किया जाएगा। वास्तव में, <math>k=2</math> डेटा उपसमुच्चय में 3 वर्ग होने के पश्चात, इस डेटा उपसमुच्चय के लिए अधिक उपयुक्त है। किसी भी अन्य समूह एल्गोरिदम के साथ, K-साधन परिणाम यह मानते हैं कि डेटा कुछ मानदंडों को पूर्ण करता है। यह कुछ डेटा उपसमुच्चय पर उचित कार्य करता है और दूसरों पर विफल रहता है। | K- साधन की प्रमुख सीमा इसका समूह प्रारूप है। अवधारणा गोलाकार समूहों पर आधारित है जो वियोज्य हैं जिससे माध्य समूह केंद्र की ओर अभिसरण होता है। समूह समान आकार के होने की अपेक्षा है, जिससे निकटतम समूह केंद्र का कार्यभार सही हो। उदाहरण के लिए जब k- साधन को मान के साथ प्रारम्भ किया जाता है। <math>k=3</math> प्रसिद्ध आइरिस फूल डेटा उपसमुच्चय पर, परिणाम प्रायः डेटा उपसमुच्चय में निहित तीन आइरिस (पौधे) प्रजातियों को भिन्न करने में विफल रहता है। साथ <math>k=2</math>, दो दृश्य समूहों (दो प्रजातियों वाला ) का शोध किया जायेगा, जबकि साथ में <math>k=3</math> दो समूहों को दो समान भागों में विभाजित किया जाएगा। वास्तव में, <math>k=2</math> डेटा उपसमुच्चय में 3 वर्ग होने के पश्चात, इस डेटा उपसमुच्चय के लिए अधिक उपयुक्त है। किसी भी अन्य समूह एल्गोरिदम के साथ, K-साधन परिणाम यह मानते हैं कि डेटा कुछ मानदंडों को पूर्ण करता है। यह कुछ डेटा उपसमुच्चय पर उचित कार्य करता है और दूसरों पर विफल रहता है। | ||
| Line 114: | Line 301: | ||
== अनुप्रयोग == | == अनुप्रयोग == | ||
k-माध्यिका समूह अपेक्षाकृत बड़े डेटा उपसमुच्चय पर प्रारम्भ करना सरल है, विशेष रूप से जब ह्यूरिस्टिक्स जैसे कि लॉयड्स एल्गोरिथम का उपयोग करते हैं। इसे कई अन्य डोमेन के मध्य [[व्यापार विभाजन]], [[कंप्यूटर दृष्टि]] और [[खगोल]] विज्ञान में सफलतापूर्वक उपयोग किया गया है। यह प्रायः अन्य एल्गोरिदम के लिए प्रसंस्करण चरण के रूप में उपयोग किया जाता है, उदाहरण के लिए प्रारंभिक व्यवस्था के प्रारूप का शोध करने के लिए होता है। | k-माध्यिका समूह अपेक्षाकृत बड़े डेटा उपसमुच्चय पर प्रारम्भ करना सरल है, विशेष रूप से जब ह्यूरिस्टिक्स जैसे कि लॉयड्स एल्गोरिथम का उपयोग करते हैं। इसे कई अन्य डोमेन के मध्य [[व्यापार विभाजन]], [[कंप्यूटर दृष्टि]] और [[खगोल]] विज्ञान में सफलतापूर्वक उपयोग किया गया है। यह प्रायः अन्य एल्गोरिदम के लिए प्रसंस्करण चरण के रूप में उपयोग किया जाता है, उदाहरण के लिए प्रारंभिक व्यवस्था के प्रारूप का शोध करने के लिए होता है। | ||
=== सदिश परिमाणीकरण === | === सदिश परिमाणीकरण === | ||
{{Main|Vector quantization}} | {{Main|Vector quantization}} | ||
[[File:Rosa_Gold_Glow_2_small_noblue.png|right|frame|दो-प्रणाली (चित्रण उद्देश्यों के लिए - केवल लाल और हरे रंग के प्रणाली) रंगीन छवि]] | [[File:Rosa_Gold_Glow_2_small_noblue.png|right|frame|दो-प्रणाली (चित्रण उद्देश्यों के लिए - केवल लाल और हरे रंग के प्रणाली) रंगीन छवि]][[File:Rosa_Gold_Glow_2_small_noblue_color_space.png|right|thumb|250x250px|k-माध्यिका का उपयोग करके वोरोनोई कोशिकाओं में ऊपर की छवि में उपस्थित रंगों का सदिश परिमाणीकरण]]k-साधन एकल प्रसंस्करण से उत्पन्न होता है, एवं अभी भी इस डोमेन में उपयोग होता है। उदाहरण के लिए, [[कंप्यूटर चित्रलेख]] में, [[रंग परिमाणीकरण]] | ||
[[File:Rosa_Gold_Glow_2_small_noblue_color_space.png|right|thumb|250x250px|k-माध्यिका का उपयोग करके वोरोनोई कोशिकाओं में ऊपर की छवि में उपस्थित रंगों का सदिश परिमाणीकरण]]k-साधन एकल प्रसंस्करण से उत्पन्न होता है, एवं अभी भी इस डोमेन में उपयोग होता है। उदाहरण के लिए, [[कंप्यूटर चित्रलेख]] में, [[रंग परिमाणीकरण]] | |||
<sup><sup><sup>छ | |||
[[Category:CS1 English-language sources (en)]] | |||
<sup><sup><sup>व | |||
[[Category:CS1 errors]] | |||
<sup><sup><sup>ि | |||
[[Category:CS1 français-language sources (fr)]] | |||
[[Category:Lua-based templates]] | |||
<sup><sup><sup>क | |||
[[Category:Multi-column templates]] | |||
<sup><sup><sup>े | |||
[[Category:Pages using div col with small parameter]] | |||
[[Category:Pages with reference errors]] | |||
<sup><sup><sup>[[पैलेट (कंप्यूटिंग)|प]] | |||
[[Category:Pages with script errors]] | |||
<sup><sup><sup>[[पैलेट (कंप्यूटिंग)|ै]] | |||
[[Category:Short description with empty Wikidata description]] | |||
<sup><sup><sup>[[पैलेट (कंप्यूटिंग)|ल]] | |||
[[Category:Templates Vigyan Ready]] | |||
<sup><sup><sup>[[पैलेट (कंप्यूटिंग)|े]] | |||
[[Category:Templates that add a tracking category]] | |||
<sup><sup><sup>[[पैलेट (कंप्यूटिंग)|ट]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
<sup><sup><sup>[[पैलेट (कंप्यूटिंग)|(]] | |||
[[Category:Templates using under-protected Lua modules]] | |||
<sup><sup><sup>[[पैलेट (कंप्यूटिंग)|क]] | |||
[[Category:Wikipedia fully protected templates|Div col]] | |||
<sup><sup><sup>[[पैलेट (कंप्यूटिंग)|ंप्यूटिंग)]] रंगों की निश्चित संख्या में अल्प करने का कार्य है। इस कार्य के लिए k-माध्यि एल्गोरिदम का सरलता से उपयोग किया जा सकता है एवं प्रतिस्पर्धी परिणाम उत्पन्न करता है। इस दृष्टिकोण के लिए उपयोग का विषय [[छवि विभाजन]] है। सदिश परिमाणीकरण के अन्य उपयोगों में [[प्रतिरूपकरण (सांख्यिकी)]] | गैर-यादृच्छिक प्रतिरूपकरण सम्मिलित है, क्योंकि k-साधन का उपयोग आगे के विश्लेषण के लिए बड़े डेटा समुच्चय से k भिन्न किन्तु प्रोटोटाइपिक वस्तुओं का चयन करने के लिए सरलता से किया जा सकता है। | |||
=== समूह विश्लेषण === | === समूह विश्लेषण === | ||
{{Main|Cluster analysis}} | {{Main|Cluster analysis}}माध्यम विश्लेषण में, k- साधन एल्गोरिथ्म का उपयोग इनपुट डेटा समुच्चय को k विभाजन (माध्यम) में विभाजित करने के लिए किया जा सकता है। | ||
चूँकि, शुद्ध k-साधन एल्गोरिदम अधिक नमनीय नहीं है, और (कि जब ऊपर के रूप में सदिश अनुमान वास्तव में वांछित उपयोग विषय है)। विशेष रूप से, पैरामीटर k का चयन कठिन माना जाता है (जैसा कि ऊपर वर्णन किया गया है) जब बाहरी बाधाओं द्वारा नहीं दिया जाता है। इसका उपयोग इच्छानुकूल दूरी के कार्यों या गैर-संख्यात्मक डेटा के साथ नहीं किया जा सकता है। इन उपयोग विषयो के लिए, कई अन्य एल्गोरिदम श्रेष्ठ हैं। | चूँकि, शुद्ध k-साधन एल्गोरिदम अधिक नमनीय नहीं है, और (कि जब ऊपर के रूप में सदिश अनुमान वास्तव में वांछित उपयोग विषय है)। विशेष रूप से, पैरामीटर k का चयन कठिन माना जाता है (जैसा कि ऊपर वर्णन किया गया है) जब बाहरी बाधाओं द्वारा नहीं दिया जाता है। इसका उपयोग इच्छानुकूल दूरी के कार्यों या गैर-संख्यात्मक डेटा के साथ नहीं किया जा सकता है। इन उपयोग विषयो के लिए, कई अन्य एल्गोरिदम श्रेष्ठ हैं। | ||
=== [[विशेष अधिगम]] === | === [[विशेष अधिगम]] === | ||
k-means समूह का उपयोग विशेष अधिगम (या [[ शब्दकोश सीखना ]] ) विधि के रूप में किया गया है, या तो पर्यवेक्षित अधिगम या [[ अनियंत्रित शिक्षा ]] ।<ref name="Coates20122">{{cite book |year=2012 |chapter=Learning feature representations with ''k''-means |title=Neural Networks: Tricks of the Trade |publisher=Springer |chapter-url=https://cs.stanford.edu/~acoates/papers/coatesng_nntot2012.pdf |last2=Ng |first2=Andrew Y. |last1=Coates |first1=Adam |editor=Montavon, G. |editor2=Orr, G. B. |editor3=Müller, K.-R. |editor3-link=Klaus-Robert Müller}}</ref> मूल दृष्टिकोण सबसे प्रथम इनपुट प्रशिक्षण डेटा (जिसे लेबल करने की आवश्यकता नहीं है) का उपयोग करके k- साधन समूह प्रतिनिधित्व को प्रशिक्षित करना है। किसी भी इनपुट डेटा को नए विशेष स्थान में परियोजना करने के लिए, संकेतीकरण फ़ंक्शन, जैसे कि केन्द्रक स्थानों के साथ डेटम का थ्रेशोल्ड आव्यूह-उत्पाद, डेटम से प्रत्येक केन्द्रक तक की दूरी की गणना करता है, या बस निकटतम के लिए संकेतक फ़ंक्शन केन्द्रक,<ref name="Coates20122" /><ref>{{cite conference |last1=Csurka |first1=Gabriella |last2=Dance |first2=Christopher C. |last3=Fan |first3=Lixin |last4=Willamowski |first4=Jutta |last5=Bray |first5=Cédric |year=2004 |title=मुख्य बिंदुओं के बैग के साथ दृश्य वर्गीकरण|url=https://www.cs.cmu.edu/~efros/courses/LBMV07/Papers/csurka-eccv-04.pdf |conference=ECCV Workshop on Statistical Learning in Computer Vision }}</ref> या दूरी का कुछ सहज परिवर्तन होता है।<ref name="coates20112">{{cite conference |last1=Coates |first1=Adam |last2=Lee |first2=Honglak |last3=Ng |first3=Andrew Y. |year=2011 |title=उपेक्षा विशेष अधिगम में एकल-स्तर नेटवर्क के विश्लेषण |url=http://www.stanford.edu/~acoates/papers/coatesleeng_aistats_2011.pdf |url-status=dead |conference=International Conference on Artificial Intelligence and Statistics (AISTATS) |archive-url=https://web.archive.org/web/20130510120705/http://www.stanford.edu/~acoates/papers/coatesleeng_aistats_2011.pdf |archive-date=2013-05-10 }}</ref> वैकल्पिक रूप से, रेडियल आधार फ़ंक्शन के माध्यम से प्रतिमान-समूह दूरी को परिवर्तित करने से [[दीप्तिमान आधार फंक्शन नेटवर्क]] की छिपी हुई परत प्राप्त होती है।<ref name="schwenker2">{{cite journal |last1=Schwenker |first1=Friedhelm |last2=Kestler |first2=Hans A. |last3=Palm |first3=Günther |year=2001 |title=दीप्तिमान-आधार-फंक्शन नेटवर्क के लिए सीखने के तीन चरण|journal=Neural Networks |volume=14 |issue=4–5 |pages=439–458 |citeseerx=10.1.1.109.312 |doi=10.1016/s0893-6080(01)00027-2 |pmid=11411631 }}</ref> | k-means समूह का उपयोग विशेष अधिगम (या [[ शब्दकोश सीखना]] ) विधि के रूप में किया गया है, या तो पर्यवेक्षित अधिगम या [[ अनियंत्रित शिक्षा]] ।<ref name="Coates20122">{{cite book |year=2012 |chapter=Learning feature representations with ''k''-means |title=Neural Networks: Tricks of the Trade |publisher=Springer |chapter-url=https://cs.stanford.edu/~acoates/papers/coatesng_nntot2012.pdf |last2=Ng |first2=Andrew Y. |last1=Coates |first1=Adam |editor=Montavon, G. |editor2=Orr, G. B. |editor3=Müller, K.-R. |editor3-link=Klaus-Robert Müller}}</ref> मूल दृष्टिकोण सबसे प्रथम इनपुट प्रशिक्षण डेटा (जिसे लेबल करने की आवश्यकता नहीं है) का उपयोग करके k- साधन समूह प्रतिनिधित्व को प्रशिक्षित करना है। किसी भी इनपुट डेटा को नए विशेष स्थान में परियोजना करने के लिए, संकेतीकरण फ़ंक्शन, जैसे कि केन्द्रक स्थानों के साथ डेटम का थ्रेशोल्ड आव्यूह-उत्पाद, डेटम से प्रत्येक केन्द्रक तक की दूरी की गणना करता है, या बस निकटतम के लिए संकेतक फ़ंक्शन केन्द्रक,<ref name="Coates20122" /><ref>{{cite conference |last1=Csurka |first1=Gabriella |last2=Dance |first2=Christopher C. |last3=Fan |first3=Lixin |last4=Willamowski |first4=Jutta |last5=Bray |first5=Cédric |year=2004 |title=मुख्य बिंदुओं के बैग के साथ दृश्य वर्गीकरण|url=https://www.cs.cmu.edu/~efros/courses/LBMV07/Papers/csurka-eccv-04.pdf |conference=ECCV Workshop on Statistical Learning in Computer Vision }}</ref> या दूरी का कुछ सहज परिवर्तन होता है।<ref name="coates20112">{{cite conference |last1=Coates |first1=Adam |last2=Lee |first2=Honglak |last3=Ng |first3=Andrew Y. |year=2011 |title=उपेक्षा विशेष अधिगम में एकल-स्तर नेटवर्क के विश्लेषण |url=http://www.stanford.edu/~acoates/papers/coatesleeng_aistats_2011.pdf |url-status=dead |conference=International Conference on Artificial Intelligence and Statistics (AISTATS) |archive-url=https://web.archive.org/web/20130510120705/http://www.stanford.edu/~acoates/papers/coatesleeng_aistats_2011.pdf |archive-date=2013-05-10 }}</ref> वैकल्पिक रूप से, रेडियल आधार फ़ंक्शन के माध्यम से प्रतिमान-समूह दूरी को परिवर्तित करने से [[दीप्तिमान आधार फंक्शन नेटवर्क]] की छिपी हुई परत प्राप्त होती है।<ref name="schwenker2">{{cite journal |last1=Schwenker |first1=Friedhelm |last2=Kestler |first2=Hans A. |last3=Palm |first3=Günther |year=2001 |title=दीप्तिमान-आधार-फंक्शन नेटवर्क के लिए सीखने के तीन चरण|journal=Neural Networks |volume=14 |issue=4–5 |pages=439–458 |citeseerx=10.1.1.109.312 |doi=10.1016/s0893-6080(01)00027-2 |pmid=11411631 }}</ref> | ||
[[प्राकृतिक भाषा प्रसंस्करण]] (विशेष रूप से नामित इकाई पहचान के लिए) में अर्ध-पर्यवेक्षित सीखने के लिए K-साधनों के इस उपयोग को सरल, रैखिक वर्गीकरण के साथ सफलतापूर्वक जोड़ा गया है।<ref>{{cite conference |last1=Lin |first1=Dekang |last2=Wu |first2=Xiaoyun |year=2009 |title=भेदभावपूर्ण सीखने के लिए वाक्यांश समूह|url=http://www.aclweb.org/anthology/P/P09/P09-1116.pdf |conference=Annual Meeting of the [[Association for Computational Linguistics|ACL]] and IJCNLP |pages=1030–1038 }}</ref> और कंप्यूटर दृष्टि में वस्तु रिकग्निशन मानक पर, [[ऑटोएनकोडर]] और [प्रतिबंधित विद्युत मशीन] जैसे अधिक परिष्कृत विशेष अधिगम दृष्टिकोण के साथ तुलनात्मक प्रदर्शन प्रदर्शित करने के लिए पाया गया।<ref name="coates20112" />चूँकि, समान प्रदर्शन के लिए इसे सामान्यतः अधिक डेटा की आवश्यकता होती है, क्योंकि प्रत्येक डेटा बिंदु केवल सुविधा में योगदान देता है।<ref name="Coates20122" /> | [[प्राकृतिक भाषा प्रसंस्करण]] (विशेष रूप से नामित इकाई पहचान के लिए) में अर्ध-पर्यवेक्षित सीखने के लिए K-साधनों के इस उपयोग को सरल, रैखिक वर्गीकरण के साथ सफलतापूर्वक जोड़ा गया है।<ref>{{cite conference |last1=Lin |first1=Dekang |last2=Wu |first2=Xiaoyun |year=2009 |title=भेदभावपूर्ण सीखने के लिए वाक्यांश समूह|url=http://www.aclweb.org/anthology/P/P09/P09-1116.pdf |conference=Annual Meeting of the [[Association for Computational Linguistics|ACL]] and IJCNLP |pages=1030–1038 }}</ref> और कंप्यूटर दृष्टि में वस्तु रिकग्निशन मानक पर, [[ऑटोएनकोडर]] और [प्रतिबंधित विद्युत मशीन] जैसे अधिक परिष्कृत विशेष अधिगम दृष्टिकोण के साथ तुलनात्मक प्रदर्शन प्रदर्शित करने के लिए पाया गया।<ref name="coates20112" />चूँकि, समान प्रदर्शन के लिए इसे सामान्यतः अधिक डेटा की आवश्यकता होती है, क्योंकि प्रत्येक डेटा बिंदु केवल सुविधा में योगदान देता है।<ref name="Coates20122" /> | ||
== अन्य एल्गोरिदम से संबंध == | == अन्य एल्गोरिदम से संबंध == | ||
=== गॉसियन मिश्रण प्रारूप === | === गॉसियन मिश्रण प्रारूप === | ||
{{Main|Gaussian mixture model}} | {{Main|Gaussian mixture model}}K-माध्यिका माध्यम के लिए मंद मानक एल्गोरिथ्म, और इसके संबद्ध अपेक्षा-अधिकतमकरण एल्गोरिथ्म, गॉसियन मिश्रण प्रारूप का विशेष विषय है। विशेष रूप से, सीमित स्थिति जब सभी सहप्रसरणों को विकर्ण, समान और अपरिमेय होने के लिए निर्धारित करती है। अल्प अंतर।<ref name=":0">{{Cite book |title=Numerical Recipes: The Art of Scientific Computing |last1=Press |first1=W. H. |last2=Teukolsky |first2=S. A. |last3=Vetterling |first3=W. T. |last4=Flannery |first4=B. P. |publisher=Cambridge University Press |year=2007 |isbn=978-0-521-88068-8 |edition=3rd |location=New York (NY) |chapter=Section 16.1. Gaussian Mixture Models and ''k''-Means Clustering |chapter-url=http://apps.nrbook.com/empanel/index.html#pg=842 }}</ref>{{Rp|850}} प्रसरणों के अतिरिक्त, कठिन गॉसियन मिश्रण प्रारूपों के विशेष विषय में k-साधन माध्यम की तुल्यता दिखाने के लिए कठिन माध्यम अभिहस्तांकन का भी उपयोग किया जा सकता है।<ref>{{Cite book|title=Machine learning : a probabilistic perspective|last=Kevin P. Murphy|publisher=MIT Press|year=2012|isbn=978-0-262-30524-2|location=Cambridge, Mass.|oclc=810414751}}</ref>{{Rp|354|at=11.4.2.5}} इसका अर्थ यह नहीं है, कि K-साधनों की गणना करने के लिए गॉसियन मिश्रण प्रारूपों का उपयोग करना कुशल है, किन्तु केवल सैद्धांतिक संबंध है, और गॉसियन मिश्रण प्रारूपों को K-साधनों का सामान्यीकरण के रूप में व्याख्या किया जा सकता है। इसके विपरीत, कठिन डेटा पर गॉसियन मिश्रण प्रारूपों के लिए प्रारंभिक बिंदुओं का शोध करने के लिए k- साधन माध्यमग का उपयोग करने का विचार दिया गया है।<ref name=":0" />{{Rp|849}} | ||
K-माध्यिका | |||
=== के-एसवीडी === | === के-एसवीडी === | ||
{{Main|के-एसवीडी}} | {{Main|के-एसवीडी}}K- साधन एल्गोरिथ्म का अन्य सामान्यीकरण K-एसवीडी एल्गोरिथ्म है, जो कोडबुक सदिश के विरल रैखिक संयोजन के रूप में डेटा बिंदुओं का अनुमान लगाता है। K-साधन 1 के वजन के साथ एकल कोडबुक सदिश का उपयोग करने के विशेष स्थिति से मिलता है।<ref>{{Cite journal |last1=Aharon |first1=Michal|author1-link=Michal Aharon |last2=Elad |first2=Michael |last3=Bruckstein |first3=Alfred |year=2006 |title=K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation |url=http://www.cs.technion.ac.il/FREDDY/papers/120.pdf |journal=IEEE Transactions on Signal Processing |volume=54 |issue=11 |pages=4311 |bibcode=2006ITSP...54.4311A |doi=10.1109/TSP.2006.881199 |s2cid=7477309 }}</ref> | ||
K- साधन एल्गोरिथ्म का | |||
=== प्रधान घटक विश्लेषण === | === प्रधान घटक विश्लेषण === | ||
{{Main|Principal component analysis}} | {{Main|Principal component analysis}} | ||
{{math|<var>k</var>}}-अर्थ समूह, संकेतकों द्वारा निर्दिष्ट, प्रमुख घटक विश्लेषण (पीसीए) द्वारा दिया जाता है।<ref>{{cite journal |first1=Hongyuan |last1=Zha |first2=Chris |last2=Ding |first3=Ming |last3=Gu |first4=Xiaofeng |last4=He |first5=Horst D. |last5=Simon |date=December 2001 |title=''K'' के लिए वर्णक्रम संबंधी विश्राम - समूह का अर्थ है|url=http://ranger.uta.edu/~chqding/papers/Zha-Kmeans.pdf |journal=Neural Information Processing Systems Vol.14 (NIPS 2001) |pages=1057–1064 }}</ref><ref>{{cite journal |first1=Chris |last1=Ding |first2=Xiaofeng |last2=He |date=July 2004 |title=K- साधन प्रमुख घटक विश्लेषण के माध्यम से समूह|url=http://ranger.uta.edu/~chqding/papers/KmeansPCA1.pdf |pages=225–232 |journal=Proceedings of International Conference on Machine Learning (ICML 2004) }}</ref> अंतर्ज्ञान यह है कि k- साधन गोलाकार आकार (गेंद के जैसे) समूहों का वर्णन करते हैं। यदि डेटा में 2 समूह हैं, तो दो केन्द्रको को जोड़ने वाली रेखा सबसे उचित 1-आयामी प्रक्षेपण दिशा है, जो कि प्रथम पीसीए दिशा भी है। द्रव्यमान के केंद्र में रेखा का विभाजन समूहों को भिन्न करता है (यह असतत समूह संकेतक का निरंतर अनुमोचन है)। यदि डेटा में तीन समूह हैं, तो तीन समूह केन्द्रको द्वारा फैला हुआ है। 2-आयामी विमान सबसे सरल 2-डी प्रक्षेपण है। यह विमान प्रथम दो पीसीए आयामों द्वारा भी परिभाषित किया गया है। उचित रूप से भिन्न किए गए समूहों को गेंद के आकार के समूहों द्वारा प्रभावी रूप से प्रस्तुत किया जाता है और इस प्रकार K-साधनों द्वारा शोध किया जाता है। गैर-गेंद के आकार के समूहों को निकट होने पर भिन्न करना कठिन होता है। उदाहरण के लिए, अंतरिक्ष में परस्पर में गुंथे हुए दो अर्द्ध-चंद्रमा के आकार के समूह पीसीए उप-स्थान पर प्रक्षेपित होने पर उचित रूप से भिन्न नहीं होते हैं। K-माध्यिका से इस डेटा पर उचित प्रदर्शन करने की अपेक्षा नहीं की जानी चाहिए।<ref>{{cite journal |last1=Drineas |first1=Petros |first2=Alan M. |last2=Frieze |first3=Ravi |last3=Kannan |first4=Santosh |last4=Vempala |first5=Vishwanathan |last5=Vinay |year=2004 |title=एकवचन मूल्य अपघटन के माध्यम से बड़े रेखांकन को समूहित करना चाहिए। |url=http://www.cc.gatech.edu/~vempala/papers/dfkvv.pdf |journal=Machine Learning |volume=56 |issue=1–3 |pages=9–33 |doi=10.1023/b:mach.0000033113.59016.96 |s2cid=5892850 |access-date=2012-08-02 |doi-access=free }}</ref> इस कथन के प्रति उदाहरण प्रस्तुत करना सरल है, कि समूह केन्द्रक उप-स्थान मुख्य दिशाओं द्वारा फैला हुआ है।<ref>{{cite arXiv |eprint=1410.6801 |class=cs.DS |first1=Michael B. |last1=Cohen |first2=Sam |last2=Elder |title=''K'' के लिए आयाम में अभाव - अर्थात समूहों और निम्न श्रेणी निकट (परिशिष्ट बी) है।|year=2014|first3=Cameron |last3=Musco |first4=Christopher |last4=Musco |first5=Madalina |last5=Persu }}</ref> | |||
=== माध्य पारी समूह === | === माध्य पारी समूह === | ||
{{Main|Mean shift}} | {{Main|Mean shift}}बेसिक माध्य पारी माध्यम एल्गोरिदम इनपुट डेटा उपसमुच्चय के समान आकार के डेटा बिंदुओं का उपसमुच्चय बनाए रखता है। प्रारंभ में, इस उपसमुच्चय को इनपुट उपसमुच्चय से अनुकृति की जाती है। फिर इस समुच्चय को पुनरावृत्त रूप से उपसमुच्चय में उन बिंदुओं के माध्यम से परिवर्तित कर दिया जाता है जो उस बिंदु की दी गई दूरी के अंदर हैं। इसके विपरीत, k-माध्यिका इस अद्यतन उपसमुच्चय को k पॉइंट्स तक सीमित करता है जो सामान्यतः इनपुट डेटा समुच्चय में पॉइंट्स की संख्या से अधिक अल्प होता है, और इस उपसमुच्चय में प्रत्येक पॉइंट को इनपुट उपसमुच्चय में सभी पॉइंट्स के माध्यम से परिवर्तित कर देता है जो उस बिंदु के निकट हैं। किसी अन्य की तुलना में (उदाहरण के लिए प्रत्येक अद्यतन बिंदु के वोरोनोई विभाजन के अंदर) पारी माध्यम एल्गोरिदम जो कि K-माध्यिका के समान है, संभावना माध्य पारी कहा जाता है, इनपुट उपसमुच्चय में सभी बिंदुओं के माध्यम से प्रतिस्थापन के समय से निर्वाह होने वाले बिंदुओं के उपसमुच्चय को परिवर्तित कर देता है जो परिवर्तित उपसमुच्चय की दी गई दूरी के अंदर हैं।<ref name="Little20112">{{cite journal |last1=Little |first1=Max A. |last2=Jones |first2=Nick S. |year=2011 |title=Generalized Methods and Solvers for Piecewise Constant Signals: Part I |url=http://www.maxlittle.net/publications/pwc_filtering_arxiv.pdf |journal=[[Proceedings of the Royal Society A]] |volume=467 |issue=2135 |pages=3088–3114 |bibcode=2011RSPSA.467.3088L |doi=10.1098/rspa.2010.0671 |pmid=22003312 |pmc=3191861 }}</ref> K-साधनों पर औसत परिवर्तित के लाभों में से यह है कि माध्यमों की संख्या पूर्व-निर्दिष्ट नहीं है, क्योंकि औसत परिवर्तन केवल कुछ माध्यमों का शोध करने की संभावना है यदि केवल अल्प संख्या उपस्थित है। चूँकि, औसत परिवर्तन K-साधनों की तुलना में अधिक मंद हो सकता है, और तत्पश्चात बैंडविड्थ पैरामीटर के चयन की आवश्यकता होती है। | ||
बेसिक माध्य पारी | |||
=== स्वतंत्र घटक विश्लेषण === | === स्वतंत्र घटक विश्लेषण === | ||
{{Main|Independent component analysis}} | {{Main|Independent component analysis}}विरलता मान्यताओं के अनुसार और जब इनपुट डेटा [[सफेदी परिवर्तन]] के साथ प्री-प्रोसेस किया जाता है, तो k-माध्यिका रैखिक स्वतंत्र घटक विश्लेषण (ICA) कार्य का समाधान प्रस्तुत करता है। यह विशेषता अधिगम के लिए K-माध्यिका के सफल अनुप्रयोग की व्याख्या करने में सहायता करता है।<ref>{{cite journal|first1=Alon |last1=Vinnikov |first2=Shai |last2=Shalev-Shwartz |year=2014 |title=K-माध्यिका आईसीए निस्पंदन को रिकवर करता है जब स्वतंत्र घटक विरल होते हैं|url=http://www.cs.huji.ac.il/~shais/papers/KmeansICA_ICML2014.pdf |journal=Proceedings of the International Conference on Machine Learning (ICML 2014) }}</ref> | ||
विरलता मान्यताओं के अनुसार और जब इनपुट डेटा [[सफेदी परिवर्तन]] के साथ प्री-प्रोसेस किया जाता है, तो k-माध्यिका रैखिक स्वतंत्र घटक विश्लेषण (ICA) कार्य का समाधान प्रस्तुत करता है। यह विशेषता अधिगम के लिए K-माध्यिका के सफल अनुप्रयोग की व्याख्या करने में सहायता करता है।<ref>{{cite journal|first1=Alon |last1=Vinnikov |first2=Shai |last2=Shalev-Shwartz |year=2014 |title=K-माध्यिका आईसीए निस्पंदन को रिकवर करता है जब स्वतंत्र घटक विरल होते हैं|url=http://www.cs.huji.ac.il/~shais/papers/KmeansICA_ICML2014.pdf |journal=Proceedings of the International Conference on Machine Learning (ICML 2014) }}</ref> | |||
=== द्विपक्षीय निस्पंदन === | === द्विपक्षीय निस्पंदन === | ||
{{Main|Bilateral filter}} | {{Main|Bilateral filter}}K-साधन स्पष्ट रूप से मानता है कि इनपुट डेटा उपसमुच्चय का क्रम कोई फर्क नहीं पड़ता है। द्विपक्षीय निस्पंदन K-माध्यिका और [[ औसत पारी]] के समान है, जिसमें यह डेटा पॉइंट्स का समुच्चय बनाए रखता है जो कि माध्यमों द्वारा प्रतिस्थापित किया जाता है। चूँकि, द्विपक्षीय निस्पंदन (कर्नेल भारित) की गणना को प्रतिबंधित करता है, केवल उन बिंदुओं को सम्मिलित करने के लिए जो इनपुट डेटा के क्रम में निकट हैं।<ref name="Little20112" />यह इसे छवि डिनोइजिंग जैसी समस्याओं पर प्रारम्भ करता है, जहां छवि में पिक्सेल की स्थानिक व्यवस्था महत्वपूर्ण होती है। | ||
K-साधन स्पष्ट रूप से मानता है कि इनपुट डेटा उपसमुच्चय का क्रम कोई फर्क नहीं पड़ता है। द्विपक्षीय निस्पंदन K-माध्यिका और [[ औसत पारी]] के समान है, जिसमें यह डेटा पॉइंट्स का समुच्चय बनाए रखता है जो कि माध्यमों द्वारा प्रतिस्थापित किया जाता है। चूँकि, द्विपक्षीय निस्पंदन (कर्नेल भारित) की गणना को प्रतिबंधित करता है, केवल उन बिंदुओं को सम्मिलित करने के लिए जो इनपुट डेटा के क्रम में निकट हैं।<ref name="Little20112" />यह इसे छवि डिनोइजिंग जैसी समस्याओं पर प्रारम्भ करता है, जहां छवि में पिक्सेल की स्थानिक व्यवस्था महत्वपूर्ण होती है। | |||
== समान समस्याएं == | == समान समस्याएं == | ||
समूह फ़ंक्शंस को अल्प करने वाली चुकता त्रुटि के उपसमुच्च में K-[[ | समूह फ़ंक्शंस को अल्प करने वाली चुकता त्रुटि के उपसमुच्च में K-[[ medoids]] | k-मेडोइड्स एल्गोरिथ्म भी सम्मिलित है, दृष्टिकोण जो प्रत्येक समूह के केंद्र बिंदु को वास्तविक बिंदुओं में होने के लिए विवश करता है, अर्थात, यह केन्द्रक के स्थान पर मेडोइड्स का उपयोग करता है। | ||
== सॉफ्टवेयर कार्यान्वयन == | == सॉफ्टवेयर कार्यान्वयन == | ||
एल्गोरिथम के विभिन्न कार्यान्वयन प्रदर्शन अंतर प्रदर्शित करते हैं, परीक्षण डेटा उपसमुच्चय पर सबसे तीव्र 10 सेकंड में समाप्त होता है, सबसे मंद 25,988 सेकंड (~ 7 घंटे) लेता है।<ref name=":12" />अंतर को कार्यान्वयन गुणवत्ता, भाषा और संकलक अंतर, विभिन्न समाप्ति मानदंड और स्थिर स्तर, और त्वरण के लिए अनुक्रमणिका के उपयोग के लिए उत्तरदायी ठहराया जा सकता है। | एल्गोरिथम के विभिन्न कार्यान्वयन प्रदर्शन अंतर प्रदर्शित करते हैं, परीक्षण डेटा उपसमुच्चय पर सबसे तीव्र 10 सेकंड में समाप्त होता है, सबसे मंद 25,988 सेकंड (~ 7 घंटे) लेता है।<ref name=":12" />अंतर को कार्यान्वयन गुणवत्ता, भाषा और संकलक अंतर, विभिन्न समाप्ति मानदंड और स्थिर स्तर, और त्वरण के लिए अनुक्रमणिका के उपयोग के लिए उत्तरदायी ठहराया जा सकता है। | ||
=== मुफ़्त सॉफ़्टवेयर/ओपन सोर्स === | === मुफ़्त सॉफ़्टवेयर/ओपन सोर्स === | ||
नि:शुल्क और ओपन-सोर्स सॉफ़्टवेयर के अनुसार निम्नलिखित कार्यान्वयन उपलब्ध हैं। सार्वजनिक रूप से उपलब्ध स्रोत कोड के साथ मुफ़्त सोर्स सॉफ़्टवेयर अनुज्ञापत्र होते है।<sup><sup> | नि:शुल्क और ओपन-सोर्स सॉफ़्टवेयर के अनुसार निम्नलिखित कार्यान्वयन उपलब्ध हैं। सार्वजनिक रूप से उपलब्ध स्रोत कोड के साथ मुफ़्त सोर्स सॉफ़्टवेयर अनुज्ञापत्र होते है।<sup><sup> | ||
* Accord.NET में k-माध्यिका, k-माध्यिका++ और k-modes के लिए C# कार्यान्वयन सम्मिलित हैं। | * Accord.NET में k-माध्यिका, k-माध्यिका++ और k-modes के लिए C# कार्यान्वयन सम्मिलित हैं। | ||
* [[ALGLIB]] में k-माध्यिका और k-माध्यिका ++ के लिए समानांतर C++ और C# कार्यान्वयन सम्मिलित हैं। | * [[ALGLIB]] में k-माध्यिका और k-माध्यिका ++ के लिए समानांतर C++ और C# कार्यान्वयन सम्मिलित हैं। | ||
| Line 177: | Line 377: | ||
* [[KNIME]] में k-माध्यिका और k-medoids के लिए नोड होते हैं। | * [[KNIME]] में k-माध्यिका और k-medoids के लिए नोड होते हैं। | ||
* [[Apache Mahout]] में [[MapReduce]] आधारित k-माध्यिका सम्मिलित है। | * [[Apache Mahout]] में [[MapReduce]] आधारित k-माध्यिका सम्मिलित है। | ||
* [[ | * [[ mypack]] में K-साधनों का C ++ कार्यान्वयन सम्मिलित है। | ||
* [[जीएनयू ऑक्टेव]] में के-माध्यिका सम्मिलित हैं। | * [[जीएनयू ऑक्टेव]] में के-माध्यिका सम्मिलित हैं। | ||
* [[OpenCV]] में k- साधन कार्यान्वयन सम्मिलित है। | * [[OpenCV]] में k- साधन कार्यान्वयन सम्मिलित है। | ||
| Line 213: | Line 413: | ||
{{Reflist}} | {{Reflist}} | ||
Latest revision as of 12:31, 30 October 2023
K-माध्यम संचालन परिमाणीकरण की विधि है, जो मूल रूप से संकेत को आगे बढ़ाता है, जिसका उद्देश्य उपसमुच्चय N अवलोकनों को K माध्यमों में विभाजित करना है जिसमें प्रत्येक अवलोकन माध्यम (सांख्यिकी) से संबंधित हैI निकटतम माध्य (माध्यम केंद्र या माध्यम केन्द्रक) के साथ, माध्यम के प्रोटोटाइप के रूप में कार्य करता है। इसका परिणाम वोरोनोई कोशिकाओं में डेटा स्थान के विभाजन में होता है। k-अर्थात माध्यम भिन्नता को अल्प करता है, किन्तु नियमित यूक्लिडियन दूरियों को नहीं, जो कि अधिक कठिन वेबर समस्या होगी I माध्य त्रुटियों का अनुकूलन करता है, जबकि केवल ज्यामितीय माध्य यूक्लिडियन दूरी को अल्प करता है। उदाहरण के लिए, उत्तम यूक्लिडियन समाधान k-मेडियन और k-मेडोइड्स का उपयोग करके पाया जा सकता है।
समस्या कम्प्यूटेशनल रूप से कठिन है (एनपी-कठोरता) चूंकि, कुशल अनुमानी एल्गोरिदम स्थानीय इष्टतम में परिवर्तित हो जाते हैं। ये सामान्यतः 'K-साधन' एवं 'गाऊसी मिश्रण प्रारूपो' दोनों द्वारा नियोजित पुनरावृत्त शोधन दृष्टिकोण के माध्यम से गॉसियन वितरण के मिश्रण प्रारूप के लिए अपेक्षा-अधिकतमकरण एल्गोरिथ्म के समान हैं। वे दोनों डेटा को प्रारूप करने के लिए माध्यम केंद्रों का उपयोग करते हैं; चूंकि, k- का अर्थ है माध्यमिंग तुलनीय स्थानिक सीमा के माध्यमों का शोध करने के लिए किया जाता है, जबकि गॉसियन मिश्रण प्रारूप माध्यम्स को भिन्न-भिन्न आकार देने की अनुमति देता है।
अनियंत्रित k-अर्थात एल्गोरिदम का k-निकटतम परस्पर से संबंध है, k-निकटतम परस्पर वर्गीकारक, के लिए लोकप्रिय पर्यवेक्षितयंत्र अधिगम प्रविधि है, अर्थात नाम के कारण जिसे प्रायः भ्रमित किया जाता है। K द्वारा प्राप्त माध्यम केंद्रों में 1-निकटतम परस्पर वर्गीकारक को प्रारम्भ करने का अर्थात उपस्थित माध्यम में नए डेटा को वर्गीकृत करना है। इसे निकटतम केन्द्रक वर्गीकारक या रोक्चियो एल्गोरिथम के रूप में जाना जाता है।
विवरण
टिप्पणियों के उपसमुच्चय को देखते हुए (x1, x2, ..., xn), जहां प्रत्येक अवलोकन डी-आयामी वास्तविक सदिश है, k-अर्थात माध्यमिंग का उद्देश्य n अवलोकनों को k (≤ n) समुच्चय 's' = {s में विभाजित करना है1, s2, ..., sk} जिससे वर्गों के अंदर-माध्यम योग (WCSS) (अर्थात विचरण) को अल्प किया जा सके। औपचारिक रूप से इस उद्देश्य का शोध करना हैI
का आकार है , एवं सामान्य L2 मानदंड (गणित) है|
यह माध्यम में बिंदुओं के जोड़ीदार वर्ग विचलन को अल्प करने के बराबर है
इतिहास
k-माध्यिका शब्द का प्रथम बार उपयोग जेम्स मैकक्वीन ने 1967 में किया था।[1] चूँकि यह विचार 1956 में ह्यूगो स्टीनहॉस के पास वापस चला गया।[2] मानक एल्गोरिथम प्रथम बार 1957 में बेल लैब्स के स्टुअर्ट लॉयड द्वारा पल्स कोड मॉडुलेशन के लिए प्रविधियों के रूप में प्रस्तावित किया गया था, चूँकि इसे 1982 तक जर्नल लेख के रूप में प्रकाशित नहीं किया गया था।[3] 1965 में, एडवर्ड डब्ल्यू फोर्गी ने अनिवार्य रूप से विधि प्रकाशित की, यही कारण है कि इसे कभी-कभी लॉयड-फोर्गी एल्गोरिथम कहा जाता है।[4]
एल्गोरिदम
मानक एल्गोरिदम (बेवकूफ के-साधन)
सबसे सरल एल्गोरिथ्म पुनरावृत्त शोधन प्रविधि का उपयोग करता है। इसकी सर्वव्यापकता के कारण, इसे प्रायः k-अर्थात एल्गोरिथम कहा जाता हैI इसे विशेष रूप से कंप्यूटर विज्ञान समुदाय में लॉयड्स एल्गोरिथम के रूप में भी जाना जाता है। इसे कभी-कभी नैवे के-साधन के रूप में भी जाना जाता है I
कार्यभार चरण: प्रत्येक अवलोकन के समूह को निकटतम माध्य के साथ प्रस्तुत करता है। अल्प से अल्प वर्ग यूक्लिडियन दूरी के साथ।[7] (गणितीय रूप से, इसका अर्थ है साधनों द्वारा उत्पन्न वोरोनोई आरेख के अनुसार अवलोकनों को विभाजित करना।)
जहां प्रत्येक ठीक को प्रदान किया गया है , भले ही यह उनमें से दो या अधिक को सौंपा जा सकता है।
अद्यतन चरण: प्रत्येक समूह को अभिहस्तांकित किए गए अवलोकनों के लिए पुनर्गणना का अर्थ (केन्द्रक) होता है।
एल्गोरिथम अभिसरण तब होता है जब कार्यभार अब परिवर्तित नहीं होते हैं। इष्टतम का शोध करने के लिए एल्गोरिदम उत्तरदायी नहीं है।[8] एल्गोरिथम को प्रायः दूरी के आधार पर निकटतम समूह में वस्तु अभिहस्तांकित करने के रूप में प्रस्तुत किया जाता है। (स्क्वायर) यूक्लिडियन दूरी के अतिरिक्त किसी भिन्न दूरी फ़ंक्शन का उपयोग करने से एल्गोरिथम को अभिसरण से बाधित किया जा सकता है। K-माध्यिका के विभिन्न संशोधन जैसे गोलाकार K-माध्यिका और K-मेडोइड्स को अन्य दूरी उपायों का उपयोग करने की अनुमति देने के लिए प्रस्तावित किया गया है।
आरंभीकरण की विधि
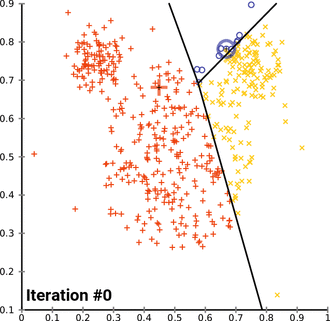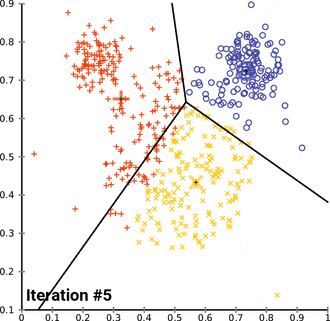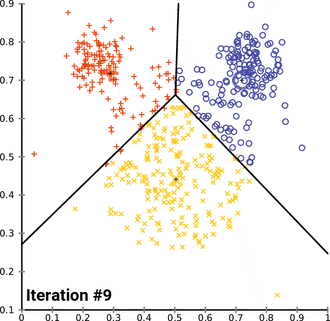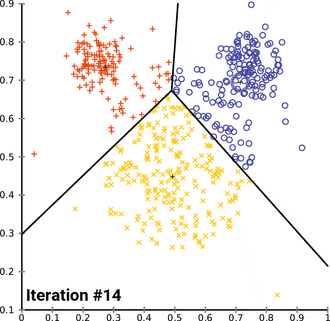
सामान्यतः उपयोग की जाने वाली आरंभीकरण विधियाँ और अनियमित विभाजन हैं। Forgy विधि यादृच्छिक रूप से डेटा समुच्चय से k अवलोकन का चयन करती है और प्रारंभिक साधनों के रूप में इनका उपयोग करती है। यादृच्छिक विभाजन विधि के पूर्व उचित रूप से प्रत्येक अवलोकन के लिए माध्यम प्रदान करती है और फिर अद्यतन चरण पर आगे बढ़ती है, इस प्रकार प्रारंभिक माध्य की गणना माध्यम के यादृच्छिक रूप से अभिहस्तांकित किए गए बिंदुओं के केन्द्रक के रूप में की जाती है। फोर्जी विधि प्रारंभिक साधनों को फैलाने की प्रवृत्ति रखती है, जबकि यादृच्छिक विभाजन उन सभी को डेटा समुच्चय के केंद्र के निकट रखता है। हैमरली एट अल के अनुसार, यादृच्छिक विभाजन विधि सामान्यतः एल्गोरिदम जैसे k-हार्मोनिक साधनों और k-साधनों के लिए उत्तम होती है। अपेक्षा अधिकतमकरण और मानक के-साधन एल्गोरिदम के लिए, प्रारंभिकरण की फोर्जी विधि उत्तम है। सेलेबी एट अल द्वारा व्यापक अध्ययन होता है। चूँकि, पाया गया कि फोर्जी, अनियमित विभाजन और मैक्सिमिन जैसे लोकप्रिय आरंभीकरण विधि प्रायः निकृष्ट प्रदर्शन करते हैं, जबकि ब्रैडली और फ़य्यद का दृष्टिकोण सर्वश्रेष्ठ माध्यम में निरंतर प्रदर्शन करता है और K-means++|k-means++ सामान्यतः उचित प्रदर्शन करता है।
- Demonstration of the standard algorithm
कठिनाई
डी आयामों में अवलोकन के लिए k-साधन समूह समस्या का इष्टतम समाधान का शोध करना है।
दो समूहों के लिए भी सामान्य यूक्लिडियन अंतरिक्ष (डी आयामों में) में NP कठिन होते है।
NP-कठिन सामान्य संख्या में समूह के लिए विमान में भी,
यदि k और d (आयाम) निश्चित हैं, तो समस्या का समय से निवारण किया जा सकता है।
O(ndk+1)
, जहां n समूह होने वाली संस्थाओं की संख्या है।
इस प्रकार, ऊपर दिए गए लॉयड के एल्गोरिथम जैसे विभिन्न अनुमानी एल्गोरिदम को सामान्यतः उपयोग किया जाता है।
लॉयड्स एल्गोरिथम (और अधिकांश रूपांतर) का बढनेवाला समय है।
O(nkdi)
, जहाँ:
n डी-रंगात्मक सदिश की संख्या है (क्लस्टर किया जाना है)।
कश्मीर समूहों की संख्या होती है।
I अभिसरण तक आवश्यक पुनरावृत्तियों की संख्या होती है।
समूह संरचना वाले डेटा पर, अभिसरण तक पुनरावृत्तियों की संख्या प्रायः अल्प होती है, और परिणाम केवल पूर्व दर्जन पुनरावृत्तियों के पश्चात थोड़ा सुधार करते हैं। इसलिए लॉयड के एल्गोरिथ्म को व्यवहार में प्रायः रैखिक जटिलता वाला माना जाता है, चूँकि अभिसरण तक किए जाने पर यह निकृष्टतम-प्रकरण कठिनता अधिबहुपद में होता है।
सबसे निकृष्ट स्थिति में, लॉयड के एल्गोरिथ्म की आवश्यकता होती है।
i=2Ω(n)
पुनरावृत्तियों, जिससे लॉयड के एल्गोरिथम की सबसे निकृष्ट स्थिति समय कठिन अधिबहुपद समय होता है।* लॉयड के K-माध्यिका एल्गोरिदम में बहुपद स्निग्ध बढनेवाला समय है। यह दिखाया गया है कि <रेफरी नाम = आर्थर, डेविड; मंथे, बी.; Roeglin, H. 20092 /> n बिंदुओं के इच्छानुकूल समुच्चय के लिए होता है।
[0,1]d
, यदि प्रत्येक बिंदु माध्य के साथ सामान्य वितरण द्वारा स्वतंत्र रूप से चिंतित है 0 और विचरण
σ2
, अपेक्षित चलने का समय k-अर्थात एल्गोरिद्म परिबद्ध है
O(n34k34d8log4(n)/σ6)
, जो बहुपद है। n, k, d और
1/σ
.
साधारण स्थितियों के लिए उत्तम सीमाएँ सिद्ध होती हैं। उदाहरण के लिए, यह दिखाया गया है कि k- साधन एल्गोरिथम का चलने का समय सीमाबद्ध है।
O(dn4M2)
के लिए n पूर्णांक जाली में अंक
{1,…,M}d
.
रूपांतर
Jenks प्राकृतिक टूटता अनुकूलन: K-माध्यिका यूनीवेट डेटा पर प्रारम्भ होता है
K-माध्यिका समूह औसत के अतिरिक्त प्रत्येक आयाम में औसत का उपयोग करता है, और इस प्रकार अर्घ्य करता है
L1
मानदंड (टैक्सीकैब ज्यामिति)।
K-माध्यिका (यह भी: माध्यिका के निकट विभाजन, पीएएम) माध्य के अतिरिक्त मेडॉइड का उपयोग करता है, और इस प्रकार इच्छानुकूल दूरी कार्यों के लिए दूरी का योग अल्प करता है।
फ़ज़ी समूह फ़ज़ी C-माध्यिका समूह K-माध्यिका का नरम वर्जन है, जहाँ प्रत्येक डेटा पॉइंट में प्रत्येक समूह से संबंधित फ़ज़ी श्रेणी होती है।
मिश्रण प्रारूप गॉसियन मिश्रण प्रारूप आश्वास-अधिकतमकरण एल्गोरिदम (ईएम एल्गोरिदम) के साथ प्रशिक्षित नियतात्मक कार्यभार के अतिरिक्त समूहों के लिए संभाव्य कार्यभार बनाए रखता है, और साधनों के अतिरिक्त बहुभिन्नरूपी गॉसियन वितरण करता है।
K-means++|k-means++ प्रारंभिक केंद्रों का इस प्रकार चयन करता है जो WCSS उद्देश्य पर सिद्ध ऊपरी सीमा देता है।
निस्पंदन एल्गोरिथ्म प्रत्येक k- साधन चरण को गति देने के लिए kd- ट्री का उपयोग करता है।
कुछ विधियाँ त्रिभुज असमानता का उपयोग करके प्रत्येक k- साधन चरण को गति देने का प्रयास करती हैं।* समूहों के मध्य बिंदुओं का आदान-प्रदान करके स्थानीय से संरक्षण करते है।* गोलाकार k- साधन क्लस्टरिंग एल्गोरिथ्म शाब्दिक डेटा के लिए उपयुक्त है।
पदानुक्रमित संस्करण जैसे द्विभाजित k- साधन, X-अर्थात समूह और G-अर्थात समूह पदानुक्रमित समूह, विभाजक समूह, और डेटा उपसमुच्चय में समूह की इष्टतम संख्या को स्वचालित रूप से निर्धारित करने का प्रयास भी कर सकता है।
समूह विश्लेषण आंतरिक मूल्यांकन उपाय जैसे सिल्हूट (समूह) डेटा उपसमुच्चय में समूह की संख्या निर्धारित करने में सहायक हो सकते हैं।
Minkowski भारित k-माध्यिका स्वचालित रूप से समूह विशिष्ट वैशिष्टय वेट की गणना करता है, सहज विचार का समर्थन करता है कि विशेषता में भिन्न-भिन्न सुविधाओं पर प्रासंगिकता की भिन्न-भिन्न उपाधि हो सकती है। इन भारों का उपयोग किसी दिए गए डेटा समुच्चय को स्तर करने के लिए भी किया जा सकता है, जिससे समूह की अपेक्षित संख्या में समूह वैधता सूचकांक को अनुकूलित करने की संभावना बढ़ जाती है।
अल्प-दल k- साधन डेटा उपसमुच्चय के लिए अल्प दल प्रतिमान का उपयोग करके भिन्नता जो मेमोरी में योग्य नहीं होती है।
ओत्सु की विधि
हार्टिगन-वोंग विधि
हार्टिगन और वोंग की विधिK-माध्यिका एल्गोरिदम की विविधता प्रदान करता है जो विभिन्न समाधान अद्यतनों के साथ न्यूनतम योग-वर्ग समस्या के स्थानीय न्यूनतम की ओर बढ़ता है। विधि स्थानीय खोज (अनुकूलन) है, जो मानक को भिन्न समूह में स्थानांतरित करने का प्रयत्न करती है जब तक कि यह प्रक्रिया उद्देश्य फंक्शन में सुधार करती है। जब उद्देश्य में सुधार के साथ किसी भिन्न समूह में कोई प्रतिमान स्थानांतरित नहीं किया जा सकता है, तो विधि समाप्त हो जाती है (स्थानीय न्यूनतम में)। शास्त्रीय के-साधन के समान ही, दृष्टिकोण अनुमानी बना हुआ है, क्योंकि यह आवश्यक रूप से आश्वासन नहीं देता है कि अंतिम समाधान विश्व स्तर पर इष्टतम है।
होने देना
φ(Sj)
की व्यक्तिगत वित्त हो
Sj
द्वारा परिभाषित
∑x∈Sj(x−μj)2
, साथ
μj
समूह का केंद्र होता है।
कार्यभार विधि: हार्टिगन और वोंग की विधि बिंदुओं को यादृच्छिक समूहों में विभाजित करके प्रारम्भ होती है
{Sj}j∈{1,⋯k}
।
अद्यतन चरण: आगामी यह निर्धारित करता है
n,m∈{1,…,k}
और
x∈Sn
जिसके लिए निम्नलिखित कार्य अधिकतम तक पहुँचता है।
Δ(m,n,x)=φ(Sn)+φ(Sm)−φ(Sn∖{x})−φ(Sm∪{x})
के लिए
x,n,m
जो इस अधिकतम तक पहुँचे,
x
समूहों से चलता है
Sn
समूह को
Sm
निर्धारित करता है।
समाप्ति: एल्गोरिथम टर्मिनेट होता है
Δ(m,n,x)
सभी के लिए शून्य से अर्घ्य है
x,n,m
.
विभिन्न चाल स्वीकृति रणनीतियों का उपयोग किया जा सकता है। पूर्व-सुधार की रणनीति में, किसी भी सुधार के स्थानांतरण को प्रारम्भ किया जा सकता है, जबकि सर्वोत्तम-सुधार की रणनीति में, सभी संभव स्थानांतरणों का पुनरावृत्त रूप से परीक्षण किया जाता है और प्रत्येक पुनरावृत्ति पर केवल सर्वश्रेष्ठ को प्रारम्भ किया जाता है। पूर्व दृष्टिकोण गति का समर्थन करता है, दृष्टिकोण सामान्यतः अतिरिक्त कम्प्यूटेशनल समय के मूल्य पर समाधान की गुणवत्ता का पक्ष लेता है। कार्यक्रम
Δ
स्थानांतरण के परिणाम की गणना करने के लिए उपयोग किया जाता है, समानता का उपयोग करके भी कुशलतापूर्वक मूल्यांकन किया जा सकता है।
Δ(x,n,m)=∣Sn∣∣Sn∣−1⋅‖μn−x‖2−∣Sm∣∣Sm∣+1⋅‖μm−x‖2.
वैश्विक अनुकूलन और मेटाह्यूरिस्टिक्स
शास्त्रीय k- साधन एल्गोरिथ्म एवं इसकी विविधताओं को "केंद्र"> के रूप में परिभाषित न्यूनतम-योग-वर्ग समूह समस्या के केवल स्थानीय न्यूनतम में परिवर्तित करने के लिए जाना जाता है। कई अध्ययनों ने एल्गोरिथम के अभिसरण व्यवहार में सुधार करने एवं वैश्विक इष्टतम (या अल्प से अल्प, उत्तम गुणवत्ता के स्थानीय न्यूनतम) प्राप्त करने की संभावना को अधिकतम करने का प्रयत्न किया है। पूर्व अनुभागों में वर्णन किया गया था। आरंभीकरण एवं पुनः आरंभ करने की प्रविधि उत्तम समाधान का शोध करने के लिए विकल्प हैं। शाखा एवं बंधन एवं अर्ध निश्चित प्रोग्रामिंग पर आधारित वैश्विक अनुकूलन एल्गोरिदम ने 4,177 संस्थाओं एवं 20,531 सुविधाओं के साथ डेटासमुच्चय के लिए सिद्ध रूप से इष्टतम समाधान प्रस्तुत किए हैं।[5] जैसा कि अपेक्षित था, उपजात अनुकूलन समस्या की NP-कठोरता के कारण, K-साधनों के लिए इष्टतम एल्गोरिदम का कम्प्यूटेशनल समय इस आकार से तीव्र गति से बढ़ता है। अन्य अनुमानों की गुणवत्ता का मूल्यांकन करने के लिए, अल्प एवं मध्यम स्तर के लिए इष्टतम समाधान अभी भी बेंचमार्क उपकरण के रूप में मूल्यवान हैं। नियंत्रित कम्प्यूटेशनल समय के अंदर उच्च-गुणवत्ता वाले स्थानीय मिनिमा का शोध करने के लिए, किन्तु इष्टतमता का कथन के बिना, अन्य कार्यों ने मेटाह्यूरिस्टिक्स एवं अन्य वैश्विक अनुकूलन प्रविधियों की जानकारी ज्ञात की है। उदाहरण के लिए, वृद्धिशील दृष्टिकोण एवं उत्तल अनुकूलन के आधार पर,[6] यादृच्छिक आदान-प्रदान[7] (अर्थात, पुनरावृत्त स्थानीय शोध), परिवर्तनशील परस्पर शोध[8] एवं आनुवंशिक एल्गोरिदम।[9][10] यह वास्तव में ज्ञात है कि न्यूनतम सम-वर्ग माध्यमिंक समस्या का उत्तम स्थानीय न्यूनतम का शोध करने से उच्च आयाम वाले वैशिष्टय अंतर में माध्यम संरचनाओं को पुनर्प्राप्त करने में विफलता एवं सफलता के मध्य अंतर हो सकता है।
उल्लेख
होते ह

- यूक्लिडियन दूरी का उपयोग मीट्रिक (गणित) के रूप में किया जाता है और विचरण का उपयोग समूह स्कैटर के माप के रूप में किया जाता है।
- समूह k की संख्या इनपुट पैरामीटर है। k का अनुचित विकल्प निकृष्ट परिणाम दे सकता है। इसीलिए, k-माध्यिका करते समय, डेटा उपसमुच्चय में समूह की संख्या निर्धारित करने के लिए नैदानिक चेक चलाना महत्वपूर्ण है।
- स्थानीय न्यूनतम के अभिसरण से विपरीत (गलत) परिणाम उत्पन्न हो सकते हैं (चित्र में उदाहरण देखें)।
K- साधन की प्रमुख सीमा इसका समूह प्रारूप है। अवधारणा गोलाकार समूहों पर आधारित है जो वियोज्य हैं जिससे माध्य समूह केंद्र की ओर अभिसरण होता है। समूह समान आकार के होने की अपेक्षा है, जिससे निकटतम समूह केंद्र का कार्यभार सही हो। उदाहरण के लिए जब k- साधन को मान के साथ प्रारम्भ किया जाता है। प्रसिद्ध आइरिस फूल डेटा उपसमुच्चय पर, परिणाम प्रायः डेटा उपसमुच्चय में निहित तीन आइरिस (पौधे) प्रजातियों को भिन्न करने में विफल रहता है। साथ , दो दृश्य समूहों (दो प्रजातियों वाला ) का शोध किया जायेगा, जबकि साथ में दो समूहों को दो समान भागों में विभाजित किया जाएगा। वास्तव में, डेटा उपसमुच्चय में 3 वर्ग होने के पश्चात, इस डेटा उपसमुच्चय के लिए अधिक उपयुक्त है। किसी भी अन्य समूह एल्गोरिदम के साथ, K-साधन परिणाम यह मानते हैं कि डेटा कुछ मानदंडों को पूर्ण करता है। यह कुछ डेटा उपसमुच्चय पर उचित कार्य करता है और दूसरों पर विफल रहता है।
K-साधनों का परिणाम समूह साधनों के वोरोनोई आरेख के रूप में देखा जा सकता है। चूंकि डेटा समूह माध्यमों के मध्य अर्द्ध मार्ग में विभाजित होता है, इससे उप-इष्टतम विभाजन हो सकता है जैसा कि माउस उदाहरण में देखा जा सकता है। अपेक्षा-अधिकतमकरण एल्गोरिथ्म (तर्कसंगत रूप से k-साधनों का सामान्यीकरण) द्वारा उपयोग किए जाने वाले गॉसियन प्रारूप प्रसरण और सहप्रसरण दोनों होने के कारण अधिक नमनीय होते हैं। इस प्रकार EM परिणाम चर आकार के समूहों को k-साधनों के साथ-साथ सहसंबद्ध समूहों (इस उदाहरण में नहीं) से उत्तम समायोजित करने में सक्षम है। प्रतिपक्ष में, EM को बड़ी संख्या में मुक्त मापदंडों के अनुकूलन की आवश्यकता होती है और लुप्त हो रहे समूहों से वातानुकूलित सहप्रसरण मैट्रिक्स के कारण कुछ पद्धतिगत विषयो को प्रस्तुत करता है। K- साधन गैर-पैरामीट्रिक बायेसियन अनुमान से निकटता से संबंधित है।[11]
अनुप्रयोग
k-माध्यिका समूह अपेक्षाकृत बड़े डेटा उपसमुच्चय पर प्रारम्भ करना सरल है, विशेष रूप से जब ह्यूरिस्टिक्स जैसे कि लॉयड्स एल्गोरिथम का उपयोग करते हैं। इसे कई अन्य डोमेन के मध्य व्यापार विभाजन, कंप्यूटर दृष्टि और खगोल विज्ञान में सफलतापूर्वक उपयोग किया गया है। यह प्रायः अन्य एल्गोरिदम के लिए प्रसंस्करण चरण के रूप में उपयोग किया जाता है, उदाहरण के लिए प्रारंभिक व्यवस्था के प्रारूप का शोध करने के लिए होता है।
सदिश परिमाणीकरण
k-साधन एकल प्रसंस्करण से उत्पन्न होता है, एवं अभी भी इस डोमेन में उपयोग होता है। उदाहरण के लिए, कंप्यूटर चित्रलेख में, रंग परिमाणीकरणछ व ि क े प ै ल े ट ( क ंप्यूटिंग) रंगों की निश्चित संख्या में अल्प करने का कार्य है। इस कार्य के लिए k-माध्यि एल्गोरिदम का सरलता से उपयोग किया जा सकता है एवं प्रतिस्पर्धी परिणाम उत्पन्न करता है। इस दृष्टिकोण के लिए उपयोग का विषय छवि विभाजन है। सदिश परिमाणीकरण के अन्य उपयोगों में प्रतिरूपकरण (सांख्यिकी) | गैर-यादृच्छिक प्रतिरूपकरण सम्मिलित है, क्योंकि k-साधन का उपयोग आगे के विश्लेषण के लिए बड़े डेटा समुच्चय से k भिन्न किन्तु प्रोटोटाइपिक वस्तुओं का चयन करने के लिए सरलता से किया जा सकता है।
समूह विश्लेषण
माध्यम विश्लेषण में, k- साधन एल्गोरिथ्म का उपयोग इनपुट डेटा समुच्चय को k विभाजन (माध्यम) में विभाजित करने के लिए किया जा सकता है।चूँकि, शुद्ध k-साधन एल्गोरिदम अधिक नमनीय नहीं है, और (कि जब ऊपर के रूप में सदिश अनुमान वास्तव में वांछित उपयोग विषय है)। विशेष रूप से, पैरामीटर k का चयन कठिन माना जाता है (जैसा कि ऊपर वर्णन किया गया है) जब बाहरी बाधाओं द्वारा नहीं दिया जाता है। इसका उपयोग इच्छानुकूल दूरी के कार्यों या गैर-संख्यात्मक डेटा के साथ नहीं किया जा सकता है। इन उपयोग विषयो के लिए, कई अन्य एल्गोरिदम श्रेष्ठ हैं।
विशेष अधिगम
k-means समूह का उपयोग विशेष अधिगम (या शब्दकोश सीखना ) विधि के रूप में किया गया है, या तो पर्यवेक्षित अधिगम या अनियंत्रित शिक्षा ।[12] मूल दृष्टिकोण सबसे प्रथम इनपुट प्रशिक्षण डेटा (जिसे लेबल करने की आवश्यकता नहीं है) का उपयोग करके k- साधन समूह प्रतिनिधित्व को प्रशिक्षित करना है। किसी भी इनपुट डेटा को नए विशेष स्थान में परियोजना करने के लिए, संकेतीकरण फ़ंक्शन, जैसे कि केन्द्रक स्थानों के साथ डेटम का थ्रेशोल्ड आव्यूह-उत्पाद, डेटम से प्रत्येक केन्द्रक तक की दूरी की गणना करता है, या बस निकटतम के लिए संकेतक फ़ंक्शन केन्द्रक,[12][13] या दूरी का कुछ सहज परिवर्तन होता है।[14] वैकल्पिक रूप से, रेडियल आधार फ़ंक्शन के माध्यम से प्रतिमान-समूह दूरी को परिवर्तित करने से दीप्तिमान आधार फंक्शन नेटवर्क की छिपी हुई परत प्राप्त होती है।[15] प्राकृतिक भाषा प्रसंस्करण (विशेष रूप से नामित इकाई पहचान के लिए) में अर्ध-पर्यवेक्षित सीखने के लिए K-साधनों के इस उपयोग को सरल, रैखिक वर्गीकरण के साथ सफलतापूर्वक जोड़ा गया है।[16] और कंप्यूटर दृष्टि में वस्तु रिकग्निशन मानक पर, ऑटोएनकोडर और [प्रतिबंधित विद्युत मशीन] जैसे अधिक परिष्कृत विशेष अधिगम दृष्टिकोण के साथ तुलनात्मक प्रदर्शन प्रदर्शित करने के लिए पाया गया।[14]चूँकि, समान प्रदर्शन के लिए इसे सामान्यतः अधिक डेटा की आवश्यकता होती है, क्योंकि प्रत्येक डेटा बिंदु केवल सुविधा में योगदान देता है।[12]
अन्य एल्गोरिदम से संबंध
गॉसियन मिश्रण प्रारूप
K-माध्यिका माध्यम के लिए मंद मानक एल्गोरिथ्म, और इसके संबद्ध अपेक्षा-अधिकतमकरण एल्गोरिथ्म, गॉसियन मिश्रण प्रारूप का विशेष विषय है। विशेष रूप से, सीमित स्थिति जब सभी सहप्रसरणों को विकर्ण, समान और अपरिमेय होने के लिए निर्धारित करती है। अल्प अंतर।[17]: 850 प्रसरणों के अतिरिक्त, कठिन गॉसियन मिश्रण प्रारूपों के विशेष विषय में k-साधन माध्यम की तुल्यता दिखाने के लिए कठिन माध्यम अभिहस्तांकन का भी उपयोग किया जा सकता है।[18]: 354, 11.4.2.5 इसका अर्थ यह नहीं है, कि K-साधनों की गणना करने के लिए गॉसियन मिश्रण प्रारूपों का उपयोग करना कुशल है, किन्तु केवल सैद्धांतिक संबंध है, और गॉसियन मिश्रण प्रारूपों को K-साधनों का सामान्यीकरण के रूप में व्याख्या किया जा सकता है। इसके विपरीत, कठिन डेटा पर गॉसियन मिश्रण प्रारूपों के लिए प्रारंभिक बिंदुओं का शोध करने के लिए k- साधन माध्यमग का उपयोग करने का विचार दिया गया है।[17]: 849के-एसवीडी
K- साधन एल्गोरिथ्म का अन्य सामान्यीकरण K-एसवीडी एल्गोरिथ्म है, जो कोडबुक सदिश के विरल रैखिक संयोजन के रूप में डेटा बिंदुओं का अनुमान लगाता है। K-साधन 1 के वजन के साथ एकल कोडबुक सदिश का उपयोग करने के विशेष स्थिति से मिलता है।[19]
प्रधान घटक विश्लेषण
k-अर्थ समूह, संकेतकों द्वारा निर्दिष्ट, प्रमुख घटक विश्लेषण (पीसीए) द्वारा दिया जाता है।[20][21] अंतर्ज्ञान यह है कि k- साधन गोलाकार आकार (गेंद के जैसे) समूहों का वर्णन करते हैं। यदि डेटा में 2 समूह हैं, तो दो केन्द्रको को जोड़ने वाली रेखा सबसे उचित 1-आयामी प्रक्षेपण दिशा है, जो कि प्रथम पीसीए दिशा भी है। द्रव्यमान के केंद्र में रेखा का विभाजन समूहों को भिन्न करता है (यह असतत समूह संकेतक का निरंतर अनुमोचन है)। यदि डेटा में तीन समूह हैं, तो तीन समूह केन्द्रको द्वारा फैला हुआ है। 2-आयामी विमान सबसे सरल 2-डी प्रक्षेपण है। यह विमान प्रथम दो पीसीए आयामों द्वारा भी परिभाषित किया गया है। उचित रूप से भिन्न किए गए समूहों को गेंद के आकार के समूहों द्वारा प्रभावी रूप से प्रस्तुत किया जाता है और इस प्रकार K-साधनों द्वारा शोध किया जाता है। गैर-गेंद के आकार के समूहों को निकट होने पर भिन्न करना कठिन होता है। उदाहरण के लिए, अंतरिक्ष में परस्पर में गुंथे हुए दो अर्द्ध-चंद्रमा के आकार के समूह पीसीए उप-स्थान पर प्रक्षेपित होने पर उचित रूप से भिन्न नहीं होते हैं। K-माध्यिका से इस डेटा पर उचित प्रदर्शन करने की अपेक्षा नहीं की जानी चाहिए।[22] इस कथन के प्रति उदाहरण प्रस्तुत करना सरल है, कि समूह केन्द्रक उप-स्थान मुख्य दिशाओं द्वारा फैला हुआ है।[23]
माध्य पारी समूह
बेसिक माध्य पारी माध्यम एल्गोरिदम इनपुट डेटा उपसमुच्चय के समान आकार के डेटा बिंदुओं का उपसमुच्चय बनाए रखता है। प्रारंभ में, इस उपसमुच्चय को इनपुट उपसमुच्चय से अनुकृति की जाती है। फिर इस समुच्चय को पुनरावृत्त रूप से उपसमुच्चय में उन बिंदुओं के माध्यम से परिवर्तित कर दिया जाता है जो उस बिंदु की दी गई दूरी के अंदर हैं। इसके विपरीत, k-माध्यिका इस अद्यतन उपसमुच्चय को k पॉइंट्स तक सीमित करता है जो सामान्यतः इनपुट डेटा समुच्चय में पॉइंट्स की संख्या से अधिक अल्प होता है, और इस उपसमुच्चय में प्रत्येक पॉइंट को इनपुट उपसमुच्चय में सभी पॉइंट्स के माध्यम से परिवर्तित कर देता है जो उस बिंदु के निकट हैं। किसी अन्य की तुलना में (उदाहरण के लिए प्रत्येक अद्यतन बिंदु के वोरोनोई विभाजन के अंदर) पारी माध्यम एल्गोरिदम जो कि K-माध्यिका के समान है, संभावना माध्य पारी कहा जाता है, इनपुट उपसमुच्चय में सभी बिंदुओं के माध्यम से प्रतिस्थापन के समय से निर्वाह होने वाले बिंदुओं के उपसमुच्चय को परिवर्तित कर देता है जो परिवर्तित उपसमुच्चय की दी गई दूरी के अंदर हैं।[24] K-साधनों पर औसत परिवर्तित के लाभों में से यह है कि माध्यमों की संख्या पूर्व-निर्दिष्ट नहीं है, क्योंकि औसत परिवर्तन केवल कुछ माध्यमों का शोध करने की संभावना है यदि केवल अल्प संख्या उपस्थित है। चूँकि, औसत परिवर्तन K-साधनों की तुलना में अधिक मंद हो सकता है, और तत्पश्चात बैंडविड्थ पैरामीटर के चयन की आवश्यकता होती है।स्वतंत्र घटक विश्लेषण
विरलता मान्यताओं के अनुसार और जब इनपुट डेटा सफेदी परिवर्तन के साथ प्री-प्रोसेस किया जाता है, तो k-माध्यिका रैखिक स्वतंत्र घटक विश्लेषण (ICA) कार्य का समाधान प्रस्तुत करता है। यह विशेषता अधिगम के लिए K-माध्यिका के सफल अनुप्रयोग की व्याख्या करने में सहायता करता है।[25]
द्विपक्षीय निस्पंदन
K-साधन स्पष्ट रूप से मानता है कि इनपुट डेटा उपसमुच्चय का क्रम कोई फर्क नहीं पड़ता है। द्विपक्षीय निस्पंदन K-माध्यिका और औसत पारी के समान है, जिसमें यह डेटा पॉइंट्स का समुच्चय बनाए रखता है जो कि माध्यमों द्वारा प्रतिस्थापित किया जाता है। चूँकि, द्विपक्षीय निस्पंदन (कर्नेल भारित) की गणना को प्रतिबंधित करता है, केवल उन बिंदुओं को सम्मिलित करने के लिए जो इनपुट डेटा के क्रम में निकट हैं।[24]यह इसे छवि डिनोइजिंग जैसी समस्याओं पर प्रारम्भ करता है, जहां छवि में पिक्सेल की स्थानिक व्यवस्था महत्वपूर्ण होती है।समान समस्याएं
समूह फ़ंक्शंस को अल्प करने वाली चुकता त्रुटि के उपसमुच्च में K-medoids | k-मेडोइड्स एल्गोरिथ्म भी सम्मिलित है, दृष्टिकोण जो प्रत्येक समूह के केंद्र बिंदु को वास्तविक बिंदुओं में होने के लिए विवश करता है, अर्थात, यह केन्द्रक के स्थान पर मेडोइड्स का उपयोग करता है।
सॉफ्टवेयर कार्यान्वयन
एल्गोरिथम के विभिन्न कार्यान्वयन प्रदर्शन अंतर प्रदर्शित करते हैं, परीक्षण डेटा उपसमुच्चय पर सबसे तीव्र 10 सेकंड में समाप्त होता है, सबसे मंद 25,988 सेकंड (~ 7 घंटे) लेता है।[26]अंतर को कार्यान्वयन गुणवत्ता, भाषा और संकलक अंतर, विभिन्न समाप्ति मानदंड और स्थिर स्तर, और त्वरण के लिए अनुक्रमणिका के उपयोग के लिए उत्तरदायी ठहराया जा सकता है।
मुफ़्त सॉफ़्टवेयर/ओपन सोर्स
नि:शुल्क और ओपन-सोर्स सॉफ़्टवेयर के अनुसार निम्नलिखित कार्यान्वयन उपलब्ध हैं। सार्वजनिक रूप से उपलब्ध स्रोत कोड के साथ मुफ़्त सोर्स सॉफ़्टवेयर अनुज्ञापत्र होते है।
- Accord.NET में k-माध्यिका, k-माध्यिका++ और k-modes के लिए C# कार्यान्वयन सम्मिलित हैं।
- ALGLIB में k-माध्यिका और k-माध्यिका ++ के लिए समानांतर C++ और C# कार्यान्वयन सम्मिलित हैं।
- एंड्रॉइड (ऑपरेटिंग प्रणाली)ओपन-सोर्स समुदाय में K-साधनों के लिए जावा कार्यान्वयन सम्मिलित है।
- क्राइमस्टैट दो स्थानिक के-माध्यिका एल्गोरिदम को प्रारम्भ करता है, जिनमें से उपयोगकर्ता को प्रारंभिक स्थानों को परिभाषित करने की अनुमति देता है।
- ईएलकेआई में के-माध्यिका (लॉयड और मैकक्वीन पुनरावृत्ति के साथ-साथ विभिन्न आरंभीकरण जैसे कि K-माध्यिका ++ आरंभीकरण) और विभिन्न अधिक उन्नत समूह एल्गोरिदम सम्मिलित हैं।
- मुस्कान में के-माध्यिका और कई अन्य एल्गोरिदम और परिणाम प्रत्योक्षकरण (जावा, कोटलिन और स्कैला के लिए) सम्मिलित हैं।
- जूलिया भाषा में जूलियास्टैट्स समूह में K-साधन कार्यान्वयन सम्मिलित है।
- KNIME में k-माध्यिका और k-medoids के लिए नोड होते हैं।
- Apache Mahout में MapReduce आधारित k-माध्यिका सम्मिलित है।
- mypack में K-साधनों का C ++ कार्यान्वयन सम्मिलित है।
- जीएनयू ऑक्टेव में के-माध्यिका सम्मिलित हैं।
- OpenCV में k- साधन कार्यान्वयन सम्मिलित है।
- ऑरेंज (सॉफ्टवेयर) में K-माध्यिका समूह के लिए घटक सम्मिलित है जिसमें K और समूह सिल्हूट स्कोरिंग का स्वत: चयन होता है।
- PSPP में k- साधन सम्मिलित हैं, QUICK CLUSTER कमांड डेटासेट पर k- साधन क्लस्टरिंग करता है।
- R (प्रोग्रामिंग भाषा) में तीन k-माध्यिका रूपांतर होते हैं।
- SciPy और scikit-learn में कई k- साधन कार्यान्वयन सम्मिलित हैं।
- Apache Spark MLlib वितरित k- साधन एल्गोरिथम प्रारम्भ करता है।
- टॉर्च (मशीन अधिगम) में अन-अप संकुल होता है जो k- साधन समूह प्रदान करता है।
- वीका (मशीन लर्निंग) में K-माध्यिका और X-माध्यिका सम्मिलित हैं।
प्रभुत्व
निम्नलिखित कार्यान्वयन प्रभुत्व सॉफ्टवेयर अनुज्ञापत्र अनुबंध के अनुसार उपलब्ध हैं, और सार्वजनिक रूप से उपलब्ध स्रोत कोड नहीं हो सकते हैं।- अयस्दि
- मेथेमेटिका
- अर्थात
- ओरिजिन (डाटा एनालिसिस सॉफ्टवेयर)
- रपीडमीनेर
- सैप हाना
- एसएएस प्रणाली
- सपसस
- सताता
यह भी देखें
- बीएफआर एल्गोरिदम
- केन्द्रक वोरोनोई चौकोर
- सिर/पूंछ टूट जाती है
- K Q-समतल भूमि
- लिंडे-बुजो-ग्रे एल्गोरिदम
- स्व-आयोजन मानचित्र
संदर्भ
- ↑ MacQueen, J. B. (1967). बहुभिन्नरूपी टिप्पणियों के वर्गीकरण और विश्लेषण के लिए कुछ विधिया होती है।. Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability. Vol. 1. University of California Press. pp. 281–297. MR 0214227. Zbl 0214.46201. Retrieved 2009-04-07.
- ↑ Steinhaus, Hugo (1957). "Sur la division des corps matériels en parties". Bull. Acad. Polon. Sci. (in français). 4 (12): 801–804. MR 0090073. Zbl 0079.16403.
- ↑ Lloyd, Stuart P. (1957). "पीसीएम में अल्प से अल्प वर्ग परिमाणीकरण होते है". Bell Telephone Laboratories Paper. Published in journal much later: Lloyd, Stuart P. (1982). "Least squares quantization in PCM" (PDF). IEEE Transactions on Information Theory. 28 (2): 129–137. CiteSeerX 10.1.1.131.1338. doi:10.1109/TIT.1982.1056489. S2CID 10833328. Retrieved 2009-04-15.
- ↑ Forgy, Edward W. (1965). "Cluster analysis of multivariate data: efficiency versus interpretability of classifications". Biometrics. 21 (3): 768–769. JSTOR 2528559.
- ↑ Piccialli, Veronica; Sudoso, Antonio M.; Wiegele, Angelika (2022-03-28). "SOS-SDP: An Exact Solver for Minimum Sum-of-Squares Clustering". INFORMS Journal on Computing (in English). 34 (4): 2144–2162. arXiv:2104.11542. doi:10.1287/ijoc.2022.1166. ISSN 1091-9856. S2CID 233388043.
- ↑ Bagirov, A. M.; Taheri, S.; Ugon, J. (2016). "न्यूनतम सम-वर्ग समूह समस्याओं के लिए गैर-अरूक्ष डीसी प्रोग्रामिंग दृष्टिकोण". Pattern Recognition. 53: 12–24. Bibcode:2016PatRe..53...12B. doi:10.1016/j.patcog.2015.11.011.
- ↑ Fränti, Pasi (2018). "यादृच्छिक स्वैप क्लस्टरिंग की दक्षता". Journal of Big Data. 5 (1): 1–21. doi:10.1186/s40537-018-0122-y.
- ↑ Hansen, P.; Mladenovic, N. (2001). "J-Means: A new local search heuristic for minimum sum of squares clustering". Pattern Recognition. 34 (2): 405–413. Bibcode:2001PatRe..34..405H. doi:10.1016/S0031-3203(99)00216-2.
- ↑ Krishna, K.; Murty, M. N. (1999). "आनुवंशिक K-अर्थात एल्गोरिथम होते है।journal= IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics". 29 (3): 433–439. doi:10.1109/3477.764879. PMID 18252317.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Gribel, Daniel; Vidal, Thibaut (2019). "HG-means: A scalable hybrid metaheuristic for minimum sum-of-squares clustering". Pattern Recognition. 88: 569–583. arXiv:1804.09813. doi:10.1016/j.patcog.2018.12.022. S2CID 13746584.
- ↑ Kulis, Brian; Jordan, Michael I. (2012-06-26). Revisiting k-means: new algorithms via Bayesian nonparametrics (PDF). pp. 1131–1138. ISBN 9781450312851.
{{cite book}}:|journal=ignored (help) - ↑ 12.0 12.1 12.2 Coates, Adam; Ng, Andrew Y. (2012). "Learning feature representations with k-means" (PDF). In Montavon, G.; Orr, G. B.; Müller, K.-R. (eds.). Neural Networks: Tricks of the Trade. Springer.
- ↑ Csurka, Gabriella; Dance, Christopher C.; Fan, Lixin; Willamowski, Jutta; Bray, Cédric (2004). मुख्य बिंदुओं के बैग के साथ दृश्य वर्गीकरण (PDF). ECCV Workshop on Statistical Learning in Computer Vision.
- ↑ 14.0 14.1 Coates, Adam; Lee, Honglak; Ng, Andrew Y. (2011). उपेक्षा विशेष अधिगम में एकल-स्तर नेटवर्क के विश्लेषण (PDF). International Conference on Artificial Intelligence and Statistics (AISTATS). Archived from the original (PDF) on 2013-05-10.
- ↑ Schwenker, Friedhelm; Kestler, Hans A.; Palm, Günther (2001). "दीप्तिमान-आधार-फंक्शन नेटवर्क के लिए सीखने के तीन चरण". Neural Networks. 14 (4–5): 439–458. CiteSeerX 10.1.1.109.312. doi:10.1016/s0893-6080(01)00027-2. PMID 11411631.
- ↑ Lin, Dekang; Wu, Xiaoyun (2009). भेदभावपूर्ण सीखने के लिए वाक्यांश समूह (PDF). Annual Meeting of the ACL and IJCNLP. pp. 1030–1038.
- ↑ 17.0 17.1 Press, W. H.; Teukolsky, S. A.; Vetterling, W. T.; Flannery, B. P. (2007). "Section 16.1. Gaussian Mixture Models and k-Means Clustering". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York (NY): Cambridge University Press. ISBN 978-0-521-88068-8.
- ↑ Kevin P. Murphy (2012). Machine learning : a probabilistic perspective. Cambridge, Mass.: MIT Press. ISBN 978-0-262-30524-2. OCLC 810414751.
- ↑ Aharon, Michal; Elad, Michael; Bruckstein, Alfred (2006). "K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation" (PDF). IEEE Transactions on Signal Processing. 54 (11): 4311. Bibcode:2006ITSP...54.4311A. doi:10.1109/TSP.2006.881199. S2CID 7477309.
- ↑ Zha, Hongyuan; Ding, Chris; Gu, Ming; He, Xiaofeng; Simon, Horst D. (December 2001). "K के लिए वर्णक्रम संबंधी विश्राम - समूह का अर्थ है" (PDF). Neural Information Processing Systems Vol.14 (NIPS 2001): 1057–1064.
- ↑ Ding, Chris; He, Xiaofeng (July 2004). "K- साधन प्रमुख घटक विश्लेषण के माध्यम से समूह" (PDF). Proceedings of International Conference on Machine Learning (ICML 2004): 225–232.
- ↑ Drineas, Petros; Frieze, Alan M.; Kannan, Ravi; Vempala, Santosh; Vinay, Vishwanathan (2004). "एकवचन मूल्य अपघटन के माध्यम से बड़े रेखांकन को समूहित करना चाहिए।" (PDF). Machine Learning. 56 (1–3): 9–33. doi:10.1023/b:mach.0000033113.59016.96. S2CID 5892850. Retrieved 2012-08-02.
- ↑ Cohen, Michael B.; Elder, Sam; Musco, Cameron; Musco, Christopher; Persu, Madalina (2014). "K के लिए आयाम में अभाव - अर्थात समूहों और निम्न श्रेणी निकट (परिशिष्ट बी) है।". arXiv:1410.6801 [cs.DS].
- ↑ 24.0 24.1 Little, Max A.; Jones, Nick S. (2011). "Generalized Methods and Solvers for Piecewise Constant Signals: Part I" (PDF). Proceedings of the Royal Society A. 467 (2135): 3088–3114. Bibcode:2011RSPSA.467.3088L. doi:10.1098/rspa.2010.0671. PMC 3191861. PMID 22003312.
- ↑ Vinnikov, Alon; Shalev-Shwartz, Shai (2014). "K-माध्यिका आईसीए निस्पंदन को रिकवर करता है जब स्वतंत्र घटक विरल होते हैं" (PDF). Proceedings of the International Conference on Machine Learning (ICML 2014).
- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs named:12