केंद्रक (ज्यामितीय): Difference between revisions
No edit summary |
|||
| (21 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
{{short description|Mean ("average") position of all the points in a shape}} | {{short description|Mean ("average") position of all the points in a shape}} | ||
[[Image:Triangle.Centroid.svg|thumb|right|त्रिभुज का केन्द्रक]]गणित और भौतिकी में, समतल आकृति या ठोस आकृति का '''केन्द्रक''', जिसे ज्यामितीय केंद्र या आकृति केंद्र के रूप में भी जाना जाता है, आकृति की सतह के सभी बिंदुओं की अंकगणितीय औसत स्थिति है। यही परिभाषा ''n''-आयामी यूक्लिडियन समष्टि में किसी भी वस्तु तक फैली हुई है।<ref name = protter520>{{harvtxt|Protter|Morrey|1970|p=520}}</ref> | |||
[[Image:Triangle.Centroid.svg|thumb|right|त्रिभुज का केन्द्रक]]गणित और भौतिकी में, | [[ज्यामिति]] में, एक समान [[द्रव्यमान घनत्व]] को सामान्यतः माना जाता है, इस स्थिति में केन्द्रक या द्रव्यमान का केंद्र [[केन्द्रक]] के साथ मेल खाता है। अनौपचारिक रूप से, इसे उस बिंदु के रूप में समझा जा सकता है जिस पर आकार का एक कटआउट (समान रूप से वितरित द्रव्यमान के साथ) एक पिन की नोक पर पूरी तरह से संतुलित हो सकता है।<ref>{{harvtxt|Protter|Morrey|1970|p=521}}</ref> भौतिकी में, यदि [[गुरुत्वाकर्षण]] में भिन्नता पर विचार किया जाता है, तो गुरुत्वाकर्षण के केंद्र को उनके विशिष्ट [[भार]] द्वारा भारित सभी बिंदुओं के [[भारित माध्य]] के रूप में परिभाषित किया जा सकता है। | ||
[[ज्यामिति]] में, एक समान [[द्रव्यमान घनत्व]] को सामान्यतः माना जाता है, इस | |||
[[भूगोल]] में, पृथ्वी की सतह से समुद्र तल तक के एक क्षेत्र के रेडियल प्रक्षेपण का केन्द्रक क्षेत्र का [[भौगोलिक केंद्र]] है। | [[भूगोल]] में, पृथ्वी की सतह से समुद्र तल तक के एक क्षेत्र के रेडियल प्रक्षेपण का केन्द्रक क्षेत्र का [[भौगोलिक केंद्र]] है। | ||
== इतिहास == | == इतिहास == | ||
" | "केन्द्रक" शब्द हाल ही के सिक्के (1814) का है। इसका उपयोग गुरुत्वाकर्षण के केंद्र और द्रव्यमान के केंद्र के पुराने शब्दों के विकल्प के रूप में किया जाता है, जब उस बिंदु के विशुद्ध रूप से ज्यामितीय पहलुओं पर बल दिया जाता है। यह शब्द अंग्रेजी भाषा के लिए विशिष्ट है; फ्रेंच, उदाहरण के लिए, अधिकांश {{lang|fr|गुरुत्वाकर्षण का केंद्र}} का उपयोग करते हैं, और अन्य समान अर्थ वाले शब्दों का उपयोग करते हैं। | ||
गुरुत्वाकर्षण का केंद्र, जैसा कि नाम | गुरुत्वाकर्षण का केंद्र, जैसा कि नाम संकेत करता है, एक धारणा है जो यांत्रिकी में उत्पन्न हुई है, सबसे अधिक संभावना निर्माण गतिविधियों के संबंध में है। जब यह विचार पहली बार सामने आया तो यह अनिश्चित है, क्योंकि यह अवधारणा कई लोगों के साथ साधारण अंतर के साथ व्यक्तिगत रूप से घटित होने की संभावना है। पुरातनता में आंकड़ों के गुरुत्वाकर्षण के केंद्र का बड़े पैमाने पर अध्ययन किया गया था; [[चार्ल्स बोसुत]] ने [[आर्किमिडीज]] (287-212 ईसा पूर्व) को समतल के आंकड़ों के केन्द्रक को खोजने वाले पहले व्यक्ति होने का श्रेय दिया, चूँकि उन्होंने इसे कभी परिभाषित नहीं किया।<ref>{{Cite journal|last=Court|first=Nathan Altshiller|date=1960| title=केन्द्रक पर नोट्स|journal=The Mathematics Teacher|volume=53|issue=1|pages=33–35|doi=10.5951/MT.53.1.0033| jstor=27956057}}</ref> आर्किमिडीज द्वारा ठोस पदार्थों के केन्द्रक का उपचार खो गया है।<ref>{{Cite journal |last=Knorr |first=W. |date=1978 |title=ठोस पदार्थों के गुरुत्वाकर्षण के केंद्रों पर आर्किमिडीज का खोया हुआ ग्रंथ|url=https://doi.org/10.1007/BF03023072 |journal=The Mathematical Intelligencer |language=en |volume=1 |issue=2 |pages=102–109 |doi=10.1007/BF03023072 |issn=0343-6993}}</ref> | ||
यह संभावना नहीं है कि आर्किमिडीज ने [[यूक्लिड]] से सीधे एक बिंदु-त्रिभुज के गुरुत्वाकर्षण के केंद्र-में मिलने वाले प्रमेय को सीखा है, क्योंकि यह प्रस्ताव यूक्लिड के तत्वों में नहीं है। इस प्रस्ताव का पहला स्पष्ट | यह संभावना नहीं है कि आर्किमिडीज ने [[यूक्लिड]] से सीधे एक बिंदु-त्रिभुज के गुरुत्वाकर्षण के केंद्र-में मिलने वाले प्रमेय को सीखा है, क्योंकि यह प्रस्ताव यूक्लिड के तत्वों में नहीं है। इस प्रस्ताव का पहला स्पष्ट वर्णन [[अलेक्जेंड्रिया के हीरो]] (शायद पहली दशक सीई) के कारण है और उसके यांत्रिकी में होता है। यह जोड़ा जा सकता है कि उन्नीसवीं दशक तक समतल ज्यामिति पर पाठ्यपुस्तकों में प्रस्ताव सामान्य नहीं हुआ था। | ||
== गुण == | == गुण == | ||
[[उत्तल सेट]] वस्तु का ज्यामितीय केन्द्रक हमेशा वस्तु में स्थित होता है। एक गैर-उत्तल वस्तु में एक केंद्रक हो सकता है जो आकृति के बाहर ही हो। एक [[वलय (गणित)]] या एक [[कटोरा (बर्तन)]] का केंद्र, उदाहरण के लिए, वस्तु के केंद्रीय शून्य में स्थित होता है। | [[उत्तल सेट|उत्तल समुच्य]] वस्तु का ज्यामितीय केन्द्रक हमेशा वस्तु में स्थित होता है। एक गैर-उत्तल वस्तु में एक केंद्रक हो सकता है जो आकृति के बाहर ही हो। एक [[वलय (गणित)]] या एक [[कटोरा (बर्तन)]] का केंद्र, उदाहरण के लिए, वस्तु के केंद्रीय शून्य में स्थित होता है। | ||
यदि केन्द्रक परिभाषित है, तो यह [[समरूपता]] समूह में सभी आइसोमेट्री का एक निश्चित बिंदु है। विशेष रूप से, किसी वस्तु का ज्यामितीय केन्द्रक समरूपता के उसके सभी [[hyperplane|हाइपरप्लेन]] के प्रतिच्छेदन में स्थित होता है। कई आकृतियों ([[नियमित बहुभुज]],, नियमित | यदि केन्द्रक परिभाषित है, तो यह [[समरूपता]] समूह में सभी आइसोमेट्री का एक निश्चित बिंदु है। विशेष रूप से, किसी वस्तु का ज्यामितीय केन्द्रक समरूपता के उसके सभी [[hyperplane|हाइपरप्लेन]] के प्रतिच्छेदन में स्थित होता है। कई आकृतियों ([[नियमित बहुभुज]],, नियमित बहुतल, बेलन, [[आयत]], समचतुर्भुज, वृत्त, गोला, दीर्घवृत्त, [[दीर्घवृत्ताभ]], उत्तम दीर्घवृत्त, आदि) का केन्द्रक अकेले इस सिद्धांत द्वारा निर्धारित किया जा सकता है। | ||
विशेष रूप से, समांतर चतुर्भुज का केन्द्रक इसके दो [[विकर्ण|विकर्णों]] का मिलन बिंदु होता है। यह अन्य चतुर्भुजों के लिए सत्य नहीं है। | विशेष रूप से, समांतर चतुर्भुज का केन्द्रक इसके दो [[विकर्ण|विकर्णों]] का मिलन बिंदु होता है। यह अन्य चतुर्भुजों के लिए सत्य नहीं है। | ||
इसी कारण से, [[अनुवादकीय समरूपता]] के साथ एक वस्तु का केन्द्रक अपरिभाषित है (या संलग्न | इसी कारण से, [[अनुवादकीय समरूपता]] के साथ एक वस्तु का केन्द्रक अपरिभाषित है (या संलग्न समष्टि के बाहर स्थित है), क्योंकि एक अनुवाद का कोई निश्चित बिंदु नहीं है। | ||
== उदाहरण == | == उदाहरण == | ||
त्रिभुज का केन्द्रक त्रिभुज की तीन माध्यिकाओं का प्रतिच्छेदन होता है (प्रत्येक माध्यिका एक शीर्ष को विपरीत भुजा के मध्यबिंदु से जोड़ती है)।<ref name = altshiller66>{{harvtxt|Altshiller-Court|1925|p=66}}</ref> | त्रिभुज का केन्द्रक त्रिभुज की तीन माध्यिकाओं का प्रतिच्छेदन होता है (प्रत्येक माध्यिका एक शीर्ष को विपरीत भुजा के मध्यबिंदु से जोड़ती है)। त्रिभुज के केन्द्रक के अन्य गुणों के लिए, नीचे देखें।<ref name="altshiller66">{{harvtxt|Altshiller-Court|1925|p=66}}</ref> | ||
== | == स्थल निर्देशक == | ||
=== साहुल रेखा विधि === | === साहुल रेखा विधि === | ||
समान रूप से सघन | समान रूप से सघन योजनाकर्ता [[तलीय लामिना|तलीय पटल]] का केन्द्रक, जैसा कि नीचे चित्र (a) में है, समान आकार वाले समान घनत्व वाले पतले पिंड के द्रव्यमान के सहस्थित केंद्र को खोजने के लिए एक [[साहुल सूत्र # दीवार की सीध आंकने के लिए राजगीर का आला|साहुल सूत्र दीवार की सीध आंकने के लिए राजगीर का आला]] का उपयोग करके प्रयोगात्मक रूप से निर्धारित किया जा सकता है। शरीर को पिन द्वारा पकड़ा जाता है, एक बिंदु पर डाला जाता है, प्रकल्पित केन्द्रक से इस प्रकार से कि यह पिन के चारों ओर स्वतंत्र रूप से घूम सके; साहुल रेखा फिर पिन से गिरा दी जाती है (चित्र b)। साहुल सूत्र दीवार की सीध आंकने के लिए राजगीर का आला की स्थिति को सतह का मापन किया जाता है, और इस प्रक्रिया को वस्तु के केन्द्रक से भिन्न किसी भी बिंदु पर डाले गए पिन के साथ दोहराया जाता है। इन रेखाओं का अद्वितीय प्रतिच्छेदन बिंदु केन्द्रक होगा (चित्र c)। बशर्ते कि शरीर एक समान घनत्व का हो, इस तरह से बनी सभी रेखाओं में केन्द्रक सम्मलित होगा, और सभी रेखाएँ ठीक उसी समष्टि पर पार करेंगी। | ||
{| cellpadding=3 | {| cellpadding=3 | ||
| Line 39: | Line 38: | ||
| align=center | (c) | | align=center | (c) | ||
|} | |} | ||
इस विधि को (सिद्धांत रूप में) अवतल आकृतियों में विस्तारित किया जा सकता है जहां केन्द्रक आकृति के बाहर स्थित हो सकता है, और वस्तुतः ठोस (फिर से, एकसमान घनत्व का), जहां केन्द्रक शरीर के भीतर स्थित हो सकता है। | इस विधि को (सिद्धांत रूप में) अवतल आकृतियों में विस्तारित किया जा सकता है जहां केन्द्रक आकृति के बाहर स्थित हो सकता है, और वस्तुतः ठोस (फिर से, एकसमान घनत्व का), जहां केन्द्रक शरीर के भीतर स्थित हो सकता है। साहुल लाइनों की (आभासी) स्थिति को आकार के साथ खींचने के अलावा अन्य माध्यमों से अभिलेख करने की आवश्यकता है। | ||
=== संतुलन विधि === | === संतुलन विधि === | ||
उत्तल द्वि-आयामी आकृतियों के लिए, एक छोटे | उत्तल द्वि-आयामी आकृतियों के लिए, एक छोटे आकार को संतुलित करके केन्द्रक पाया जा सकता है, जैसे कि एक संकीर्ण सिलेंडर के ऊपर है। केन्द्रक दो आकृतियों के बीच संपर्क की सीमा के भीतर कहीं होता है (और ठीक उस बिंदु पर जहां आकृति एक पिन पर संतुलन बनाएगी)। सिद्धांत रूप में, उत्तरोत्तर संकरे सिलिंडरों का उपयोग मनमाना परिशुद्धता के लिए केन्द्रक को खोजने के लिए किया जा सकता है। व्यवहार में वायु धाराएँ इसे अव्यवहारिक बनाती हैं। चूंकि, कई बैलेंस से ओवरलैप श्रेणी को चिह्नित करके, शुद्धता का अधिक स्तर प्राप्त किया जा सकता है। | ||
=== अंक के एक परिमित | === अंक के एक परिमित समुच्चय की === | ||
<math>k</math> अंक <math>\mathbf{x}_1,\mathbf{x}_2,\ldots,\mathbf{x}_k</math> के परिमित समुच्चय का केन्द्रक <math>\R^n</math> में है<ref name = protter520/> | <math>k</math> अंक <math>\mathbf{x}_1,\mathbf{x}_2,\ldots,\mathbf{x}_k</math> के परिमित समुच्चय का केन्द्रक <math>\R^n</math> में है<ref name = protter520/> | ||
<math display="block">\mathbf{C} = \frac{\mathbf{x}_1 + \mathbf{x}_2 + \cdots + \mathbf{x}_k}{k} .</math> | <math display="block">\mathbf{C} = \frac{\mathbf{x}_1 + \mathbf{x}_2 + \cdots + \mathbf{x}_k}{k} .</math> | ||
यह बिंदु | यह बिंदु समुच्चय में स्वयं और प्रत्येक बिंदु के बीच वर्गित यूक्लिडियन दूरी के योग को कम करता है। | ||
=== ज्यामितीय अपघटन द्वारा === | === ज्यामितीय अपघटन द्वारा === | ||
एक समतल | एक समतल <math>X</math> के केन्द्रक की गणना इसे सरल आकृतियों की सीमित संख्या में विभाजित करके की जा सकती है <math>X_1, X_2, \dots, X_n</math>, प्रत्येक भाग के केन्द्रक <math>C_i</math> और क्षेत्रफल <math>A_i</math> की गणना करना, और फिर गणना करना | ||
<math display="block"> C_x = \frac{\sum_i {C_i}_x A_i}{\sum_i A_i} , C_y = \frac{\sum_i {C_i}_y A_i}{\sum_i A_i}</math> | <math display="block"> C_x = \frac{\sum_i {C_i}_x A_i}{\sum_i A_i} , C_y = \frac{\sum_i {C_i}_y A_i}{\sum_i A_i}</math> | ||
आकृति में छेद <math>X</math>, भागों के बीच ओवरलैप, या भाग जो आंकड़े के बाहर विस्तारित होते हैं, सभी को | आकृति में छेद <math>X</math>, भागों के बीच ओवरलैप, या भाग जो आंकड़े के बाहर विस्तारित होते हैं, सभी को ऋणात्मक क्षेत्रों <math>A_i</math> का उपयोग करके नियंत्रित किया जा सकता है . अर्थात् उपाय <math>A_i</math> को धनात्मक और ऋणात्मक संकेतों के साथ इस तरह से लिया जाना चाहिए कि कि सभी भागों के लिए <math>A_i</math> के संकेतों का योग जो किसी दिए गए बिंदु को संलग्न करता है <math>p</math> 1 है यदि <math>p</math> <math>X</math> से संबंधित है, और 0 अन्यथा। | ||
उदाहरण के लिए, नीचे दी गई आकृति ( | उदाहरण के लिए, नीचे दी गई आकृति (a) आसानी से एक वर्ग और एक त्रिकोण में विभाजित है, दोनों धनात्मक क्षेत्र के साथ; और एक गोलाकार छेद, ऋणात्मक क्षेत्र (b) के साथ। | ||
{{multiple images | {{multiple images | ||
|align= | |align=केंद्र | ||
|height=200 | |height=200 | ||
|direction= | |direction=क्षैतिज | ||
|image1=COG 1.png | |image1=COG 1.png | ||
|caption1=(a) 2D | |caption1=(a) 2D वस्तु | ||
|image2=COG 2.png | |image2=COG 2.png | ||
|caption2=(b) | |caption2=(b) सरल तत्वों का उपयोग करके वर्णित वस्तु | ||
|image3=COG 3.png | |image3=COG 3.png | ||
|caption3=(c) | |caption3=(c)वस्तु के तत्वों का केन्द्रक | ||
}} | }} | ||
प्रत्येक भाग का केन्द्रक केन्द्रक (c) की किसी भी सूची में पाया जा सकता है। फिर आकृति का केन्द्रक तीन बिंदुओं का भारित औसत है। आकृति के बाएँ किनारे से केंद्रक की क्षैतिज स्थिति है | प्रत्येक भाग का केन्द्रक केन्द्रक (c) की किसी भी सूची में पाया जा सकता है। फिर आकृति का केन्द्रक तीन बिंदुओं का भारित औसत है। आकृति के बाएँ किनारे से केंद्रक की क्षैतिज स्थिति है | ||
| Line 70: | Line 69: | ||
केन्द्रक की ऊर्ध्वाधर स्थिति इसी प्रकार पाई जाती है। | केन्द्रक की ऊर्ध्वाधर स्थिति इसी प्रकार पाई जाती है। | ||
किसी भी त्रि-आयामी वस्तु के लिए समान सूत्र लागू होता है, अतिरिक्त इसके कि प्रत्येक <math>A_i</math> का आयतन <math>X_i</math> होना चाहिए, न कि उसका क्षेत्रफल। यह <math>\R^d</math>के किसी भी उपसमुच्चय के लिए, किसी भी आयाम के लिए <math>d</math> द्वारा प्रतिस्थापित क्षेत्रों के साथ भागों के डी-आयामी उपाय। | |||
=== अभिन्न सूत्र द्वारा === | === अभिन्न सूत्र द्वारा === | ||
<math>\R^n</math> के उपसमुच्चय X के केन्द्रक की गणना समाकल द्वारा भी की जा सकती है | |||
<math display="block">C = \frac{\int x g(x) \; dx}{\int g(x) \; dx}</math> | <math display="block">C = \frac{\int x g(x) \; dx}{\int g(x) \; dx}</math> | ||
जहां | जहां अभिन्न को पूरे समष्टि पर ले जाया जाता है <math>\R^n</math>, और g उपसमुच्चय का संकेतक कार्य है, जो X के अंदर 1 और बाहर 0 है यह ।<ref name = protter526>{{harvtxt|Protter|Morrey|1970|p=526}}</ref> ध्यान दें कि भाजक X का माप है।यह सूत्र लागू नहीं किया जा सकता है यदि समुच्चय X का माप शून्य है, या यदि कोई अभिन्न विचलन है। | ||
केन्द्रक के लिए एक अन्य सूत्र है | केन्द्रक के लिए एक अन्य सूत्र है<math display="block">C_k = \frac{\int z S_k(z) \; dz}{\int g(x) \; dx}</math> | ||
<math display="block">C_k = \frac{\int z S_k(z) \; dz}{\int g(x) \; dx}</math> | जहां C<sub>''k''</sub> C, और S का kवाँ निर्देशांक है ''S<sub>k</sub>''(''z'') समीकरण x द्वारा परिभाषित हाइपरप्लेन के साथ X के प्रतिच्छेदन का माप है ''x<sub>k</sub>'' = ''z''। फिर से, भाजक केवल X का माप है। | ||
जहां | |||
समतल आकृति के लिए, विशेष रूप से, बेरिकेंटर निर्देशांक होते हैं | |||
<math display="block">C_{\mathrm x} = \frac{\int x S_{\mathrm y}(x) \; dx}{A}</math> | <math display="block">C_{\mathrm x} = \frac{\int x S_{\mathrm y}(x) \; dx}{A}</math><math display="block">C_{\mathrm y} = \frac{\int y S_{\mathrm x}(y) \; dy}{A}</math> | ||
<math display="block">C_{\mathrm y} = \frac{\int y S_{\mathrm x}(y) \; dy}{A}</math> | जहाँ A आकृति X का क्षेत्रफल है; ''S''<sub>y</sub>(''x'') एब्सिसा ''X'' पर लंबवत रेखा के साथ ''x'' के प्रतिच्छेदन की लंबाई है; और ''S''<sub>x</sub>(''y'') विनिमय वाले अक्षों के लिए समरूप मात्रा है। | ||
जहाँ A आकृति X का क्षेत्रफल है; | |||
=== एक परिबद्ध क्षेत्र का === | === एक परिबद्ध क्षेत्र का === | ||
केन्द्रक <math>(\bar{x},\;\bar{y})</math> [[निरंतर कार्य]] | केन्द्रक <math>(\bar{x},\;\bar{y})</math> एक क्षेत्र से घिरा हुआ है [[निरंतर कार्य|निरंतर कार्यों]] के ग्राफ़ <math>f</math> तथा <math>g</math> ऐसे कि <math>f(x) \geq g(x)</math> अंतराल पर <math>[a, b]</math> <math>a \leq x \leq b</math> दिया गया है <ref name="protter526" /><ref>{{harvtxt|Protter|Morrey|1970|p=527}}</ref> | ||
<math display="block">\bar{x}=\frac{1}{A}\int_a^b x[f(x) - g(x)]\;dx</math> | <math display="block">\bar{x}=\frac{1}{A}\int_a^b x[f(x) - g(x)]\;dx</math> | ||
<math display="block">\bar{y}=\frac{1}{A}\int_a^b \left[\frac{f(x) + g(x)}{2}\right][f(x) - g(x)]\;dx,</math> | <math display="block">\bar{y}=\frac{1}{A}\int_a^b \left[\frac{f(x) + g(x)}{2}\right][f(x) - g(x)]\;dx,</math> | ||
जहां <math>A</math> क्षेत्र का क्षेत्रफल है <math display="inline">\int_a^b \left[f(x) - g(x)\right] dx</math> द्वारा दिया गया) .<ref>{{harvtxt|Protter|Morrey|1970|p=528}}</ref><ref>{{harvtxt|Larson|1998|pp=458–460}}</ref> | |||
=== | === इंटरग्राफ के साथ === | ||
स्मूथ (या टुकड़े की तरह स्मूथ ) सीमा के साथ अनियमित आकार की वस्तु के केन्द्रक को खोजने के लिए एक पूर्णांक ([[प्लैनीमीटर]] का एक रिश्तेदार) का उपयोग किया जा सकता है। सम्मिलित गणितीय सिद्धांत ग्रीन प्रमेय का एक विशेष स्थिति है।<ref>{{harvtxt|Sangwin}}</ref> | |||
=== | === L-आकार की वस्तु का === | ||
यह | यह L-आकार की वस्तु के केन्द्रक को निर्धारित करने की एक विधि है। | ||
[[Image:CoG of L shape.svg|300px]] | [[Image:CoG of L shape.svg|300px]] आकृति को दो आयतों में विभाजित करें, जैसा कि चित्र 2 में दिखाया गया है। विकर्णों को खींचकर इन दो आयतों के केन्द्रक का पता लगाएं। केन्द्रक को मिलाने वाली एक रेखा खींचिए। आकृति का केन्द्रक इस रेखा AB पर स्थित होना चाहिए। | ||
# आकृति को दो अन्य आयतों में विभाजित करें, जैसा कि चित्र 3 में दिखाया गया है। विकर्णों को खींचकर इन दो आयतों के केन्द्रक का पता लगाएं। केन्द्रक को मिलाने वाली एक रेखा खींचिए। L-आकृति का केन्द्रक इस रेखा CD पर स्थित होना चाहिए। | # आकृति को दो अन्य आयतों में विभाजित करें, जैसा कि चित्र 3 में दिखाया गया है। विकर्णों को खींचकर इन दो आयतों के केन्द्रक का पता लगाएं। केन्द्रक को मिलाने वाली एक रेखा खींचिए। L-आकृति का केन्द्रक इस रेखा CD पर स्थित होना चाहिए। | ||
# चूँकि आकृति का केन्द्रक AB के साथ-साथ CD के साथ भी स्थित होना चाहिए, यह O पर इन दो रेखाओं के प्रतिच्छेदन पर होना चाहिए। बिंदु O, L-आकार की वस्तु के अंदर या बाहर स्थित हो सकता है। | # चूँकि आकृति का केन्द्रक AB के साथ-साथ CD के साथ भी स्थित होना चाहिए, यह O पर इन दो रेखाओं के प्रतिच्छेदन पर होना चाहिए। बिंदु O, L-आकार की वस्तु के अंदर या बाहर स्थित हो सकता है। | ||
| Line 111: | Line 108: | ||
| [[Image:Triangle centroid 1.svg]] [[Image:Triangle centroid 2.svg|200px]] | | [[Image:Triangle centroid 1.svg]] [[Image:Triangle centroid 2.svg|200px]] | ||
|} | |} | ||
त्रिभुज का केन्द्रक उसकी [[माध्यिका (ज्यामिति)]] का प्रतिच्छेदन बिंदु होता है (प्रत्येक शीर्ष को विपरीत भुजा के मध्यबिंदु से मिलाने वाली रेखा)।<ref name="altshiller66" /> केन्द्रक प्रत्येक माध्यिका को 2:1 के [[अनुपात]] में विभाजित करता है, जिसका अर्थ है कि यह प्रत्येक पक्ष से विपरीत शीर्ष तक की दूरी के ⅓ स्थित है (दाईं ओर आंकड़े देखें)।<ref>{{harvtxt |Altshiller-Court|1925|p=65}}</ref><ref>{{harvtxt|Kay|1969|p=184}}</ref> इसके [[कार्तीय निर्देशांक]] तीन शीर्षों के निर्देशांकों के अंकगणितीय माध्य हैं।यदि तीन कोने <math>L = (x_L, y_L),</math> <math>M= (x_M, y_M),</math> और <math>N= (x_N, y_N),</math> हैं तो केन्द्रक (यहाँ C को निरूपित किया जाता है लेकिन [[त्रिभुज ज्यामिति|त्रिभुज]] [[त्रिभुज ज्यामिति|ज्यामिति]] में G को सबसे सामान्य रूप से निरूपित किया जाता है)। <math display="block"> | |||
<math display="block"> | |||
C = \frac13(L+M+N) = \left(\frac{1}{3} (x_L+x_M+x_N),\;\; | C = \frac13(L+M+N) = \left(\frac{1}{3} (x_L+x_M+x_N),\;\; | ||
\frac{1}{3}(y_L+y_M+y_N)\right).</math> | \frac{1}{3}(y_L+y_M+y_N)\right).</math> | ||
त्रिरेखीय निर्देशांक में केन्द्रक को भुजाओं की लंबाई a, b, c और शीर्ष कोण L, M, N के संदर्भ में इनमें से किसी भी समतुल्य | |||
केन्द्रक इसलिए है <math>\tfrac13:\tfrac13:\tfrac13</math> बेरी केंद्रित निर्देशांक (गणित) में। | |||
त्रिरेखीय निर्देशांक में केन्द्रक को भुजाओं की लंबाई a, b, c और शीर्ष कोण L, M, N के संदर्भ में इनमें से किसी भी समतुल्य उपाय से व्यक्त किया जा सकता है:<ref>Clark Kimberling's Encyclopedia of Triangles {{cite web |url=http://faculty.evansville.edu/ck6/encyclopedia/ETC.html |title=Encyclopedia of Triangle Centers |access-date=2012-06-02 |url-status=dead |archive-url=https://web.archive.org/web/20120419171900/http://faculty.evansville.edu/ck6/encyclopedia/ETC.html |archive-date=2012-04-19 }}</ref> | |||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
C & =\frac{1}{a}:\frac{1}{b}:\frac{1}{c}=bc:ca:ab=\csc L :\csc M:\csc N \\[6pt] | C & =\frac{1}{a}:\frac{1}{b}:\frac{1}{c}=bc:ca:ab=\csc L :\csc M:\csc N \\[6pt] | ||
| Line 125: | Line 124: | ||
केन्द्रक द्रव्यमान का भौतिक केंद्र भी है यदि त्रिभुज सामग्री की एक समान शीट से बना है; या यदि सभी द्रव्यमान तीन शीर्षों पर केंद्रित हैं, और समान रूप से उनके बीच विभाजित हैं। दूसरी ओर, यदि द्रव्यमान को समान [[रैखिक घनत्व]] के साथ त्रिभुज की परिधि के साथ वितरित किया जाता है, तो द्रव्यमान का केंद्र [[स्पाइकर केंद्र]] (औसत दर्जे का त्रिभुज का केंद्र) पर स्थित होता है, जो कि (सामान्य रूप से) ज्यामितीय के साथ मेल नहीं खाता है। पूर्ण त्रिभुज का केंद्र। | केन्द्रक द्रव्यमान का भौतिक केंद्र भी है यदि त्रिभुज सामग्री की एक समान शीट से बना है; या यदि सभी द्रव्यमान तीन शीर्षों पर केंद्रित हैं, और समान रूप से उनके बीच विभाजित हैं। दूसरी ओर, यदि द्रव्यमान को समान [[रैखिक घनत्व]] के साथ त्रिभुज की परिधि के साथ वितरित किया जाता है, तो द्रव्यमान का केंद्र [[स्पाइकर केंद्र]] (औसत दर्जे का त्रिभुज का केंद्र) पर स्थित होता है, जो कि (सामान्य रूप से) ज्यामितीय के साथ मेल नहीं खाता है। पूर्ण त्रिभुज का केंद्र। | ||
त्रिभुज का क्षेत्रफल किसी भी भुजा की लंबाई का 1.5 गुणा भुजा से केंद्रक की लम्बवत दूरी का होता है।<ref>{{harvtxt|Johnson|2007|p=173}}</ref> | त्रिभुज का क्षेत्रफल किसी भी भुजा की लंबाई का 1.5 गुणा भुजा से केंद्रक की लम्बवत दूरी का होता है।<ref>{{harvtxt|Johnson|2007|p=173}}</ref> एक त्रिभुज का केन्द्रक इसके लंबकेन्द्र H और इसके परिकेन्द्र O के बीच इसकी यूलर रेखा पर स्थित होता है, जो पूर्व की तुलना में बाद वाले के बिल्कुल दुगुने निकट होता है:<ref>{{harvtxt|Altshiller-Court|1925|p=101}}</ref><ref>{{harvtxt|Kay|1969|pp=18,189,225–226}}</ref> | ||
एक त्रिभुज का केन्द्रक इसके लंबकेन्द्र H और इसके परिकेन्द्र O के बीच इसकी यूलर रेखा पर स्थित होता है, जो पूर्व की तुलना में बाद वाले के बिल्कुल दुगुने निकट होता है:<ref>{{harvtxt|Altshiller-Court|1925|p=101}}</ref><ref>{{harvtxt|Kay|1969|pp=18,189,225–226}}</ref> | |||
<math display="block">\overline{CH}=2\overline{CO}.</math> | <math display="block">\overline{CH}=2\overline{CO}.</math> | ||
इसके | इसके अतिरिक्त, केंद्र I और [[नौ-बिंदु केंद्र]] N के लिए, हमारे पास है | ||
<math display="block">\begin{align} | <math display="block">\begin{align} | ||
\overline{CH} &=4\overline{CN} \\[5pt] | \overline{CH} &=4\overline{CN} \\[5pt] | ||
| Line 141: | Line 139: | ||
एक त्रिभुज के केन्द्रक का समकोणीय संयुग्म इसका सममध्यक है। | एक त्रिभुज के केन्द्रक का समकोणीय संयुग्म इसका सममध्यक है। | ||
केन्द्रक से गुजरने वाली तीन माध्यिकाओं में से कोई भी त्रिभुज के क्षेत्रफल को आधे में विभाजित करती है। यह केन्द्रक के माध्यम से अन्य रेखाओं के लिए सत्य नहीं है; समान-क्षेत्र विभाजन से सबसे बड़ा | केन्द्रक से गुजरने वाली तीन माध्यिकाओं में से कोई भी त्रिभुज के क्षेत्रफल को आधे में विभाजित करती है। यह केन्द्रक के माध्यम से अन्य रेखाओं के लिए सत्य नहीं है; समान-क्षेत्र विभाजन से सबसे बड़ा प्रसमष्टि तब होता है जब केन्द्रक के माध्यम से एक रेखा त्रिकोण के किनारे के समानांतर होती है, जिससे एक छोटा त्रिकोण और एक समलम्ब बनता है; इस सम्बन्ध में [[समलम्ब]] का क्षेत्रफल मूल त्रिभुज का 5/9 है।<ref name=Bottomley2002>{{cite web|last=Bottomley|first=Henry|title=त्रिभुज की माध्यिकाएँ और क्षेत्रफल द्विभाजक| url=http://www.se16.info/js/halfarea.htm|access-date=27 September 2013}}</ref> मान लीजिए कि P त्रिभुज के समतल में कोई बिंदु है, जिसके शीर्ष A, B, और C और केन्द्रक G हैं। फिर तीन शीर्षों से P की वर्ग दूरियों का योग शीर्षों से केंद्रक G की वर्ग दूरी के योग से अधिक है। P और G के बीच की दूरी के वर्ग के तीन गुना से:<ref name = altshiller70>{{harvtxt|Altshiller-Court|1925|pp=70–71}}</ref> | ||
मान लीजिए कि P त्रिभुज के समतल में कोई बिंदु है, जिसके शीर्ष A, B, और C और केन्द्रक G हैं। फिर तीन शीर्षों से P की वर्ग दूरियों का योग शीर्षों से केंद्रक G की वर्ग दूरी के योग से अधिक है। P और G के बीच की दूरी के वर्ग के तीन गुना से:<ref name = altshiller70>{{harvtxt|Altshiller-Court|1925|pp=70–71}}</ref> | |||
<math display="block">PA^2+PB^2+PC^2=GA^2+GB^2+GC^2+3PG^2.</math> | <math display="block">PA^2+PB^2+PC^2=GA^2+GB^2+GC^2+3PG^2.</math> | ||
त्रिभुज की भुजाओं के वर्गों का योग शीर्षों से केन्द्रक की वर्ग दूरी के योग के तीन गुना के बराबर होता है:<ref name = altshiller70/> | त्रिभुज की भुजाओं के वर्गों का योग शीर्षों से केन्द्रक की वर्ग दूरी के योग के तीन गुना के बराबर होता है:<ref name = altshiller70/> | ||
<math display="block">AB^2+BC^2+CA^2=3(GA^2+GB^2+GC^2).</math> | <math display="block">AB^2+BC^2+CA^2=3(GA^2+GB^2+GC^2).</math> | ||
एक त्रिभुज का केन्द्रक वह बिंदु है जो त्रिभुज की पार्श्व रेखाओं से किसी बिंदु की निर्देशित दूरियों के गुणनफल को अधिकतम करता है।<ref>{{cite journal|first =Clark|last= Kimberling|title=सममध्य बिंदु, केन्द्रक और अन्य त्रिभुज केंद्रों के लिए त्रिरेखीय दूरी असमानताएँ|journal =Forum Geometricorum|volume= 10|date=201|pages = 135–139|url = http://forumgeom.fau.edu/FG2010volume10/FG201015index.html }}</ref> | एक त्रिभुज का केन्द्रक वह बिंदु है जो त्रिभुज की पार्श्व रेखाओं से किसी बिंदु की निर्देशित दूरियों के गुणनफल को अधिकतम करता है।<ref>{{cite journal|first =Clark|last= Kimberling|title=सममध्य बिंदु, केन्द्रक और अन्य त्रिभुज केंद्रों के लिए त्रिरेखीय दूरी असमानताएँ|journal =Forum Geometricorum|volume= 10|date=201|pages = 135–139|url = http://forumgeom.fau.edu/FG2010volume10/FG201015index.html }}</ref> मान लीजिए ABC एक त्रिभुज है, मान लीजिए G इसका केंद्रक है, और मान लीजिए D, E, और F क्रमशः BC, CA और AB के मध्य बिंदु हैं। ABC के विमान में किसी भी बिंदु P के लिए<ref>Gerald A. Edgar, Daniel H. Ullman & Douglas B. West (2018) Problems and Solutions, The American Mathematical Monthly, 125:1, 81-89, DOI: 10.1080/00029890.2018.1397465</ref> | ||
मान लीजिए ABC एक त्रिभुज है, मान लीजिए G इसका केंद्रक है, और मान लीजिए D, E, और F क्रमशः BC, CA और AB के मध्य बिंदु हैं। | |||
=== एक [[बहुभुज]] का === | === एक [[बहुभुज]] का === | ||
एक गैर-स्व-प्रतिच्छेदित बंद बहुभुज का केन्द्रक n शीर्षों द्वारा परिभाषित (x<sub>0</sub>, | एक गैर-स्व-प्रतिच्छेदित बंद बहुभुज का केन्द्रक n शीर्षों द्वारा परिभाषित ((''x''<sub>0</sub>,''y''<sub>0</sub>)), (''x''<sub>1</sub>,''y''<sub>1</sub>), ..., (''x<sub>n</sub>''<sub>−1</sub>,''y<sub>n</sub>''<sub>−1</sub>) बिंदु है (''C''<sub>x</sub>, ''C''<sub>y</sub>),<ref name=":0" /> जहाँ | ||
<math display="block">C_{\mathrm x} = \frac{1}{6A}\sum_{i=0}^{n-1}(x_i+x_{i+1})(x_i\ y_{i+1} - x_{i+1}\ y_i),</math> तथा | <math display="block">C_{\mathrm x} = \frac{1}{6A}\sum_{i=0}^{n-1}(x_i+x_{i+1})(x_i\ y_{i+1} - x_{i+1}\ y_i),</math> तथा | ||
<math display="block">C_{\mathrm y} = \frac{1}{6A}\sum_{i=0}^{n-1}(y_i+y_{i+1})(x_i\ y_{i+1} - x_{i+1}\ y_i),</math> | <math display="block">C_{\mathrm y} = \frac{1}{6A}\sum_{i=0}^{n-1}(y_i+y_{i+1})(x_i\ y_{i+1} - x_{i+1}\ y_i),</math> | ||
और जहाँ A बहुभुज का हस्ताक्षरित क्षेत्र है,<ref name=":0">{{harvtxt|Bourke|1997}}</ref> जैसा कि फावड़ा सूत्र द्वारा वर्णित है: | और जहाँ A बहुभुज का हस्ताक्षरित क्षेत्र है,<ref name=":0">{{harvtxt|Bourke|1997}}</ref> जैसा कि फावड़ा सूत्र द्वारा वर्णित है: | ||
<math display="block">A = \frac{1}{2}\sum_{i=0}^{n-1} (x_i\ y_{i+1} - x_{i+1}\ y_i).</math> | <math display="block">A = \frac{1}{2}\sum_{i=0}^{n-1} (x_i\ y_{i+1} - x_{i+1}\ y_i).</math> | ||
इन सूत्रों में, शीर्षों को बहुभुज की परिधि के साथ उनकी घटना के क्रम में क्रमांकित माना जाता है; इसके | इन सूत्रों में, शीर्षों को बहुभुज की परिधि के साथ उनकी घटना के क्रम में क्रमांकित माना जाता है; इसके अतिरिक्त, शिखर( ''x<sub>n</sub>'', ''y<sub>n</sub>'' ) को (''x''<sub>0</sub>, ''y''<sub>0</sub>), अर्थ {{tmath|i + 1}} अंतिम स्थिति पर चारों ओर लूप होना चाहिए {{tmath|1=i = 0}}. (यदि अंक दक्षिणावर्त क्रम में गिने जाते हैं, तो क्षेत्र A, ऊपर के रूप में गणना की गई, ऋणात्मक होगी; चूंकि, केन्द्रक निर्देशांक इस स्थिति में भी सही होंगे।) | ||
=== एक शंकु या पिरामिड का === | === एक शंकु या पिरामिड का === | ||
[[शंकु (ज्यामिति)]] या [[पिरामिड (ज्यामिति)]] का केन्द्रक रेखा खंड पर स्थित होता है जो [[शीर्ष (ज्यामिति)]] को आधार के केन्द्रक से जोड़ता है। एक ठोस शंकु या पिरामिड के लिए, केन्द्रक आधार से शीर्ष तक की दूरी का 1/4 है। एक शंकु या पिरामिड के लिए जो बिना किसी आधार के सिर्फ एक खोल है, केन्द्रक आधार तल से शीर्ष तक की दूरी का 1/3 है। | |||
चतुष्फलक और n-आयामी सरल का एक [[चतुर्पाश्वीय]] त्रि-आयामी समष्टि में एक वस्तु है जिसके चेहरे (ज्यामिति) के रूप में चार त्रिकोण होते हैं। चतुष्फलक के शीर्ष को विपरीत फलक के केन्द्रक से मिलाने वाले रेखाखंड को माध्यिका कहते हैं और दो विपरीत किनारों के मध्यबिंदुओं को मिलाने वाले रेखाखंड को द्विमाध्यिका कहते हैं। अतः चार माध्यिकाएँ और तीन द्विमाध्यिकाएँ हैं। ये सात रेखाखंड चतुष्फलक के केन्द्रक पर मिलते हैं।<ref>Leung, Kam-tim; and Suen, Suk-nam; "Vectors, matrices and geometry", Hong Kong University Press, 1994, pp. 53–54</ref> माध्यिकाओं को केन्द्रक द्वारा 3:1 के अनुपात में विभाजित किया जाता है। एक चतुष्फलक का केन्द्रक इसके मोंज बिंदु और परिकेंद्र (परिवृत्त क्षेत्र का केंद्र) के बीच का मध्य बिंदु है। ये तीन बिंदु चतुष्फलक की यूलर रेखा को परिभाषित करते हैं जो त्रिभुज की यूलर रेखा के समान है। | |||
एक [[चतुर्पाश्वीय]] त्रि-आयामी | |||
ये परिणाम निम्नलिखित तरीके से किसी भी एन-डायमेंशनल [[सिंप्लेक्स]] के लिए सामान्यीकृत होते हैं। यदि एक सिम्प्लेक्स के | ये परिणाम निम्नलिखित तरीके से किसी भी एन-डायमेंशनल [[सिंप्लेक्स]] के लिए सामान्यीकृत होते हैं। यदि एक सिम्प्लेक्स के ऊर्ध्वाधर का समुच्य <math>{v_0,\ldots,v_n}</math> है , तो शीर्षों को सदिश (ज्यामिति) मानते हुए, केन्द्रक है | ||
<math display="block">C = \frac{1}{n+1}\sum_{i=0}^n v_i.</math> | <math display="block">C = \frac{1}{n+1}\sum_{i=0}^n v_i.</math> | ||
ज्यामितीय केन्द्रक द्रव्यमान के केंद्र के साथ मेल खाता है यदि द्रव्यमान समान रूप से पूरे सिंप्लेक्स पर वितरित किया जाता है, या शिखर पर n+1 समान द्रव्यमान के रूप में केंद्रित होता है। | ज्यामितीय केन्द्रक द्रव्यमान के केंद्र के साथ मेल खाता है यदि द्रव्यमान समान रूप से पूरे सिंप्लेक्स पर वितरित किया जाता है, या शिखर पर n+1 समान द्रव्यमान के रूप में केंद्रित होता है। | ||
=== | === गोलार्द्ध === | ||
ठोस गोलार्द्ध का केन्द्रक (अर्थात एक ठोस गेंद का आधा) गोले के केंद्र को गोलार्द्ध के ध्रुव से 3:5 के अनुपात में जोड़ने वाले रेखा खंड को विभाजित करता है (अर्थात यह केंद्र से ध्रुव तक के रास्ते का 3/8 भाग है)।एक खोखले गोलार्ध का केन्द्रक (अर्थात एक खोखले गोले का आधा भाग) गोले के केंद्र को गोलार्ध के ध्रुव से जोड़ने वाले रेखा खंड को आधे हिस्से में विभाजित करता है। | |||
== यह भी देखें == | == यह भी देखें == | ||
* [[चेबिशेव केंद्र]] | * [[चेबिशेव केंद्र]] | ||
* वृत्ताकार माध्य | * वृत्ताकार माध्य | ||
* फ्रेचेट | * फ्रेचेट अर्थ | ||
* के- | * के-अर्थ एल्गोरिथम | के-अर्थ एल्गोरिथम | ||
* सेंट्रोइड्स की सूची | * सेंट्रोइड्स की सूची | ||
* [[द्रव्यमान के केंद्र का पता लगाना]] | * [[द्रव्यमान के केंद्र का पता लगाना]] | ||
| Line 197: | Line 189: | ||
* {{ citation | first1 = Murray H. | last1 = Protter | first2=Charles B. Jr. | last2=Morrey | year = 1970 | lccn = 76087042 | title = College Calculus with Analytic Geometry | edition = 2nd | publisher = [[Addison-Wesley]] | location = Reading }} | * {{ citation | first1 = Murray H. | last1 = Protter | first2=Charles B. Jr. | last2=Morrey | year = 1970 | lccn = 76087042 | title = College Calculus with Analytic Geometry | edition = 2nd | publisher = [[Addison-Wesley]] | location = Reading }} | ||
* {{ citation | first = C.J. | last = Sangwin | title = Locating the centre of mass by mechanical means | url = http://web.mat.bham.ac.uk/C.J.Sangwin/Publications/integrometer.pdf | url-status = dead | archive-url = https://web.archive.org/web/20131113082631/http://web.mat.bham.ac.uk/C.J.Sangwin/Publications/integrometer.pdf | archive-date = November 13, 2013}} | * {{ citation | first = C.J. | last = Sangwin | title = Locating the centre of mass by mechanical means | url = http://web.mat.bham.ac.uk/C.J.Sangwin/Publications/integrometer.pdf | url-status = dead | archive-url = https://web.archive.org/web/20131113082631/http://web.mat.bham.ac.uk/C.J.Sangwin/Publications/integrometer.pdf | archive-date = November 13, 2013}} | ||
== बाहरी संबंध == | == बाहरी संबंध == | ||
* {{Mathworld|id=GeometricCentroid|title=Geometric Centroid}} | * {{Mathworld|id=GeometricCentroid|title=Geometric Centroid}} | ||
| Line 250: | Line 195: | ||
* Interactive animations showing [http://www.mathopenref.com/trianglecentroid.html Centroid of a triangle] and [http://www.mathopenref.com/constcentroid.html Centroid construction with compass and straightedge] | * Interactive animations showing [http://www.mathopenref.com/trianglecentroid.html Centroid of a triangle] and [http://www.mathopenref.com/constcentroid.html Centroid construction with compass and straightedge] | ||
* [http://dynamicmathematicslearning.com/findingtrianglemedian.html Experimentally finding the medians and centroid of a triangle] at [http://dynamicmathematicslearning.com/JavaGSPLinks.htm Dynamic Geometry Sketches], an interactive dynamic geometry sketch using the gravity simulator of Cinderella. | * [http://dynamicmathematicslearning.com/findingtrianglemedian.html Experimentally finding the medians and centroid of a triangle] at [http://dynamicmathematicslearning.com/JavaGSPLinks.htm Dynamic Geometry Sketches], an interactive dynamic geometry sketch using the gravity simulator of Cinderella. | ||
[[Category:Articles containing French-language text]] | |||
[[Category:Articles with short description]] | |||
[[Category:CS1 English-language sources (en)]] | |||
[[Category:CS1 français-language sources (fr)]] | |||
[[Category:CS1 maint]] | |||
[[Category:CS1 Ελληνικά-language sources (el)]] | |||
[[Category:Citation Style 1 templates|W]] | |||
[[Category:Collapse templates]] | |||
[[Category:Created On 27/11/2022]] | |||
[[Category:Machine Translated Page]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates based on the Citation/CS1 Lua module]] | |||
[[Category:Templates generating COinS|Cite web]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates used by AutoWikiBrowser|Cite web]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikipedia fully protected templates|Cite web]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:एफ़िन ज्यामिति]] | [[Category:एफ़िन ज्यामिति]] | ||
[[Category:ज्यामितीय केंद्र]] | [[Category:ज्यामितीय केंद्र]] | ||
[[Category:त्रिकोण केंद्र]] | [[Category:त्रिकोण केंद्र]] | ||
[[Category:साधन]] | |||
[[Category: | |||
Latest revision as of 12:37, 27 October 2023
गणित और भौतिकी में, समतल आकृति या ठोस आकृति का केन्द्रक, जिसे ज्यामितीय केंद्र या आकृति केंद्र के रूप में भी जाना जाता है, आकृति की सतह के सभी बिंदुओं की अंकगणितीय औसत स्थिति है। यही परिभाषा n-आयामी यूक्लिडियन समष्टि में किसी भी वस्तु तक फैली हुई है।[1]
ज्यामिति में, एक समान द्रव्यमान घनत्व को सामान्यतः माना जाता है, इस स्थिति में केन्द्रक या द्रव्यमान का केंद्र केन्द्रक के साथ मेल खाता है। अनौपचारिक रूप से, इसे उस बिंदु के रूप में समझा जा सकता है जिस पर आकार का एक कटआउट (समान रूप से वितरित द्रव्यमान के साथ) एक पिन की नोक पर पूरी तरह से संतुलित हो सकता है।[2] भौतिकी में, यदि गुरुत्वाकर्षण में भिन्नता पर विचार किया जाता है, तो गुरुत्वाकर्षण के केंद्र को उनके विशिष्ट भार द्वारा भारित सभी बिंदुओं के भारित माध्य के रूप में परिभाषित किया जा सकता है।
भूगोल में, पृथ्वी की सतह से समुद्र तल तक के एक क्षेत्र के रेडियल प्रक्षेपण का केन्द्रक क्षेत्र का भौगोलिक केंद्र है।
इतिहास
"केन्द्रक" शब्द हाल ही के सिक्के (1814) का है। इसका उपयोग गुरुत्वाकर्षण के केंद्र और द्रव्यमान के केंद्र के पुराने शब्दों के विकल्प के रूप में किया जाता है, जब उस बिंदु के विशुद्ध रूप से ज्यामितीय पहलुओं पर बल दिया जाता है। यह शब्द अंग्रेजी भाषा के लिए विशिष्ट है; फ्रेंच, उदाहरण के लिए, अधिकांश गुरुत्वाकर्षण का केंद्र का उपयोग करते हैं, और अन्य समान अर्थ वाले शब्दों का उपयोग करते हैं।
गुरुत्वाकर्षण का केंद्र, जैसा कि नाम संकेत करता है, एक धारणा है जो यांत्रिकी में उत्पन्न हुई है, सबसे अधिक संभावना निर्माण गतिविधियों के संबंध में है। जब यह विचार पहली बार सामने आया तो यह अनिश्चित है, क्योंकि यह अवधारणा कई लोगों के साथ साधारण अंतर के साथ व्यक्तिगत रूप से घटित होने की संभावना है। पुरातनता में आंकड़ों के गुरुत्वाकर्षण के केंद्र का बड़े पैमाने पर अध्ययन किया गया था; चार्ल्स बोसुत ने आर्किमिडीज (287-212 ईसा पूर्व) को समतल के आंकड़ों के केन्द्रक को खोजने वाले पहले व्यक्ति होने का श्रेय दिया, चूँकि उन्होंने इसे कभी परिभाषित नहीं किया।[3] आर्किमिडीज द्वारा ठोस पदार्थों के केन्द्रक का उपचार खो गया है।[4] यह संभावना नहीं है कि आर्किमिडीज ने यूक्लिड से सीधे एक बिंदु-त्रिभुज के गुरुत्वाकर्षण के केंद्र-में मिलने वाले प्रमेय को सीखा है, क्योंकि यह प्रस्ताव यूक्लिड के तत्वों में नहीं है। इस प्रस्ताव का पहला स्पष्ट वर्णन अलेक्जेंड्रिया के हीरो (शायद पहली दशक सीई) के कारण है और उसके यांत्रिकी में होता है। यह जोड़ा जा सकता है कि उन्नीसवीं दशक तक समतल ज्यामिति पर पाठ्यपुस्तकों में प्रस्ताव सामान्य नहीं हुआ था।
गुण
उत्तल समुच्य वस्तु का ज्यामितीय केन्द्रक हमेशा वस्तु में स्थित होता है। एक गैर-उत्तल वस्तु में एक केंद्रक हो सकता है जो आकृति के बाहर ही हो। एक वलय (गणित) या एक कटोरा (बर्तन) का केंद्र, उदाहरण के लिए, वस्तु के केंद्रीय शून्य में स्थित होता है।
यदि केन्द्रक परिभाषित है, तो यह समरूपता समूह में सभी आइसोमेट्री का एक निश्चित बिंदु है। विशेष रूप से, किसी वस्तु का ज्यामितीय केन्द्रक समरूपता के उसके सभी हाइपरप्लेन के प्रतिच्छेदन में स्थित होता है। कई आकृतियों (नियमित बहुभुज,, नियमित बहुतल, बेलन, आयत, समचतुर्भुज, वृत्त, गोला, दीर्घवृत्त, दीर्घवृत्ताभ, उत्तम दीर्घवृत्त, आदि) का केन्द्रक अकेले इस सिद्धांत द्वारा निर्धारित किया जा सकता है।
विशेष रूप से, समांतर चतुर्भुज का केन्द्रक इसके दो विकर्णों का मिलन बिंदु होता है। यह अन्य चतुर्भुजों के लिए सत्य नहीं है।
इसी कारण से, अनुवादकीय समरूपता के साथ एक वस्तु का केन्द्रक अपरिभाषित है (या संलग्न समष्टि के बाहर स्थित है), क्योंकि एक अनुवाद का कोई निश्चित बिंदु नहीं है।
उदाहरण
त्रिभुज का केन्द्रक त्रिभुज की तीन माध्यिकाओं का प्रतिच्छेदन होता है (प्रत्येक माध्यिका एक शीर्ष को विपरीत भुजा के मध्यबिंदु से जोड़ती है)। त्रिभुज के केन्द्रक के अन्य गुणों के लिए, नीचे देखें।[5]
स्थल निर्देशक
साहुल रेखा विधि
समान रूप से सघन योजनाकर्ता तलीय पटल का केन्द्रक, जैसा कि नीचे चित्र (a) में है, समान आकार वाले समान घनत्व वाले पतले पिंड के द्रव्यमान के सहस्थित केंद्र को खोजने के लिए एक साहुल सूत्र दीवार की सीध आंकने के लिए राजगीर का आला का उपयोग करके प्रयोगात्मक रूप से निर्धारित किया जा सकता है। शरीर को पिन द्वारा पकड़ा जाता है, एक बिंदु पर डाला जाता है, प्रकल्पित केन्द्रक से इस प्रकार से कि यह पिन के चारों ओर स्वतंत्र रूप से घूम सके; साहुल रेखा फिर पिन से गिरा दी जाती है (चित्र b)। साहुल सूत्र दीवार की सीध आंकने के लिए राजगीर का आला की स्थिति को सतह का मापन किया जाता है, और इस प्रक्रिया को वस्तु के केन्द्रक से भिन्न किसी भी बिंदु पर डाले गए पिन के साथ दोहराया जाता है। इन रेखाओं का अद्वितीय प्रतिच्छेदन बिंदु केन्द्रक होगा (चित्र c)। बशर्ते कि शरीर एक समान घनत्व का हो, इस तरह से बनी सभी रेखाओं में केन्द्रक सम्मलित होगा, और सभी रेखाएँ ठीक उसी समष्टि पर पार करेंगी।
| (a) | (b) | (c) |
इस विधि को (सिद्धांत रूप में) अवतल आकृतियों में विस्तारित किया जा सकता है जहां केन्द्रक आकृति के बाहर स्थित हो सकता है, और वस्तुतः ठोस (फिर से, एकसमान घनत्व का), जहां केन्द्रक शरीर के भीतर स्थित हो सकता है। साहुल लाइनों की (आभासी) स्थिति को आकार के साथ खींचने के अलावा अन्य माध्यमों से अभिलेख करने की आवश्यकता है।
संतुलन विधि
उत्तल द्वि-आयामी आकृतियों के लिए, एक छोटे आकार को संतुलित करके केन्द्रक पाया जा सकता है, जैसे कि एक संकीर्ण सिलेंडर के ऊपर है। केन्द्रक दो आकृतियों के बीच संपर्क की सीमा के भीतर कहीं होता है (और ठीक उस बिंदु पर जहां आकृति एक पिन पर संतुलन बनाएगी)। सिद्धांत रूप में, उत्तरोत्तर संकरे सिलिंडरों का उपयोग मनमाना परिशुद्धता के लिए केन्द्रक को खोजने के लिए किया जा सकता है। व्यवहार में वायु धाराएँ इसे अव्यवहारिक बनाती हैं। चूंकि, कई बैलेंस से ओवरलैप श्रेणी को चिह्नित करके, शुद्धता का अधिक स्तर प्राप्त किया जा सकता है।
अंक के एक परिमित समुच्चय की
अंक के परिमित समुच्चय का केन्द्रक में है[1]
ज्यामितीय अपघटन द्वारा
एक समतल के केन्द्रक की गणना इसे सरल आकृतियों की सीमित संख्या में विभाजित करके की जा सकती है , प्रत्येक भाग के केन्द्रक और क्षेत्रफल की गणना करना, और फिर गणना करना
उदाहरण के लिए, नीचे दी गई आकृति (a) आसानी से एक वर्ग और एक त्रिकोण में विभाजित है, दोनों धनात्मक क्षेत्र के साथ; और एक गोलाकार छेद, ऋणात्मक क्षेत्र (b) के साथ।
प्रत्येक भाग का केन्द्रक केन्द्रक (c) की किसी भी सूची में पाया जा सकता है। फिर आकृति का केन्द्रक तीन बिंदुओं का भारित औसत है। आकृति के बाएँ किनारे से केंद्रक की क्षैतिज स्थिति है
किसी भी त्रि-आयामी वस्तु के लिए समान सूत्र लागू होता है, अतिरिक्त इसके कि प्रत्येक का आयतन होना चाहिए, न कि उसका क्षेत्रफल। यह के किसी भी उपसमुच्चय के लिए, किसी भी आयाम के लिए द्वारा प्रतिस्थापित क्षेत्रों के साथ भागों के डी-आयामी उपाय।
अभिन्न सूत्र द्वारा
के उपसमुच्चय X के केन्द्रक की गणना समाकल द्वारा भी की जा सकती है
केन्द्रक के लिए एक अन्य सूत्र है
समतल आकृति के लिए, विशेष रूप से, बेरिकेंटर निर्देशांक होते हैं
एक परिबद्ध क्षेत्र का
केन्द्रक एक क्षेत्र से घिरा हुआ है निरंतर कार्यों के ग्राफ़ तथा ऐसे कि अंतराल पर दिया गया है [6][7]
इंटरग्राफ के साथ
स्मूथ (या टुकड़े की तरह स्मूथ ) सीमा के साथ अनियमित आकार की वस्तु के केन्द्रक को खोजने के लिए एक पूर्णांक (प्लैनीमीटर का एक रिश्तेदार) का उपयोग किया जा सकता है। सम्मिलित गणितीय सिद्धांत ग्रीन प्रमेय का एक विशेष स्थिति है।[10]
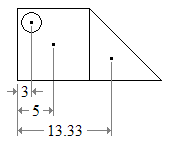
L-आकार की वस्तु का
यह L-आकार की वस्तु के केन्द्रक को निर्धारित करने की एक विधि है।
 आकृति को दो आयतों में विभाजित करें, जैसा कि चित्र 2 में दिखाया गया है। विकर्णों को खींचकर इन दो आयतों के केन्द्रक का पता लगाएं। केन्द्रक को मिलाने वाली एक रेखा खींचिए। आकृति का केन्द्रक इस रेखा AB पर स्थित होना चाहिए।
आकृति को दो आयतों में विभाजित करें, जैसा कि चित्र 2 में दिखाया गया है। विकर्णों को खींचकर इन दो आयतों के केन्द्रक का पता लगाएं। केन्द्रक को मिलाने वाली एक रेखा खींचिए। आकृति का केन्द्रक इस रेखा AB पर स्थित होना चाहिए।
- आकृति को दो अन्य आयतों में विभाजित करें, जैसा कि चित्र 3 में दिखाया गया है। विकर्णों को खींचकर इन दो आयतों के केन्द्रक का पता लगाएं। केन्द्रक को मिलाने वाली एक रेखा खींचिए। L-आकृति का केन्द्रक इस रेखा CD पर स्थित होना चाहिए।
- चूँकि आकृति का केन्द्रक AB के साथ-साथ CD के साथ भी स्थित होना चाहिए, यह O पर इन दो रेखाओं के प्रतिच्छेदन पर होना चाहिए। बिंदु O, L-आकार की वस्तु के अंदर या बाहर स्थित हो सकता है।
त्रिभुज का
 
|
त्रिभुज का केन्द्रक उसकी माध्यिका (ज्यामिति) का प्रतिच्छेदन बिंदु होता है (प्रत्येक शीर्ष को विपरीत भुजा के मध्यबिंदु से मिलाने वाली रेखा)।[5] केन्द्रक प्रत्येक माध्यिका को 2:1 के अनुपात में विभाजित करता है, जिसका अर्थ है कि यह प्रत्येक पक्ष से विपरीत शीर्ष तक की दूरी के ⅓ स्थित है (दाईं ओर आंकड़े देखें)।[11][12] इसके कार्तीय निर्देशांक तीन शीर्षों के निर्देशांकों के अंकगणितीय माध्य हैं।यदि तीन कोने और हैं तो केन्द्रक (यहाँ C को निरूपित किया जाता है लेकिन त्रिभुज ज्यामिति में G को सबसे सामान्य रूप से निरूपित किया जाता है)।
केन्द्रक इसलिए है बेरी केंद्रित निर्देशांक (गणित) में।
त्रिरेखीय निर्देशांक में केन्द्रक को भुजाओं की लंबाई a, b, c और शीर्ष कोण L, M, N के संदर्भ में इनमें से किसी भी समतुल्य उपाय से व्यक्त किया जा सकता है:[13]
त्रिभुज का क्षेत्रफल किसी भी भुजा की लंबाई का 1.5 गुणा भुजा से केंद्रक की लम्बवत दूरी का होता है।[14] एक त्रिभुज का केन्द्रक इसके लंबकेन्द्र H और इसके परिकेन्द्र O के बीच इसकी यूलर रेखा पर स्थित होता है, जो पूर्व की तुलना में बाद वाले के बिल्कुल दुगुने निकट होता है:[15][16]
केन्द्रक से गुजरने वाली तीन माध्यिकाओं में से कोई भी त्रिभुज के क्षेत्रफल को आधे में विभाजित करती है। यह केन्द्रक के माध्यम से अन्य रेखाओं के लिए सत्य नहीं है; समान-क्षेत्र विभाजन से सबसे बड़ा प्रसमष्टि तब होता है जब केन्द्रक के माध्यम से एक रेखा त्रिकोण के किनारे के समानांतर होती है, जिससे एक छोटा त्रिकोण और एक समलम्ब बनता है; इस सम्बन्ध में समलम्ब का क्षेत्रफल मूल त्रिभुज का 5/9 है।[17] मान लीजिए कि P त्रिभुज के समतल में कोई बिंदु है, जिसके शीर्ष A, B, और C और केन्द्रक G हैं। फिर तीन शीर्षों से P की वर्ग दूरियों का योग शीर्षों से केंद्रक G की वर्ग दूरी के योग से अधिक है। P और G के बीच की दूरी के वर्ग के तीन गुना से:[18]
एक बहुभुज का
एक गैर-स्व-प्रतिच्छेदित बंद बहुभुज का केन्द्रक n शीर्षों द्वारा परिभाषित ((x0,y0)), (x1,y1), ..., (xn−1,yn−1) बिंदु है (Cx, Cy),[21] जहाँ
एक शंकु या पिरामिड का
शंकु (ज्यामिति) या पिरामिड (ज्यामिति) का केन्द्रक रेखा खंड पर स्थित होता है जो शीर्ष (ज्यामिति) को आधार के केन्द्रक से जोड़ता है। एक ठोस शंकु या पिरामिड के लिए, केन्द्रक आधार से शीर्ष तक की दूरी का 1/4 है। एक शंकु या पिरामिड के लिए जो बिना किसी आधार के सिर्फ एक खोल है, केन्द्रक आधार तल से शीर्ष तक की दूरी का 1/3 है।
चतुष्फलक और n-आयामी सरल का एक चतुर्पाश्वीय त्रि-आयामी समष्टि में एक वस्तु है जिसके चेहरे (ज्यामिति) के रूप में चार त्रिकोण होते हैं। चतुष्फलक के शीर्ष को विपरीत फलक के केन्द्रक से मिलाने वाले रेखाखंड को माध्यिका कहते हैं और दो विपरीत किनारों के मध्यबिंदुओं को मिलाने वाले रेखाखंड को द्विमाध्यिका कहते हैं। अतः चार माध्यिकाएँ और तीन द्विमाध्यिकाएँ हैं। ये सात रेखाखंड चतुष्फलक के केन्द्रक पर मिलते हैं।[22] माध्यिकाओं को केन्द्रक द्वारा 3:1 के अनुपात में विभाजित किया जाता है। एक चतुष्फलक का केन्द्रक इसके मोंज बिंदु और परिकेंद्र (परिवृत्त क्षेत्र का केंद्र) के बीच का मध्य बिंदु है। ये तीन बिंदु चतुष्फलक की यूलर रेखा को परिभाषित करते हैं जो त्रिभुज की यूलर रेखा के समान है।
ये परिणाम निम्नलिखित तरीके से किसी भी एन-डायमेंशनल सिंप्लेक्स के लिए सामान्यीकृत होते हैं। यदि एक सिम्प्लेक्स के ऊर्ध्वाधर का समुच्य है , तो शीर्षों को सदिश (ज्यामिति) मानते हुए, केन्द्रक है
गोलार्द्ध
ठोस गोलार्द्ध का केन्द्रक (अर्थात एक ठोस गेंद का आधा) गोले के केंद्र को गोलार्द्ध के ध्रुव से 3:5 के अनुपात में जोड़ने वाले रेखा खंड को विभाजित करता है (अर्थात यह केंद्र से ध्रुव तक के रास्ते का 3/8 भाग है)।एक खोखले गोलार्ध का केन्द्रक (अर्थात एक खोखले गोले का आधा भाग) गोले के केंद्र को गोलार्ध के ध्रुव से जोड़ने वाले रेखा खंड को आधे हिस्से में विभाजित करता है।
यह भी देखें
- चेबिशेव केंद्र
- वृत्ताकार माध्य
- फ्रेचेट अर्थ
- के-अर्थ एल्गोरिथम | के-अर्थ एल्गोरिथम
- सेंट्रोइड्स की सूची
- द्रव्यमान के केंद्र का पता लगाना
- मेडॉयड
- पप्पस का केन्द्रक प्रमेय
- वर्णक्रमीय केन्द्रक
- त्रिकोण केंद्र
टिप्पणियाँ
- ↑ 1.0 1.1 Protter & Morrey (1970, p. 520)
- ↑ Protter & Morrey (1970, p. 521)
- ↑ Court, Nathan Altshiller (1960). "केन्द्रक पर नोट्स". The Mathematics Teacher. 53 (1): 33–35. doi:10.5951/MT.53.1.0033. JSTOR 27956057.
- ↑ Knorr, W. (1978). "ठोस पदार्थों के गुरुत्वाकर्षण के केंद्रों पर आर्किमिडीज का खोया हुआ ग्रंथ". The Mathematical Intelligencer (in English). 1 (2): 102–109. doi:10.1007/BF03023072. ISSN 0343-6993.
- ↑ 5.0 5.1 Altshiller-Court (1925, p. 66)
- ↑ 6.0 6.1 Protter & Morrey (1970, p. 526)
- ↑ Protter & Morrey (1970, p. 527)
- ↑ Protter & Morrey (1970, p. 528)
- ↑ Larson (1998, pp. 458–460)
- ↑ Sangwin
- ↑ Altshiller-Court (1925, p. 65)
- ↑ Kay (1969, p. 184)
- ↑ Clark Kimberling's Encyclopedia of Triangles "Encyclopedia of Triangle Centers". Archived from the original on 2012-04-19. Retrieved 2012-06-02.
- ↑ Johnson (2007, p. 173)
- ↑ Altshiller-Court (1925, p. 101)
- ↑ Kay (1969, pp. 18, 189, 225–226)
- ↑ Bottomley, Henry. "त्रिभुज की माध्यिकाएँ और क्षेत्रफल द्विभाजक". Retrieved 27 September 2013.
- ↑ 18.0 18.1 Altshiller-Court (1925, pp. 70–71)
- ↑ Kimberling, Clark (201). "सममध्य बिंदु, केन्द्रक और अन्य त्रिभुज केंद्रों के लिए त्रिरेखीय दूरी असमानताएँ". Forum Geometricorum. 10: 135–139.
- ↑ Gerald A. Edgar, Daniel H. Ullman & Douglas B. West (2018) Problems and Solutions, The American Mathematical Monthly, 125:1, 81-89, DOI: 10.1080/00029890.2018.1397465
- ↑ 21.0 21.1 Bourke (1997)
- ↑ Leung, Kam-tim; and Suen, Suk-nam; "Vectors, matrices and geometry", Hong Kong University Press, 1994, pp. 53–54
संदर्भ
- Altshiller-Court, Nathan (1925), College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd ed.), New York: Barnes & Noble, LCCN 52013504
- Bourke, Paul (July 1997). "Calculating the area and centroid of a polygon".
- Johnson, Roger A. (2007), Advanced Euclidean Geometry, Dover
- Kay, David C. (1969), College Geometry, New York: Holt, Rinehart and Winston, LCCN 69012075
- Larson, Roland E.; Hostetler, Robert P.; Edwards, Bruce H. (1998), Calculus of a Single Variable (6th ed.), Houghton Mifflin Company
- Protter, Murray H.; Morrey, Charles B. Jr. (1970), College Calculus with Analytic Geometry (2nd ed.), Reading: Addison-Wesley, LCCN 76087042
- Sangwin, C.J., Locating the centre of mass by mechanical means (PDF), archived from the original (PDF) on November 13, 2013
बाहरी संबंध
- Weisstein, Eric W. "Geometric Centroid". MathWorld.
- Encyclopedia of Triangle Centers by Clark Kimberling. The centroid is indexed as X(2).
- Characteristic Property of Centroid at cut-the-knot
- Interactive animations showing Centroid of a triangle and Centroid construction with compass and straightedge
- Experimentally finding the medians and centroid of a triangle at Dynamic Geometry Sketches, an interactive dynamic geometry sketch using the gravity simulator of Cinderella.