हंटिंग दोलन: Difference between revisions
No edit summary |
m (23 revisions imported from alpha:हंटिंग_दोलन) |
||
| (18 intermediate revisions by 2 users not shown) | |||
| Line 6: | Line 6: | ||
| image2 = Hunting oscillation plan ja 150px.gif | | image2 = Hunting oscillation plan ja 150px.gif | ||
| alt2 = | | alt2 = | ||
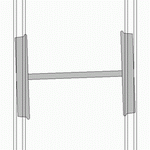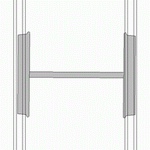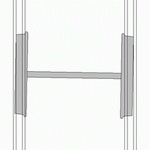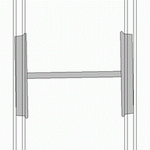
| footer = | | footer = रेलवे पहियों पर हंटिंग का दोलन | ||
}} | }} | ||
हंटिंग दोलन [[यांत्रिक संतुलन]] के बारे में [[स्व-दोलन]] है, जो सामान्यतः अवांछित है।<ref name = "OED">{{cite book | '''हंटिंग दोलन''' [[यांत्रिक संतुलन]] के बारे में [[स्व-दोलन]] है, जो सामान्यतः अवांछित है।<ref name = "OED">{{cite book | ||
| title = Oxford English Dictionary | | title = Oxford English Dictionary | ||
| url = https://archive.org/details/oxfordenglishdic0015unse | | url = https://archive.org/details/oxfordenglishdic0015unse | ||
| Line 18: | Line 18: | ||
| quote = f. The action of a machine, instrument, system, etc., that is hunting (see hunt v. 7b); an undesirable oscillation about an equilibrium speed, position, or state.}}</ref> यह अभिव्यक्ति 19वीं शताब्दी में प्रयोग में आई और यह बताती है कि प्रणाली कैसे संतुलन की खोज करती है।<ref name = "OED"/> इस अभिव्यक्ति का उपयोग इलेक्ट्रॉनिक्स, विमानन, जीव विज्ञान और रेलवे इंजीनियरिंग जैसे विविध क्षेत्रों में घटनाओं का वर्णन करने के लिए किया जाता है।<ref name = "OED"/> | | quote = f. The action of a machine, instrument, system, etc., that is hunting (see hunt v. 7b); an undesirable oscillation about an equilibrium speed, position, or state.}}</ref> यह अभिव्यक्ति 19वीं शताब्दी में प्रयोग में आई और यह बताती है कि प्रणाली कैसे संतुलन की खोज करती है।<ref name = "OED"/> इस अभिव्यक्ति का उपयोग इलेक्ट्रॉनिक्स, विमानन, जीव विज्ञान और रेलवे इंजीनियरिंग जैसे विविध क्षेत्रों में घटनाओं का वर्णन करने के लिए किया जाता है।<ref name = "OED"/> | ||
==रेलवे व्हीलसेट== | ==रेलवे व्हीलसेट== | ||
{{Main| | {{Main|व्हीलसेट (रेल परिवहन)}} | ||
मौलिक हंटिंग दोलन रेलवे वाहन की तरंगमय गति है (जिसे अधिकांशतः ट्रक हंटिंग या बोगी हंटिंग कहा जाता है) जो शंकु क्रिया के कारण होता है जिस पर [[आसंजन रेलवे|आसंजन]] [[रेलवे]] की [[दिशात्मक स्थिरता]] निर्भर करती है। यह आसंजन बलों और जड़त्व बलों की परस्पर क्रिया से उत्पन्न होता है। इस प्रकार कम गति पर, आसंजन प्रभावी हो जाता है, किंतु जैसे-जैसे गति बढ़ती है, आसंजन बल और जड़त्व बल परिमाण में तुलनीय हो जाते हैं और दोलन महत्वपूर्ण गति से प्रारंभ होता है। इस गति से ऊपर, गति हिंसक हो सकती है, जो ट्रैक और पहियों को हानि पहुंचा सकती है और संभावित रूप से [[पटरी से उतर]]ने का कारण बन सकती है। समस्या [[ विभेदक (यांत्रिक उपकरण) |विभेदक (यांत्रिक उपकरण)]] वाले प्रणाली पर उत्पन्न नहीं होती है क्योंकि क्रिया [[व्हीलसेट (रेल परिवहन)]] के दोनों पहियों पर एक ही कोणीय दर पर घूमने पर निर्भर करती है, चूँकि भिन्नताएँ दुर्लभ होते हैं, और पारंपरिक ट्रेनों के पहिए जोड़े में एक्सल से जुड़े होते हैं। [[टैल्गो 350]] की तरह, इन ट्रेनों में कोई अंतर नहीं है, फिर भी वे अधिकतर हंटिंग दोलन से प्रभावित नहीं होते हैं, क्योंकि उनके अधिकांश पहिये एक दूसरे से स्वतंत्र रूप से घूमते हैं। चूँकि, पावर कार के पहिए हंटिंग दोलन से प्रभावित हो सकते हैं, क्योंकि पावर कार के पहिए पारंपरिक बोगियों की तरह जोड़े में एक्सल से जुड़े होते हैं। कम शंक्वाकार पहिए और स्वतंत्र पहियों से सुसज्जित बोगियां जो एक-दूसरे से स्वतंत्र रूप से घूमती हैं और जोड़े में धुरी पर स्थिर नहीं होती हैं, ट्रेन की बोगियों के लिए उपयुक्त अंतर से सस्ती होती हैं।<ref>https://www.talgo.com/en/rolling-stock/very-high-speed/350/</ref> | |||
यह समस्या पहली बार 19वीं सदी के अंत में देखी गई, जब ट्रेन की गति इतनी | |||
यह समस्या पहली बार 19वीं सदी के अंत में देखी गई थी, जब ट्रेन की गति इतनी तीव्र हो गई कि इसका सामना किया जा सकता है। 1930 के दशक में इसका प्रतिकार करने के लिए गंभीर प्रयास प्रारंभ हुए, जिससे लम्बे ट्रकों और साइड-डैम्पिंग ब्लॉमबर्ग ट्रक का उदय हुआ था। जापानी [[शिंकनसेन]] के विकास में, ट्रक डिज़ाइन की गति को {{convert|225|km/h|mph|0|abbr=on}} से ऊपर बढ़ाने के लिए कम-शंक्वाकार पहियों और अन्य डिज़ाइन परिवर्तनों का उपयोग किया गया था। यूरोप और जापान में अनुसंधान और विकास प्रयासों के आधार पर पहिया और ट्रक डिजाइन में प्रगति ने स्टील व्हील प्रणाली की गति को मूल शिंकानसेन द्वारा प्राप्त गति से कहीं अधिक बढ़ा दिया है, जबकि पिछड़ी संगतता का लाभ ऐसी तकनीक को [[होवरट्रेन]] और [[मैग्लेव]] प्रणाली जैसे विकल्पों पर प्रभावी रखता है। स्टील-पहिए वाली ट्रेनों का स्पीड रिकॉर्ड फ्रांसीसी [[टीजीवी]] के निकट {{convert|574.9|km/h|mph|0|abbr=on}} है। | |||
===गतिज विश्लेषण=== | ===गतिज विश्लेषण=== | ||
[[Image:Newkinematics.png|thumb|upright=1.4|alt=Diagram, from the front, of a laterally displaced wheelset on rails (मंडलियों के रूप में प्रतिरूपित)। लेबल: पहिये की परिधि की एक रेखा पर, सीधे चलने के लिए संपर्क बिंदु की स्थिति; उस परिधि की त्रिज्या पर, नाममात्र त्रिज्या ; उस परिधि और रेल के शीर्ष के बीच की दूरी पर, पार्श्व विस्थापन; कुल मिलाकर: वक्रता केंद्र संपर्क रेखा और व्हीलसेट केंद्र रेखा का प्रतिच्छेदन है। | रेलवे व्हील कोनिंग क्रिया की गतिकी]]जबकि गुणात्मक विवरण घटना की कुछ समझ प्रदान करता है, गहरी समझ के लिए अनिवार्य रूप से वाहन [[गतिशीलता (यांत्रिकी)]] के गणितीय विश्लेषण की आवश्यकता होती है। फिर भी, परिणाम केवल अनुमानित ही हो सकते हैं। | [[Image:Newkinematics.png|thumb|upright=1.4|alt=Diagram, from the front, of a laterally displaced wheelset on rails (मंडलियों के रूप में प्रतिरूपित)। लेबल: पहिये की परिधि की एक रेखा पर, सीधे चलने के लिए संपर्क बिंदु की स्थिति; उस परिधि की त्रिज्या पर, नाममात्र त्रिज्या ; उस परिधि और रेल के शीर्ष के बीच की दूरी पर, पार्श्व विस्थापन; कुल मिलाकर: वक्रता केंद्र संपर्क रेखा और व्हीलसेट केंद्र रेखा का प्रतिच्छेदन है। | रेलवे व्हील कोनिंग क्रिया की गतिकी]]जबकि गुणात्मक विवरण घटना की कुछ समझ प्रदान करता है, गहरी समझ के लिए अनिवार्य रूप से वाहन [[गतिशीलता (यांत्रिकी)]] के गणितीय विश्लेषण की आवश्यकता होती है। फिर भी, परिणाम केवल अनुमानित ही हो सकते हैं। | ||
एक गतिज विवरण गति की [[ज्यामिति]] से संबंधित है, इसे उत्पन्न करने | एक गतिज विवरण गति की [[ज्यामिति]] से संबंधित है, इसे उत्पन्न करने वाले [[ताकत|बल]] के संदर्भ के बिना, इसलिए विश्लेषण सीधे ट्रैक पर चलने वाले व्हील सेट की ज्यामिति के विवरण के साथ प्रारंभ होता है। चूंकि न्यूटन का दूसरा नियम बलों को पिंडों के [[त्वरण]] से संबंधित करता है, इसलिए घटकों के त्वरण की गणना करके कार्य करने वाली बलों को गतिकी से प्राप्त किया जा सकता है। चूँकि, यदि ये बल गतिक विवरण को बदलते हैं (जैसा कि वे इस स्थितियों में करते हैं) तो परिणाम लगभग सही हो सकते हैं। | ||
====धारणाएं और गैर-गणितीय विवरण==== | ====धारणाएं और गैर-गणितीय विवरण==== | ||
यह गतिज वर्णन | यह गतिज वर्णन विभिन्न सरलीकृत धारणाएँ बनाता है क्योंकि यह बलों की उपेक्षा करता है। एक के लिए, यह माना जाता है कि [[रोलिंग प्रतिरोध]] शून्य है। व्हीलसेट ([[ रेलगाड़ी | रेलगाड़ी]] या [[बोगी]] से जुड़ा नहीं) को सीधे और समतल ट्रैक पर आगे की ओर धक्का दिया जाता है। व्हीलसेट किनारे पर चलना प्रारंभ कर देता है और कभी भी धीमा नहीं होता है क्योंकि इसमें कोई बल नहीं होता है (व्हीलसेट पर नीचे की ओर बल को छोड़कर जिससे यह ट्रैक पर चिपक जाए और फिसले नहीं)। यदि प्रारंभ में व्हीलसेट रेल ट्रैक पर केंद्रित है तो प्रत्येक व्हील का प्रभावी व्यास समान होता है और व्हीलसेट सदैव के लिए सम्पूर्ण रूप में सीधी रेखा में ट्रैक पर लुढ़कता है। किंतु यदि व्हीलसेट थोड़ा-सा ऑफ-सेंटर है जिससे प्रभावी व्यास (या त्रिज्या) भिन्न-भिन्न हों, तो व्हीलसेट त्रिज्या {{var|R}} के वक्र में चलना प्रारंभ कर देता है (इन पहियों की त्रिज्या आदि के आधार पर; पश्चात में प्राप्त किया जाएगा)। समस्या व्हीलसेट के प्रक्षेप पथ को खोजने के लिए गतिज तर्क का उपयोग करने की है, या अधिक स्पष्ट रूप से, ट्रैक के केंद्र में सड़क पर लंबवत रूप से प्रक्षेपित व्हीलसेट के केंद्र के प्रक्षेप पथ को खोजने के लिए हैं। यह पृथ्वी की सतह के समतल पर [[प्रक्षेपवक्र]] है और इसे {{var|x}}-{{var|y}} ग्राफिकल प्लॉट पर आलेखित किया गया है जहां {{var|x}} रेलमार्ग के साथ की दूरी है और {{var|y}} ट्रैकिंग त्रुटि है, ट्रैक के केंद्र से नीचे (दो रेलों के मध्य में) चलने वाली रेलवे की सीधी रेखा से व्हीलसेट के केंद्र का विचलन है। | ||
यह दर्शाने के लिए कि व्हीलसेट प्रक्षेपवक्र घुमावदार पथ का अनुसरण करता है, कोई व्यक्ति | यह दर्शाने के लिए कि व्हीलसेट प्रक्षेपवक्र घुमावदार पथ का अनुसरण करता है, कोई व्यक्ति समतल टेबल टॉप पर कील या पेंच रख सकता है और उसे धक्का दे सकता है। यह वृत्ताकार वक्र में घूमेगा क्योंकि कील या पेंच अत्यधिक भिन्न-भिन्न व्यास वाले पहियों वाले व्हीलसेट की तरह है। हेड बड़े व्यास के पहिये के समान है और नुकीला सिरा छोटे व्यास के पहिये के समान है। जबकि कील या पेंच पूर्ण चक्र (और अधिक) में घूमेगा, रेलरोड व्हीलसेट भिन्न तरह से व्यवहार करता है क्योंकि जैसे ही यह वक्र में मुड़ना प्रारंभ करता है, प्रभावी व्यास इस तरह से परिवर्तित होजाते हैं कि पथ की वक्रता कम हो जाती है। ध्यान दें कि त्रिज्या और वक्रता व्हीलसेट के प्रक्षेप पथ की वक्रता को संदर्भित करती है, न कि रेलवे की वक्रता को क्योंकि यह सम्पूर्ण रूप में सीधा ट्रैक है। जैसे-जैसे पहिया आगे बढ़ता है, वक्रता कम हो जाती है जब तक कि पहिये उस बिंदु तक नहीं पहुंच जाते जहां उनके प्रभावी व्यास समान होते हैं और पथ अब घुमावदार नहीं होता है। किंतु प्रक्षेपवक्र में इस बिंदु पर स्लोप है (यह सीधी रेखा है जो ट्रैक की केंद्र रेखा को तिरछे पार करती है) जिससे यह ट्रैक की केंद्र रेखा से आगे निकल जाए और प्रभावी व्यास उलट जाता है (पहले छोटा व्यास वाला पहिया बड़ा व्यास और इसके विपरीत बन जाता है)। इसका परिणाम यह होता है कि पहिया विपरीत दिशा में वक्र में घूमने लगता है। यह फिर से केंद्र रेखा से आगे निकल जाता है और यह घटना पहिये के निकट से दोलन के साथ अनिश्चित काल तक जारी रहती है। ध्यान दें कि व्हील [[ निकला हुआ |फ्लैंज]] कभी भी रेल से संपर्क नहीं बनाता है। इस मॉडल में, रेल को सदैव रेल हेड पर ही लाइन के साथ व्हील ट्रेड से संपर्क करने के लिए माना जाता है, जो मानता है कि रेल चाकू की धार वाली हैं और केवल लाइन (शून्य चौड़ाई) के साथ व्हील ट्रेड के साथ संपर्क बनाती हैं। | ||
====गणितीय विश्लेषण==== | ====गणितीय विश्लेषण==== | ||
पहिए के टायर के शंक्वाकार आकार के कारण ट्रेन पटरी पर टिकी रहती है। यदि व्हीलसेट को | पहिए के टायर के शंक्वाकार आकार के कारण ट्रेन पटरी पर टिकी रहती है। यदि व्हीलसेट को {{var|y}} (ट्रैकिंग त्रुटि) द्वारा एक तरफ से कुछ मात्रा में विस्थापित किया जाता है, तो एक तरफ रेल के संपर्क में चलने की त्रिज्या कम हो जाती है, जबकि दूसरी तरफ बढ़ जाती है। [[कोणीय वेग]] दोनों पहियों के लिए समान है (वे [[कठोरता]] धुरी के माध्यम से जुड़े हुए हैं), इसलिए बड़े [[व्यास]] वाले चलने की गति तेज हो जाती है, जबकि छोटे व्यास वाले की गति धीमी हो जाती है। व्हील सेट रेल पर पहियों के साथ संपर्क के बिंदुओं और व्हील सेट की धुरी से निकलने वाले शंकु के जनरेटर के चौराहे द्वारा परिभाषित वक्रता के केंद्र के चारों ओर घूमता है। [[समरूप त्रिभुज]] को प्रयुक्त करने पर, हमें टर्न त्रिज्या प्राप्त होती है: | ||
[[Image:NewTurnRadius.png|thumb|केंद्र|सीधा=1.4|घूमने की त्रिज्या की गणना]] | [[Image:NewTurnRadius.png|thumb|केंद्र|सीधा=1.4|घूमने की त्रिज्या की गणना]] | ||
{{block indent|<math>\frac{1}{R} =\frac{2ky}{rd}</math>}} | {{block indent|<math>\frac{1}{R} =\frac{2ky}{rd}</math>}} | ||
जहाँ {{var|d}} ट्रैक [[रेल गेज]] है, सीधे चलने पर पहिए की त्रिज्या {{var|r}} और {{var|k}} ट्रेड [[मशीन टेपर]] है (जो ट्रैक के लंबवत क्षैतिज दिशा में ट्रेड का स्लोप है)। | |||
सीधे ट्रैक के सापेक्ष पहिये का पथ | सीधे ट्रैक के सापेक्ष पहिये का पथ फलन {{var|y}}({{var|x}}) द्वारा परिभाषित किया गया है, जहाँ {{var|x}} ट्रैक पर प्रगति है। इसे कभी-कभी ट्रैकिंग त्रुटि भी कहा जाता है।<ref>Tracking error will be zero if the path of the wheels runs absolutely straight along the track and the wheel pair is centered on the track.</ref> परंतु गति की दिशा कमोबेश रेल के [[समानांतर (ज्यामिति)]] बनी रहे, पथ की [[वक्रता]] लगभग ट्रैक के साथ दूरी के संबंध में {{var|y}} के दूसरे व्युत्पन्न से संबंधित हो सकती है <ref>See [[Curvature#Graph of a function]] for mathematical details. The approximate equality becomes equality only when the tracking error, {{var|y}}, has zero slope with respect to {{var|x}}. Since the tracking error will turn out to be a sine wave, the points of zero slope are at the points of maximum tracking error {{var|y}}. But the equality is approximately correct provided the slope of {{var|y}} is low.</ref> | ||
{{block indent|<math>\left|\frac{\operatorname{d}^2y}{\operatorname{d}x^2}\right| \approx \frac{1}{R}</math>}} | {{block indent|<math>\left|\frac{\operatorname{d}^2y}{\operatorname{d}x^2}\right| \approx \frac{1}{R}</math>}} | ||
| Line 47: | Line 48: | ||
यह तरंग दैर्ध्य वाली सरल हार्मोनिक गति है: | यह तरंग दैर्ध्य वाली सरल हार्मोनिक गति है: | ||
{{block indent|<math>\lambda = 2\pi \sqrt{\frac{rd}{2k}}</math>{{pad|3em}} | {{block indent|<math>\lambda = 2\pi \sqrt{\frac{rd}{2k}}</math>{{pad|3em}}क्लिंगेल सूत्र के नाम से जाना जाता है (derived in 1883)<ref>Iwnicki, p.7 formula 2.1</ref>}} | ||
इस गतिक विश्लेषण से पता चलता है कि रेलगाड़ियाँ हर समय एक ओर से दूसरी ओर घूमती रहती हैं। वास्तव में, यह दोलन महत्वपूर्ण गति से नीचे डंपिंग अनुपात है और सवारी तदनुसार अधिक आरामदायक है। गतिज परिणाम गति उत्पन्न करने वाली शक्तियों की उपेक्षा करता है। इनका विश्लेषण | इस गतिक विश्लेषण से पता चलता है कि रेलगाड़ियाँ हर समय एक ओर से दूसरी ओर घूमती रहती हैं। वास्तव में, यह दोलन महत्वपूर्ण गति से नीचे डंपिंग अनुपात है और सवारी तदनुसार अधिक आरामदायक है। गतिज परिणाम गति उत्पन्न करने वाली शक्तियों की उपेक्षा करता है। इनका विश्लेषण क्रीप (गैर-रैखिक) की अवधारणा का उपयोग करके किया जा सकता है, किंतु इन्हें सरलता से मापना कुछ सीमा तक सम्मिश्र है, क्योंकि वे संपर्क के क्षेत्रों में पहिया और रेल के [[हर्ट्ज़ियन संपर्क तनाव]] से उत्पन्न होते हैं। ये [[घर्षण संपर्क यांत्रिकी]] के विषय हैं; हंटिंग गति विश्लेषण में इन प्रभावों को सम्मिलित करने वाली प्रारंभिक प्रस्तुति कार्टर द्वारा प्रस्तुत की गई थी।<ref name=Carter1928>{{cite journal|last=Carter|first=F. W.|title=लोकोमोटिव के संचालन की स्थिरता पर|journal=Proceedings of the Royal Society|date=July 25, 1928|volume=121|issue=788|series=A|pages=585–610|doi=10.1098/rspa.1928.0220|bibcode = 1928RSPSA.121..585C |doi-access=free}}</ref> ऐतिहासिक अवलोकन के लिए नॉथे देखें।<ref name=Knothe2008>{{cite journal|last=Knothe|first=K.|title=History of wheel/rail contact mechanics: from Redtenbacher to Kalker|journal=Vehicle System Dynamics|year=2008|volume=46|issue=1–2|pages=9–26|doi=10.1080/00423110701586469|s2cid=109580328}}</ref> | ||
यदि गति | यदि गति अधिक सीमा तक रेल के समानांतर है, तो व्हील सेट <math>\left(\theta\right)</math> का कोणीय विस्थापन इस प्रकार दिया जाता है: | ||
{{block indent|<math>\theta = \frac{\operatorname{d}y}{\operatorname{d}x}</math>}} | {{block indent|<math>\theta = \frac{\operatorname{d}y}{\operatorname{d}x}</math>}} | ||
| Line 60: | Line 61: | ||
\end{align}</math>}} | \end{align}</math>}} | ||
कोणीय विक्षेपण भी सरल हार्मोनिक गति का अनुसरण करता है, जो चक्र के एक चौथाई तक | कोणीय विक्षेपण भी सरल हार्मोनिक गति का अनुसरण करता है, जो चक्र के एक चौथाई तक निकट की गति से पीछे रहता है। विभिन्न प्रणालियों में, जिनमें दो भिन्न-भिन्न अवस्थाओं (इस स्थितियों में एक्सल यॉ विक्षेपण और पार्श्व विस्थापन) से युक्त हार्मोनिक गति की विशेषता होती है, दो गतियों के मध्य का चौथाई चक्र अंतराल प्रणाली को आगे की गति से ऊर्जा निकालने की क्षमता प्रदान करता है। यह प्रभाव विमान के पंखों के कंपन और सड़क वाहनों की गति के डगमगाने के साथ-साथ रेलवे वाहनों के हंटिंग में भी देखा जाता है। ऊपर प्राप्त गतिक समाधान क्रांतिक गति पर गति का वर्णन करता है। | ||
व्यवहार में, क्रांतिक गति से नीचे, दो गतियों के | व्यवहार में, क्रांतिक गति से नीचे, दो गतियों के मध्य अंतराल एक चौथाई चक्र से कम होता है जिससे गति कम हो जाती है, किंतु, महत्वपूर्ण गति से ऊपर, अंतराल एक चौथाई चक्र से अधिक होता है जिससे गति बढ़ जाती है। | ||
जड़त्वीय बलों का अनुमान लगाने के लिए, दूरी व्युत्पन्न को समय व्युत्पन्न के रूप में व्यक्त करना आवश्यक है। यह वाहन की गति | जड़त्वीय बलों का अनुमान लगाने के लिए, दूरी व्युत्पन्न को समय व्युत्पन्न के रूप में व्यक्त करना आवश्यक है। यह वाहन की गति {{var|U}} का उपयोग करके किया जाता है, जिसे स्थिर माना जाता है: | ||
{{block indent|<math> \frac{\operatorname{d}}{\operatorname{d}t} = U\frac{\operatorname{d}}{\operatorname{d}x}</math>}} | {{block indent|<math> \frac{\operatorname{d}}{\operatorname{d}t} = U\frac{\operatorname{d}}{\operatorname{d}x}</math>}} | ||
| Line 72: | Line 73: | ||
{{block indent|<math>Fd = C \frac{\operatorname{d}^2 \theta}{\operatorname{d}t^2}</math>}} | {{block indent|<math>Fd = C \frac{\operatorname{d}^2 \theta}{\operatorname{d}t^2}</math>}} | ||
जहाँ {{var|F}} रेल के साथ कार्य करने वाला बल है और {{var|C}} व्हील सेट की जड़ता का क्षण है। | |||
{{block indent|<math>F = -C U^2 \left(\frac{2k}{rd^2}\right) \theta</math>}} | {{block indent|<math>F = -C U^2 \left(\frac{2k}{rd^2}\right) \theta</math>}} | ||
पहिये और रेल के | पहिये और रेल के मध्य अधिकतम घर्षण बल निम्न द्वारा दिया जाता है: | ||
{{block indent|<math>F = \mu \frac{W}{2}</math>}} | {{block indent|<math>F = \mu \frac{W}{2}</math>}} | ||
जहाँ {{var|W}} एक्सल लोड है और <math>\mu</math> घर्षण का गुणांक है। निम्नलिखित द्वारा दी गई गति और धुरी विक्षेपण के संयोजन पर ग्रॉस फिसलन होगी: | |||
{{block indent|<math>\theta U^2 = \mu W \frac{rd^2}{4Ck}</math>}} | {{block indent|<math>\theta U^2 = \mu W \frac{rd^2}{4Ck}</math>}} | ||
यह अभिव्यक्ति महत्वपूर्ण गति का महत्वपूर्ण अधिक अनुमान देती है, | यह अभिव्यक्ति महत्वपूर्ण गति का महत्वपूर्ण अधिक अनुमान देती है, किंतु यह उस भौतिक कारण को स्पष्ट करती है कि हंटिंग क्यों होता है, अर्थात जड़त्वीय बल निश्चित गति से ऊपर आसंजन बलों के साथ तुलनीय हो जाते हैं। इस स्थितियों में घर्षण को सीमित करना आसंजन बल का खराब प्रतिनिधित्व है। | ||
वास्तविक आसंजन बल संपर्क के क्षेत्र में ट्रेड और रेल की विकृति से उत्पन्न होते हैं। कोई स्थूल फिसलन नहीं है, केवल लोचदार विकृति और कुछ स्थानीय फिसलन ( | वास्तविक आसंजन बल संपर्क के क्षेत्र में ट्रेड और रेल की विकृति से उत्पन्न होते हैं। कोई स्थूल फिसलन नहीं है, केवल लोचदार विकृति और कुछ स्थानीय फिसलन (क्रीप फिसलन) है। सामान्य ऑपरेशन के समय ये बल सीमित घर्षण बाधा के अन्दर होते हैं। घर्षण संपर्क यांत्रिकी सिद्धांतों का उपयोग करते हुए संपूर्ण विश्लेषण इन बलों को ध्यान में रखता है। | ||
चूँकि, गतिक विश्लेषण ने माना कि व्हील-रेल संपर्क में सम्पूर्ण रूप में भी फिसलन नहीं थी। अब यह स्पष्ट है कि कुछ रेंगने वाली फिसलन है जो व्हीलसेट के परिकलित साइनसॉइडल प्रक्षेपवक्र (क्लिंगल के सूत्र के अनुसार) को सम्पूर्ण रूप में सही नहीं बनाती है। | |||
===[[ऊर्जा]] संतुलन=== | ===[[ऊर्जा]] संतुलन=== | ||
क्रांतिक गति का अनुमान प्राप्त करने के लिए, हम इस तथ्य का उपयोग करते हैं कि जिस स्थिति के लिए यह गतिज समाधान वैध है वह उस स्थिति से मेल खाती है जहां परिवेश के साथ कोई शुद्ध ऊर्जा विनिमय नहीं होता है, इसलिए [[गतिज ऊर्जा]] और [[संभावित ऊर्जा]] पर विचार करके | क्रांतिक गति का अनुमान प्राप्त करने के लिए, हम इस तथ्य का उपयोग करते हैं कि जिस स्थिति के लिए यह गतिज समाधान वैध है वह उस स्थिति से मेल खाती है जहां परिवेश के साथ कोई शुद्ध ऊर्जा विनिमय नहीं होता है, इसलिए [[गतिज ऊर्जा]] और [[संभावित ऊर्जा]] पर विचार करके प्रणाली, हमें महत्वपूर्ण गति प्राप्त करने में सक्षम होना चाहिए। | ||
माना: | |||
{{block indent|<math> \omega = \frac{\operatorname{d}\theta}{\operatorname{d}t}</math>}} | {{block indent|<math> \omega = \frac{\operatorname{d}\theta}{\operatorname{d}t}</math>}} | ||
| Line 97: | Line 98: | ||
{{block indent|<math> \omega \frac{\operatorname{d}}{\operatorname{d}\theta} = \frac{\operatorname{d}}{\operatorname{d}t}</math>}} | {{block indent|<math> \omega \frac{\operatorname{d}}{\operatorname{d}\theta} = \frac{\operatorname{d}}{\operatorname{d}t}</math>}} | ||
कोणीय त्वरण समीकरण को यव में कोणीय वेग के संदर्भ में व्यक्त किया जा सकता है, | कोणीय त्वरण समीकरण को यव में कोणीय वेग <math>\omega</math> के संदर्भ में व्यक्त किया जा सकता है, : | ||
{{block indent|<math>\omega \frac{\operatorname{d}\omega}{\operatorname{d}\theta} = -U^2 \left(\frac{2k}{rd}\right) \theta</math>}} | {{block indent|<math>\omega \frac{\operatorname{d}\omega}{\operatorname{d}\theta} = -U^2 \left(\frac{2k}{rd}\right) \theta</math>}} | ||
| Line 109: | Line 110: | ||
{{block indent|<math>\frac{d}{cos(\theta)} = d\left(1 + \frac{1}{2} \theta^2\right)</math>}} | {{block indent|<math>\frac{d}{cos(\theta)} = d\left(1 + \frac{1}{2} \theta^2\right)</math>}} | ||
(छोटी मात्रा के दूसरे क्रम तक) | (छोटी मात्रा के दूसरे क्रम तक) ट्रेडों के केंद्रों से समर्थन बिंदु का विस्थापन है: | ||
ट्रेडों के केंद्रों से समर्थन बिंदु का विस्थापन है: | |||
{{block indent|<math>\frac{1}{2} \left(d + \frac{1}{2}d \theta^2 - d\right)</math>}} | {{block indent|<math>\frac{1}{2} \left(d + \frac{1}{2}d \theta^2 - d\right)</math>}} | ||
| Line 119: | Line 119: | ||
{{block indent|<math>E = \frac{1}{4} Wkd \theta^2</math>}} | {{block indent|<math>E = \frac{1}{4} Wkd \theta^2</math>}} | ||
यह | यह प्रणाली से लुप्त ऊर्जा है, इसलिए गति जारी रखने के लिए, व्हीलसेट की आगे की गति से समान मात्रा में ऊर्जा निकाली जानी चाहिए। | ||
बाहरी पहिये का वेग निम्न द्वारा दिया गया है: | बाहरी पहिये का वेग निम्न द्वारा दिया गया है: | ||
| Line 135: | Line 135: | ||
{{block indent|<math>\delta E = \frac{1}{2} m \left(\frac{Uky}{r}\right)^2</math>}} | {{block indent|<math>\delta E = \frac{1}{2} m \left(\frac{Uky}{r}\right)^2</math>}} | ||
गति निरंतर आयाम पर तब तक जारी रहेगी जब तक आगे की गति से निकाली गई ऊर्जा, और शून्य यॉ पर सेट किए गए पहिये की बढ़ी हुई गतिज ऊर्जा के रूप में प्रकट होती है, अधिकतम यॉ पर धुरी भार को कम करने से | गति निरंतर आयाम पर तब तक जारी रहेगी जब तक आगे की गति से निकाली गई ऊर्जा, और शून्य यॉ पर सेट किए गए पहिये की बढ़ी हुई गतिज ऊर्जा के रूप में प्रकट होती है, अधिकतम यॉ पर धुरी भार को कम करने से लुप्त संभावित ऊर्जा के समान है . | ||
अब, किनेमेटिक्स से: | अब, किनेमेटिक्स से: | ||
| Line 143: | Line 143: | ||
\end{align}</math>}} | \end{align}</math>}} | ||
किंतु | |||
{{block indent|<math>\omega^2 = -U^2 \left(\frac{2k}{rd}\right) \theta^2</math>}} | {{block indent|<math>\omega^2 = -U^2 \left(\frac{2k}{rd}\right) \theta^2</math>}} | ||
| Line 158: | Line 158: | ||
{{block indent|<math>U^2 = \frac{Wrd^2}{4C + md^2}</math>}} | {{block indent|<math>U^2 = \frac{Wrd^2}{4C + md^2}</math>}} | ||
यह व्हील टेपर से स्वतंत्र है, | यह व्हील टेपर से स्वतंत्र है, किंतु एक्सल [[संरचनात्मक भार]] और व्हील सेट द्रव्यमान के अनुपात पर निर्भर करता है। यदि धागों का आकार वास्तव में शंक्वाकार होता, तो क्रांतिक गति टेपर से स्वतंत्र होती। व्यवहार में, पहिये पर घिसाव के कारण टेपर चलने की चौड़ाई में भिन्न होता है, जिससे संभावित ऊर्जा निर्धारित करने के लिए उपयोग किए जाने वाले टेपर का मूल्य गतिज ऊर्जा की गणना करने के लिए उपयोग किए जाने वाले से भिन्न होता है। पूर्व को इस रूप में निरूपित करना {{var|a}}, क्रांतिक गति बन जाती है: | ||
{{block indent|<math>U^2=\frac{Ward^2}{k(4C+md^2)} </math>}} | {{block indent|<math>U^2=\frac{Ward^2}{k(4C+md^2)} </math>}} | ||
कहाँ {{var|a}} अब पहिए की [[घिसाव]]ट से निर्धारित होने वाला आकार कारक है। यह परिणाम विकेंस (1965) में प्राप्त हुआ है<ref name=Wickens1965>{{cite journal|last=Wickens|first=A. H.|title=The Dynamics of Railway Vehicles on Straight Track: Fundamental Considerations of Lateral Stability|journal=[[Proceedings of the Institution of Mechanical Engineers]]|year=1965–66|pages=29–}}</ref> मानक [[नियंत्रण इंजीनियरिंग]] विधियों का उपयोग करके | कहाँ {{var|a}} अब पहिए की [[घिसाव]]ट से निर्धारित होने वाला आकार कारक है। यह परिणाम विकेंस (1965) में प्राप्त हुआ है <ref name=Wickens1965>{{cite journal|last=Wickens|first=A. H.|title=The Dynamics of Railway Vehicles on Straight Track: Fundamental Considerations of Lateral Stability|journal=[[Proceedings of the Institution of Mechanical Engineers]]|year=1965–66|pages=29–}}</ref> मानक [[नियंत्रण इंजीनियरिंग]] विधियों का उपयोग करके प्रणाली गतिशीलता के विश्लेषण से किया जाता है। | ||
===सरलीकृत विश्लेषण की सीमा=== | ===सरलीकृत विश्लेषण की सीमा=== | ||
इस विश्लेषण से पता चलता है कि व्हील सेट की गति कहीं अधिक | इस विश्लेषण से पता चलता है कि व्हील सेट की गति कहीं अधिक सम्मिश्र है। वाहन के निलंबन द्वारा अतिरिक्त निरोधक बल लगाए जाते हैं <ref>{{cite journal|last=Wickens|first=A. H. |last2=Gilchrist |first2=A. O. |first3=A. E. W. |last3=Hobbs |title=उच्च प्रदर्शन वाले दो-एक्सल मालवाहक वाहनों के लिए सस्पेंशन डिज़ाइन|journal=Proceedings of the Institution of Mechanical Engineers|year=1969–70|pages=22–}}</ref> और, उच्च गति पर, व्हील सेट अतिरिक्त [[जाइरोस्कोपिक]] टॉर्क उत्पन्न करेगा, जो महत्वपूर्ण गति के अनुमान को संशोधित करेगा। परंपरागत रूप से रेलवे वाहन कम गति में स्थिर गति रखता है, जब यह उच्च गति तक पहुंचता है तो स्थिरता अस्थिर रूप में परिवर्तित होजाती है। रेल वाहन प्रणाली की गतिशीलता के गैर-रेखीय विश्लेषण का मुख्य उद्देश्य स्पर्शरेखा ट्रैक में रेल वाहनों के द्विभाजन, गैर-रेखीय पार्श्व स्थिरता और हंटिंग व्यवहार की विश्लेषणात्मक जांच का दृश्य दिखाना है। यह अध्ययन विश्लेषण के लिए बोगोलीउबोव विधि का वर्णन करता है।<ref>{{cite journal|last=Serajian|first=Reza |title=एक बोगी के शिकार व्यवहार के गैर-रेखीय विश्लेषण पर विभिन्न पार्श्व कठोरता के साथ पैरामीटर्स का बदलता प्रभाव|journal=Journal of Measurements in Engineering|year=2013|pages=195–206}}</ref> दो मुख्य स्थिति, अर्थात् निकाय को निश्चित समर्थन के रूप में मानना और हंटिंग की गति की गणना में गैर-रेखीय तत्वों का प्रभाव, अधिकतर अध्ययनों में केंद्रित हैं।<ref>{{cite journal|last=Serajian|first=Reza |title=हॉपफ द्विभाजन सिद्धांत द्वारा मान्यता प्राप्त नॉनलाइनियर व्हील-सेट शिकार पर बोगी और शरीर की जड़ता का प्रभाव|journal=Int J Auto Engng|year=2011|pages=186–196}}</ref> वास्तविक रेलवे वाहन में स्वतंत्रता की विभिन्न और डिग्री होती हैं और परिणामस्वरूप, एक से अधिक महत्वपूर्ण गति हो सकती है; यह किसी भी तरह से निश्चित नहीं है कि निम्नतम पहिए की गति से स्थिर होता है। चूँकि, विश्लेषण शिक्षाप्रद है क्योंकि यह दिखाता है कि हंटिंग क्यों होता है। जैसे-जैसे गति बढ़ती है, जड़त्वीय बल आसंजन बलों के साथ तुलनीय हो जाते हैं। इसीलिए महत्वपूर्ण गति धुरी भार (जो आसंजन बल निर्धारित करती है) और व्हीलसेट द्रव्यमान (जो जड़त्व बल निर्धारित करती है) के अनुपात पर निर्भर करती है। | ||
दो मुख्य | |||
वैकल्पिक रूप से, निश्चित गति से नीचे, आगे की गति से जो ऊर्जा निकाली जाती है, वह धुरियों को नीचे करने से | वैकल्पिक रूप से, निश्चित गति से नीचे, आगे की गति से जो ऊर्जा निकाली जाती है, वह धुरियों को नीचे करने से लुप्त ऊर्जा को बदलने के लिए अपर्याप्त होती है और गति नम हो जाती है; इस गति से ऊपर, निकाली गई ऊर्जा संभावित ऊर्जा में हानि से अधिक होती है और आयाम बनता है। | ||
अधिकतम एक्सल यॉ पर संभावित ऊर्जा को एक्सल की यॉ गति पर लोचदार बाधा को | अधिकतम एक्सल यॉ पर संभावित ऊर्जा को एक्सल की यॉ गति पर लोचदार बाधा को सम्मिलित करके बढ़ाया जा सकता है, जिससे स्प्रिंग तनाव से उत्पन्न होने वाला योगदान हो। पहियों की यॉ गति पर बाधा को बढ़ाने के लिए बोगियों में पहियों की व्यवस्था करना और बोगी में लोचदार बाधाओं को प्रयुक्त करने से भी महत्वपूर्ण गति बढ़ जाती है। समीकरण में लोचदार बलों का परिचय निलंबन डिजाइनों की अनुमति देता है जो मौलिक हंटिंग के अतिरिक्त केवल सकल फिसलन की प्रारंभ तक सीमित होते हैं। हंटिंग के आभासी उन्मूलन के लिए भुगतान किया जाने वाला जुर्माना सीधा रास्ता है, जिसमें रास्ते के अधिकार की समस्या और विरासत के सम्मिश्र प्रारूप के साथ असंगतता सम्मिलित है। | ||
हंटिंग गतिशील समस्या है जिसे कम से कम सैद्धांतिक रूप से सक्रिय फीडबैक नियंत्रण द्वारा हल किया जा सकता है, जिसे ट्रैक की गुणवत्ता के अनुसार अनुकूलित किया जा सकता है। | हंटिंग गतिशील समस्या है जिसे कम से कम सैद्धांतिक रूप से सक्रिय फीडबैक नियंत्रण द्वारा हल किया जा सकता है, जिसे ट्रैक की गुणवत्ता के अनुसार अनुकूलित किया जा सकता है। चूँकि, सक्रिय नियंत्रण की प्रारंभ विश्वसनीयता और सुरक्षा के उद्देश्यों को उठाती है। | ||
हंटिंग | हंटिंग प्रारंभ होने के कुछ ही समय पश्चात, भारी फिसलन होती है और पहिए के फ्लैंज पटरियों पर प्रभाव डालते हैं, जिससे संभावित रूप से दोनों को हानि होता है। | ||
===सड़क-रेल वाहन=== | ===सड़क-रेल वाहन=== | ||
[[File:Road-rail vehicle conversion to Toyota Land Cruiser.jpg|thumb|स्वतंत्र रेल व्हील एक्सल सड़क-रेल वाहनों पर | [[File:Road-rail vehicle conversion to Toyota Land Cruiser.jpg|thumb|स्वतंत्र रेल व्हील एक्सल सड़क-रेल वाहनों पर सामान्य हैं]]विभिन्न सड़क-रेल वाहनों में प्रत्येक रेल पहिये पर स्वतंत्र धुरी और निलंबन प्रणाली होती है। जब इसे रेल पर सड़क पहियों की उपस्थिति के साथ जोड़ा जाता है तो उपरोक्त सूत्रों का उपयोग करना सम्मिश्र हो जाता है। ऐतिहासिक रूप से, सड़क-रेल वाहनों के अगले पहिये थोड़े-से अंदर की ओर सेट होते हैं, जिससे वाहन को रेल पर चलाते समय हंटिंग को कम करने में सहायता मिलती है। | ||
== यह भी देखें == | == यह भी देखें == | ||
| Line 183: | Line 182: | ||
* [[रेल आसंजन]] | * [[रेल आसंजन]] | ||
* [[रेल प्रोफ़ाइल]] | * [[रेल प्रोफ़ाइल]] | ||
* गति का | * गति का वोबल | ||
* [[वाहन की गतिशीलता]] | * [[वाहन की गतिशीलता]] | ||
* व्हीलसेट (रेल परिवहन) | * व्हीलसेट (रेल परिवहन) | ||
इस वर्ग की समस्या से | इस वर्ग की समस्या से सामना करने के सामान्य विधियों के लिए देखें | ||
* नियंत्रण इंजीनियरिंग | * नियंत्रण इंजीनियरिंग | ||
| Line 206: | Line 205: | ||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On 11/08/2023]] | [[Category:Created On 11/08/2023]] | ||
[[Category:Vigyan Ready]] | |||
Latest revision as of 07:09, 27 September 2023
हंटिंग दोलन यांत्रिक संतुलन के बारे में स्व-दोलन है, जो सामान्यतः अवांछित है।[1] यह अभिव्यक्ति 19वीं शताब्दी में प्रयोग में आई और यह बताती है कि प्रणाली कैसे संतुलन की खोज करती है।[1] इस अभिव्यक्ति का उपयोग इलेक्ट्रॉनिक्स, विमानन, जीव विज्ञान और रेलवे इंजीनियरिंग जैसे विविध क्षेत्रों में घटनाओं का वर्णन करने के लिए किया जाता है।[1]
रेलवे व्हीलसेट
मौलिक हंटिंग दोलन रेलवे वाहन की तरंगमय गति है (जिसे अधिकांशतः ट्रक हंटिंग या बोगी हंटिंग कहा जाता है) जो शंकु क्रिया के कारण होता है जिस पर आसंजन रेलवे की दिशात्मक स्थिरता निर्भर करती है। यह आसंजन बलों और जड़त्व बलों की परस्पर क्रिया से उत्पन्न होता है। इस प्रकार कम गति पर, आसंजन प्रभावी हो जाता है, किंतु जैसे-जैसे गति बढ़ती है, आसंजन बल और जड़त्व बल परिमाण में तुलनीय हो जाते हैं और दोलन महत्वपूर्ण गति से प्रारंभ होता है। इस गति से ऊपर, गति हिंसक हो सकती है, जो ट्रैक और पहियों को हानि पहुंचा सकती है और संभावित रूप से पटरी से उतरने का कारण बन सकती है। समस्या विभेदक (यांत्रिक उपकरण) वाले प्रणाली पर उत्पन्न नहीं होती है क्योंकि क्रिया व्हीलसेट (रेल परिवहन) के दोनों पहियों पर एक ही कोणीय दर पर घूमने पर निर्भर करती है, चूँकि भिन्नताएँ दुर्लभ होते हैं, और पारंपरिक ट्रेनों के पहिए जोड़े में एक्सल से जुड़े होते हैं। टैल्गो 350 की तरह, इन ट्रेनों में कोई अंतर नहीं है, फिर भी वे अधिकतर हंटिंग दोलन से प्रभावित नहीं होते हैं, क्योंकि उनके अधिकांश पहिये एक दूसरे से स्वतंत्र रूप से घूमते हैं। चूँकि, पावर कार के पहिए हंटिंग दोलन से प्रभावित हो सकते हैं, क्योंकि पावर कार के पहिए पारंपरिक बोगियों की तरह जोड़े में एक्सल से जुड़े होते हैं। कम शंक्वाकार पहिए और स्वतंत्र पहियों से सुसज्जित बोगियां जो एक-दूसरे से स्वतंत्र रूप से घूमती हैं और जोड़े में धुरी पर स्थिर नहीं होती हैं, ट्रेन की बोगियों के लिए उपयुक्त अंतर से सस्ती होती हैं।[2]
यह समस्या पहली बार 19वीं सदी के अंत में देखी गई थी, जब ट्रेन की गति इतनी तीव्र हो गई कि इसका सामना किया जा सकता है। 1930 के दशक में इसका प्रतिकार करने के लिए गंभीर प्रयास प्रारंभ हुए, जिससे लम्बे ट्रकों और साइड-डैम्पिंग ब्लॉमबर्ग ट्रक का उदय हुआ था। जापानी शिंकनसेन के विकास में, ट्रक डिज़ाइन की गति को 225 km/h (140 mph) से ऊपर बढ़ाने के लिए कम-शंक्वाकार पहियों और अन्य डिज़ाइन परिवर्तनों का उपयोग किया गया था। यूरोप और जापान में अनुसंधान और विकास प्रयासों के आधार पर पहिया और ट्रक डिजाइन में प्रगति ने स्टील व्हील प्रणाली की गति को मूल शिंकानसेन द्वारा प्राप्त गति से कहीं अधिक बढ़ा दिया है, जबकि पिछड़ी संगतता का लाभ ऐसी तकनीक को होवरट्रेन और मैग्लेव प्रणाली जैसे विकल्पों पर प्रभावी रखता है। स्टील-पहिए वाली ट्रेनों का स्पीड रिकॉर्ड फ्रांसीसी टीजीवी के निकट 574.9 km/h (357 mph) है।
गतिज विश्लेषण
जबकि गुणात्मक विवरण घटना की कुछ समझ प्रदान करता है, गहरी समझ के लिए अनिवार्य रूप से वाहन गतिशीलता (यांत्रिकी) के गणितीय विश्लेषण की आवश्यकता होती है। फिर भी, परिणाम केवल अनुमानित ही हो सकते हैं।
एक गतिज विवरण गति की ज्यामिति से संबंधित है, इसे उत्पन्न करने वाले बल के संदर्भ के बिना, इसलिए विश्लेषण सीधे ट्रैक पर चलने वाले व्हील सेट की ज्यामिति के विवरण के साथ प्रारंभ होता है। चूंकि न्यूटन का दूसरा नियम बलों को पिंडों के त्वरण से संबंधित करता है, इसलिए घटकों के त्वरण की गणना करके कार्य करने वाली बलों को गतिकी से प्राप्त किया जा सकता है। चूँकि, यदि ये बल गतिक विवरण को बदलते हैं (जैसा कि वे इस स्थितियों में करते हैं) तो परिणाम लगभग सही हो सकते हैं।
धारणाएं और गैर-गणितीय विवरण
यह गतिज वर्णन विभिन्न सरलीकृत धारणाएँ बनाता है क्योंकि यह बलों की उपेक्षा करता है। एक के लिए, यह माना जाता है कि रोलिंग प्रतिरोध शून्य है। व्हीलसेट ( रेलगाड़ी या बोगी से जुड़ा नहीं) को सीधे और समतल ट्रैक पर आगे की ओर धक्का दिया जाता है। व्हीलसेट किनारे पर चलना प्रारंभ कर देता है और कभी भी धीमा नहीं होता है क्योंकि इसमें कोई बल नहीं होता है (व्हीलसेट पर नीचे की ओर बल को छोड़कर जिससे यह ट्रैक पर चिपक जाए और फिसले नहीं)। यदि प्रारंभ में व्हीलसेट रेल ट्रैक पर केंद्रित है तो प्रत्येक व्हील का प्रभावी व्यास समान होता है और व्हीलसेट सदैव के लिए सम्पूर्ण रूप में सीधी रेखा में ट्रैक पर लुढ़कता है। किंतु यदि व्हीलसेट थोड़ा-सा ऑफ-सेंटर है जिससे प्रभावी व्यास (या त्रिज्या) भिन्न-भिन्न हों, तो व्हीलसेट त्रिज्या R के वक्र में चलना प्रारंभ कर देता है (इन पहियों की त्रिज्या आदि के आधार पर; पश्चात में प्राप्त किया जाएगा)। समस्या व्हीलसेट के प्रक्षेप पथ को खोजने के लिए गतिज तर्क का उपयोग करने की है, या अधिक स्पष्ट रूप से, ट्रैक के केंद्र में सड़क पर लंबवत रूप से प्रक्षेपित व्हीलसेट के केंद्र के प्रक्षेप पथ को खोजने के लिए हैं। यह पृथ्वी की सतह के समतल पर प्रक्षेपवक्र है और इसे x-y ग्राफिकल प्लॉट पर आलेखित किया गया है जहां x रेलमार्ग के साथ की दूरी है और y ट्रैकिंग त्रुटि है, ट्रैक के केंद्र से नीचे (दो रेलों के मध्य में) चलने वाली रेलवे की सीधी रेखा से व्हीलसेट के केंद्र का विचलन है।
यह दर्शाने के लिए कि व्हीलसेट प्रक्षेपवक्र घुमावदार पथ का अनुसरण करता है, कोई व्यक्ति समतल टेबल टॉप पर कील या पेंच रख सकता है और उसे धक्का दे सकता है। यह वृत्ताकार वक्र में घूमेगा क्योंकि कील या पेंच अत्यधिक भिन्न-भिन्न व्यास वाले पहियों वाले व्हीलसेट की तरह है। हेड बड़े व्यास के पहिये के समान है और नुकीला सिरा छोटे व्यास के पहिये के समान है। जबकि कील या पेंच पूर्ण चक्र (और अधिक) में घूमेगा, रेलरोड व्हीलसेट भिन्न तरह से व्यवहार करता है क्योंकि जैसे ही यह वक्र में मुड़ना प्रारंभ करता है, प्रभावी व्यास इस तरह से परिवर्तित होजाते हैं कि पथ की वक्रता कम हो जाती है। ध्यान दें कि त्रिज्या और वक्रता व्हीलसेट के प्रक्षेप पथ की वक्रता को संदर्भित करती है, न कि रेलवे की वक्रता को क्योंकि यह सम्पूर्ण रूप में सीधा ट्रैक है। जैसे-जैसे पहिया आगे बढ़ता है, वक्रता कम हो जाती है जब तक कि पहिये उस बिंदु तक नहीं पहुंच जाते जहां उनके प्रभावी व्यास समान होते हैं और पथ अब घुमावदार नहीं होता है। किंतु प्रक्षेपवक्र में इस बिंदु पर स्लोप है (यह सीधी रेखा है जो ट्रैक की केंद्र रेखा को तिरछे पार करती है) जिससे यह ट्रैक की केंद्र रेखा से आगे निकल जाए और प्रभावी व्यास उलट जाता है (पहले छोटा व्यास वाला पहिया बड़ा व्यास और इसके विपरीत बन जाता है)। इसका परिणाम यह होता है कि पहिया विपरीत दिशा में वक्र में घूमने लगता है। यह फिर से केंद्र रेखा से आगे निकल जाता है और यह घटना पहिये के निकट से दोलन के साथ अनिश्चित काल तक जारी रहती है। ध्यान दें कि व्हील फ्लैंज कभी भी रेल से संपर्क नहीं बनाता है। इस मॉडल में, रेल को सदैव रेल हेड पर ही लाइन के साथ व्हील ट्रेड से संपर्क करने के लिए माना जाता है, जो मानता है कि रेल चाकू की धार वाली हैं और केवल लाइन (शून्य चौड़ाई) के साथ व्हील ट्रेड के साथ संपर्क बनाती हैं।
गणितीय विश्लेषण
पहिए के टायर के शंक्वाकार आकार के कारण ट्रेन पटरी पर टिकी रहती है। यदि व्हीलसेट को y (ट्रैकिंग त्रुटि) द्वारा एक तरफ से कुछ मात्रा में विस्थापित किया जाता है, तो एक तरफ रेल के संपर्क में चलने की त्रिज्या कम हो जाती है, जबकि दूसरी तरफ बढ़ जाती है। कोणीय वेग दोनों पहियों के लिए समान है (वे कठोरता धुरी के माध्यम से जुड़े हुए हैं), इसलिए बड़े व्यास वाले चलने की गति तेज हो जाती है, जबकि छोटे व्यास वाले की गति धीमी हो जाती है। व्हील सेट रेल पर पहियों के साथ संपर्क के बिंदुओं और व्हील सेट की धुरी से निकलने वाले शंकु के जनरेटर के चौराहे द्वारा परिभाषित वक्रता के केंद्र के चारों ओर घूमता है। समरूप त्रिभुज को प्रयुक्त करने पर, हमें टर्न त्रिज्या प्राप्त होती है:
जहाँ d ट्रैक रेल गेज है, सीधे चलने पर पहिए की त्रिज्या r और k ट्रेड मशीन टेपर है (जो ट्रैक के लंबवत क्षैतिज दिशा में ट्रेड का स्लोप है)।
सीधे ट्रैक के सापेक्ष पहिये का पथ फलन y(x) द्वारा परिभाषित किया गया है, जहाँ x ट्रैक पर प्रगति है। इसे कभी-कभी ट्रैकिंग त्रुटि भी कहा जाता है।[3] परंतु गति की दिशा कमोबेश रेल के समानांतर (ज्यामिति) बनी रहे, पथ की वक्रता लगभग ट्रैक के साथ दूरी के संबंध में y के दूसरे व्युत्पन्न से संबंधित हो सकती है [4]
यह इस प्रकार है कि ट्रैक के साथ प्रक्षेपवक्र समीकरण द्वारा नियंत्रित होता है:[5]
यह तरंग दैर्ध्य वाली सरल हार्मोनिक गति है:
इस गतिक विश्लेषण से पता चलता है कि रेलगाड़ियाँ हर समय एक ओर से दूसरी ओर घूमती रहती हैं। वास्तव में, यह दोलन महत्वपूर्ण गति से नीचे डंपिंग अनुपात है और सवारी तदनुसार अधिक आरामदायक है। गतिज परिणाम गति उत्पन्न करने वाली शक्तियों की उपेक्षा करता है। इनका विश्लेषण क्रीप (गैर-रैखिक) की अवधारणा का उपयोग करके किया जा सकता है, किंतु इन्हें सरलता से मापना कुछ सीमा तक सम्मिश्र है, क्योंकि वे संपर्क के क्षेत्रों में पहिया और रेल के हर्ट्ज़ियन संपर्क तनाव से उत्पन्न होते हैं। ये घर्षण संपर्क यांत्रिकी के विषय हैं; हंटिंग गति विश्लेषण में इन प्रभावों को सम्मिलित करने वाली प्रारंभिक प्रस्तुति कार्टर द्वारा प्रस्तुत की गई थी।[7] ऐतिहासिक अवलोकन के लिए नॉथे देखें।[8]
यदि गति अधिक सीमा तक रेल के समानांतर है, तो व्हील सेट का कोणीय विस्थापन इस प्रकार दिया जाता है:
इस तरह:
कोणीय विक्षेपण भी सरल हार्मोनिक गति का अनुसरण करता है, जो चक्र के एक चौथाई तक निकट की गति से पीछे रहता है। विभिन्न प्रणालियों में, जिनमें दो भिन्न-भिन्न अवस्थाओं (इस स्थितियों में एक्सल यॉ विक्षेपण और पार्श्व विस्थापन) से युक्त हार्मोनिक गति की विशेषता होती है, दो गतियों के मध्य का चौथाई चक्र अंतराल प्रणाली को आगे की गति से ऊर्जा निकालने की क्षमता प्रदान करता है। यह प्रभाव विमान के पंखों के कंपन और सड़क वाहनों की गति के डगमगाने के साथ-साथ रेलवे वाहनों के हंटिंग में भी देखा जाता है। ऊपर प्राप्त गतिक समाधान क्रांतिक गति पर गति का वर्णन करता है।
व्यवहार में, क्रांतिक गति से नीचे, दो गतियों के मध्य अंतराल एक चौथाई चक्र से कम होता है जिससे गति कम हो जाती है, किंतु, महत्वपूर्ण गति से ऊपर, अंतराल एक चौथाई चक्र से अधिक होता है जिससे गति बढ़ जाती है।
जड़त्वीय बलों का अनुमान लगाने के लिए, दूरी व्युत्पन्न को समय व्युत्पन्न के रूप में व्यक्त करना आवश्यक है। यह वाहन की गति U का उपयोग करके किया जाता है, जिसे स्थिर माना जाता है:
यॉ में धुरी का कोणीय त्वरण है:
जड़त्व क्षण (जाइरोस्कोपिक प्रभाव की अनदेखी) है:
जहाँ F रेल के साथ कार्य करने वाला बल है और C व्हील सेट की जड़ता का क्षण है।
पहिये और रेल के मध्य अधिकतम घर्षण बल निम्न द्वारा दिया जाता है:
जहाँ W एक्सल लोड है और घर्षण का गुणांक है। निम्नलिखित द्वारा दी गई गति और धुरी विक्षेपण के संयोजन पर ग्रॉस फिसलन होगी:
यह अभिव्यक्ति महत्वपूर्ण गति का महत्वपूर्ण अधिक अनुमान देती है, किंतु यह उस भौतिक कारण को स्पष्ट करती है कि हंटिंग क्यों होता है, अर्थात जड़त्वीय बल निश्चित गति से ऊपर आसंजन बलों के साथ तुलनीय हो जाते हैं। इस स्थितियों में घर्षण को सीमित करना आसंजन बल का खराब प्रतिनिधित्व है।
वास्तविक आसंजन बल संपर्क के क्षेत्र में ट्रेड और रेल की विकृति से उत्पन्न होते हैं। कोई स्थूल फिसलन नहीं है, केवल लोचदार विकृति और कुछ स्थानीय फिसलन (क्रीप फिसलन) है। सामान्य ऑपरेशन के समय ये बल सीमित घर्षण बाधा के अन्दर होते हैं। घर्षण संपर्क यांत्रिकी सिद्धांतों का उपयोग करते हुए संपूर्ण विश्लेषण इन बलों को ध्यान में रखता है।
चूँकि, गतिक विश्लेषण ने माना कि व्हील-रेल संपर्क में सम्पूर्ण रूप में भी फिसलन नहीं थी। अब यह स्पष्ट है कि कुछ रेंगने वाली फिसलन है जो व्हीलसेट के परिकलित साइनसॉइडल प्रक्षेपवक्र (क्लिंगल के सूत्र के अनुसार) को सम्पूर्ण रूप में सही नहीं बनाती है।
ऊर्जा संतुलन
क्रांतिक गति का अनुमान प्राप्त करने के लिए, हम इस तथ्य का उपयोग करते हैं कि जिस स्थिति के लिए यह गतिज समाधान वैध है वह उस स्थिति से मेल खाती है जहां परिवेश के साथ कोई शुद्ध ऊर्जा विनिमय नहीं होता है, इसलिए गतिज ऊर्जा और संभावित ऊर्जा पर विचार करके प्रणाली, हमें महत्वपूर्ण गति प्राप्त करने में सक्षम होना चाहिए।
माना:
ऑपरेटर का उपयोग करना:
कोणीय त्वरण समीकरण को यव में कोणीय वेग के संदर्भ में व्यक्त किया जा सकता है, :
एकीकृत करना:
अतः घूर्णन के कारण गतिज ऊर्जा है:
जब धुरी पीछे हटती है, तो संपर्क के बिंदु ट्रेडों पर बाहर की ओर चले जाते हैं जिससे धुरी की ऊंचाई कम हो जाती है। समर्थन बिंदुओं के बीच की दूरी बढ़ जाती है:
(छोटी मात्रा के दूसरे क्रम तक) ट्रेडों के केंद्रों से समर्थन बिंदु का विस्थापन है:
एक्सल लोड कम हो जाता है
एक्सल लोड को कम करके किया गया कार्य इस प्रकार है:
यह प्रणाली से लुप्त ऊर्जा है, इसलिए गति जारी रखने के लिए, व्हीलसेट की आगे की गति से समान मात्रा में ऊर्जा निकाली जानी चाहिए।
बाहरी पहिये का वेग निम्न द्वारा दिया गया है:
गतिज ऊर्जा है:
आंतरिक पहिये के लिए यह है
कहाँ m दोनों पहियों का द्रव्यमान है।
गतिज ऊर्जा में वृद्धि है:
गति निरंतर आयाम पर तब तक जारी रहेगी जब तक आगे की गति से निकाली गई ऊर्जा, और शून्य यॉ पर सेट किए गए पहिये की बढ़ी हुई गतिज ऊर्जा के रूप में प्रकट होती है, अधिकतम यॉ पर धुरी भार को कम करने से लुप्त संभावित ऊर्जा के समान है .
अब, किनेमेटिक्स से:
किंतु
अनुवादात्मक गतिज ऊर्जा है
कुल गतिज ऊर्जा है:
क्रांतिक गति ऊर्जा संतुलन से पाई जाती है:
अतः क्रांतिक गति किसके द्वारा दी गई है?
यह व्हील टेपर से स्वतंत्र है, किंतु एक्सल संरचनात्मक भार और व्हील सेट द्रव्यमान के अनुपात पर निर्भर करता है। यदि धागों का आकार वास्तव में शंक्वाकार होता, तो क्रांतिक गति टेपर से स्वतंत्र होती। व्यवहार में, पहिये पर घिसाव के कारण टेपर चलने की चौड़ाई में भिन्न होता है, जिससे संभावित ऊर्जा निर्धारित करने के लिए उपयोग किए जाने वाले टेपर का मूल्य गतिज ऊर्जा की गणना करने के लिए उपयोग किए जाने वाले से भिन्न होता है। पूर्व को इस रूप में निरूपित करना a, क्रांतिक गति बन जाती है:
कहाँ a अब पहिए की घिसावट से निर्धारित होने वाला आकार कारक है। यह परिणाम विकेंस (1965) में प्राप्त हुआ है [9] मानक नियंत्रण इंजीनियरिंग विधियों का उपयोग करके प्रणाली गतिशीलता के विश्लेषण से किया जाता है।
सरलीकृत विश्लेषण की सीमा
इस विश्लेषण से पता चलता है कि व्हील सेट की गति कहीं अधिक सम्मिश्र है। वाहन के निलंबन द्वारा अतिरिक्त निरोधक बल लगाए जाते हैं [10] और, उच्च गति पर, व्हील सेट अतिरिक्त जाइरोस्कोपिक टॉर्क उत्पन्न करेगा, जो महत्वपूर्ण गति के अनुमान को संशोधित करेगा। परंपरागत रूप से रेलवे वाहन कम गति में स्थिर गति रखता है, जब यह उच्च गति तक पहुंचता है तो स्थिरता अस्थिर रूप में परिवर्तित होजाती है। रेल वाहन प्रणाली की गतिशीलता के गैर-रेखीय विश्लेषण का मुख्य उद्देश्य स्पर्शरेखा ट्रैक में रेल वाहनों के द्विभाजन, गैर-रेखीय पार्श्व स्थिरता और हंटिंग व्यवहार की विश्लेषणात्मक जांच का दृश्य दिखाना है। यह अध्ययन विश्लेषण के लिए बोगोलीउबोव विधि का वर्णन करता है।[11] दो मुख्य स्थिति, अर्थात् निकाय को निश्चित समर्थन के रूप में मानना और हंटिंग की गति की गणना में गैर-रेखीय तत्वों का प्रभाव, अधिकतर अध्ययनों में केंद्रित हैं।[12] वास्तविक रेलवे वाहन में स्वतंत्रता की विभिन्न और डिग्री होती हैं और परिणामस्वरूप, एक से अधिक महत्वपूर्ण गति हो सकती है; यह किसी भी तरह से निश्चित नहीं है कि निम्नतम पहिए की गति से स्थिर होता है। चूँकि, विश्लेषण शिक्षाप्रद है क्योंकि यह दिखाता है कि हंटिंग क्यों होता है। जैसे-जैसे गति बढ़ती है, जड़त्वीय बल आसंजन बलों के साथ तुलनीय हो जाते हैं। इसीलिए महत्वपूर्ण गति धुरी भार (जो आसंजन बल निर्धारित करती है) और व्हीलसेट द्रव्यमान (जो जड़त्व बल निर्धारित करती है) के अनुपात पर निर्भर करती है।
वैकल्पिक रूप से, निश्चित गति से नीचे, आगे की गति से जो ऊर्जा निकाली जाती है, वह धुरियों को नीचे करने से लुप्त ऊर्जा को बदलने के लिए अपर्याप्त होती है और गति नम हो जाती है; इस गति से ऊपर, निकाली गई ऊर्जा संभावित ऊर्जा में हानि से अधिक होती है और आयाम बनता है।
अधिकतम एक्सल यॉ पर संभावित ऊर्जा को एक्सल की यॉ गति पर लोचदार बाधा को सम्मिलित करके बढ़ाया जा सकता है, जिससे स्प्रिंग तनाव से उत्पन्न होने वाला योगदान हो। पहियों की यॉ गति पर बाधा को बढ़ाने के लिए बोगियों में पहियों की व्यवस्था करना और बोगी में लोचदार बाधाओं को प्रयुक्त करने से भी महत्वपूर्ण गति बढ़ जाती है। समीकरण में लोचदार बलों का परिचय निलंबन डिजाइनों की अनुमति देता है जो मौलिक हंटिंग के अतिरिक्त केवल सकल फिसलन की प्रारंभ तक सीमित होते हैं। हंटिंग के आभासी उन्मूलन के लिए भुगतान किया जाने वाला जुर्माना सीधा रास्ता है, जिसमें रास्ते के अधिकार की समस्या और विरासत के सम्मिश्र प्रारूप के साथ असंगतता सम्मिलित है।
हंटिंग गतिशील समस्या है जिसे कम से कम सैद्धांतिक रूप से सक्रिय फीडबैक नियंत्रण द्वारा हल किया जा सकता है, जिसे ट्रैक की गुणवत्ता के अनुसार अनुकूलित किया जा सकता है। चूँकि, सक्रिय नियंत्रण की प्रारंभ विश्वसनीयता और सुरक्षा के उद्देश्यों को उठाती है।
हंटिंग प्रारंभ होने के कुछ ही समय पश्चात, भारी फिसलन होती है और पहिए के फ्लैंज पटरियों पर प्रभाव डालते हैं, जिससे संभावित रूप से दोनों को हानि होता है।
सड़क-रेल वाहन
विभिन्न सड़क-रेल वाहनों में प्रत्येक रेल पहिये पर स्वतंत्र धुरी और निलंबन प्रणाली होती है। जब इसे रेल पर सड़क पहियों की उपस्थिति के साथ जोड़ा जाता है तो उपरोक्त सूत्रों का उपयोग करना सम्मिश्र हो जाता है। ऐतिहासिक रूप से, सड़क-रेल वाहनों के अगले पहिये थोड़े-से अंदर की ओर सेट होते हैं, जिससे वाहन को रेल पर चलाते समय हंटिंग को कम करने में सहायता मिलती है।
यह भी देखें
- घर्षणात्मक संपर्क यांत्रिकी
- रेल आसंजन
- रेल प्रोफ़ाइल
- गति का वोबल
- वाहन की गतिशीलता
- व्हीलसेट (रेल परिवहन)
इस वर्ग की समस्या से सामना करने के सामान्य विधियों के लिए देखें
- नियंत्रण इंजीनियरिंग
संदर्भ
- ↑ 1.0 1.1 1.2 Oxford English Dictionary (2nd ed.). Oxford University Press. 1989.
f. The action of a machine, instrument, system, etc., that is hunting (see hunt v. 7b); an undesirable oscillation about an equilibrium speed, position, or state.
- ↑ https://www.talgo.com/en/rolling-stock/very-high-speed/350/
- ↑ Tracking error will be zero if the path of the wheels runs absolutely straight along the track and the wheel pair is centered on the track.
- ↑ See Curvature#Graph of a function for mathematical details. The approximate equality becomes equality only when the tracking error, y, has zero slope with respect to x. Since the tracking error will turn out to be a sine wave, the points of zero slope are at the points of maximum tracking error y. But the equality is approximately correct provided the slope of y is low.
- ↑ Note that is negative when y is positive and conversely. The other equation for R, does not hold when y goes negative, since the radius R is not allowed to be negative (per mathematical definition). But after radius R is eliminated by combining the two equations, the resulting equation becomes correct by checking the two cases: y negative and y positive.
- ↑ Iwnicki, p.7 formula 2.1
- ↑ Carter, F. W. (July 25, 1928). "लोकोमोटिव के संचालन की स्थिरता पर". Proceedings of the Royal Society. A. 121 (788): 585–610. Bibcode:1928RSPSA.121..585C. doi:10.1098/rspa.1928.0220.
- ↑ Knothe, K. (2008). "History of wheel/rail contact mechanics: from Redtenbacher to Kalker". Vehicle System Dynamics. 46 (1–2): 9–26. doi:10.1080/00423110701586469. S2CID 109580328.
- ↑ Wickens, A. H. (1965–66). "The Dynamics of Railway Vehicles on Straight Track: Fundamental Considerations of Lateral Stability". Proceedings of the Institution of Mechanical Engineers: 29–.
- ↑ Wickens, A. H.; Gilchrist, A. O.; Hobbs, A. E. W. (1969–70). "उच्च प्रदर्शन वाले दो-एक्सल मालवाहक वाहनों के लिए सस्पेंशन डिज़ाइन". Proceedings of the Institution of Mechanical Engineers: 22–.
- ↑ Serajian, Reza (2013). "एक बोगी के शिकार व्यवहार के गैर-रेखीय विश्लेषण पर विभिन्न पार्श्व कठोरता के साथ पैरामीटर्स का बदलता प्रभाव". Journal of Measurements in Engineering: 195–206.
- ↑ Serajian, Reza (2011). "हॉपफ द्विभाजन सिद्धांत द्वारा मान्यता प्राप्त नॉनलाइनियर व्हील-सेट शिकार पर बोगी और शरीर की जड़ता का प्रभाव". Int J Auto Engng: 186–196.
- Iwnicki, Simon (2006). Handbook of railway vehicle dynamics. CRC Press.
- Shabana, Ahmed A.; et al. (2008). Railroad vehicle dynamics : a computational approach. CRC Press.
- Wickens, A H (Jan 1, 2003). Fundamentals of rail vehicle dynamics : guidance and lateral stability. Swets & Zeitlinger.
- Serajian, Reza (2013). Parameters' changing influence with different lateral stiffnesses on nonlinear analysis of hunting behavior of a bogie. CRC Press.
- Serajian, Reza (2011). Effects of the bogie and body inertia on the nonlinear wheel-set hunting recognized by the hopf bifurcation theory. CRC Press.