समपूरक जाली: Difference between revisions
(Created page with "File:Fano plane Hasse diagram.svg|thumb|एक पूरक जालक का हास आरेख। एक बिंदु {{mvar|p}} और एक पंक्ति...") |
No edit summary |
||
| (12 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
[[File:Fano plane Hasse diagram.svg|thumb| | [[File:Fano plane Hasse diagram.svg|thumb| पूरक जालक का हास आरेख। एक बिंदु {{mvar|p}} और पंक्ति फैनो विमान के } पूरक हैं यदि और केवल यदि {{mvar|p}} झूठ नहीं बोलता {{mvar|l}}.]][[आदेश सिद्धांत|ऑर्डर सिद्धांत]] के गणित अनुशासन में, पूरक जालक बंधी हुई जालक (क्रम) है | ([[कम से कम तत्व]] 0 और [[सबसे बड़ा तत्व]] 1), जिसमें प्रत्येक तत्व ''a'' का पूरक है | अर्थात तत्व ''b'' ''a'' ∨ ''b'' = 1 और ''a'' ∧ ''b'' = 0 है । | ||
पूरक अद्वितीय नहीं होना चाहिए। | पूरक अद्वितीय नहीं होना चाहिए। | ||
अपेक्षाकृत पूरक जालक एक जालक है | जैसे कि प्रत्येक [[अंतराल (आंशिक क्रम)]] [''c'', ''d''], जिसे अपने आप में बंधी हुई जालक के रूप में देखा जाता है | पूरक जालक है। | |||
पूरक जालक पर ऑर्थोकोम्प्लीमेंटेशन [[इनवोल्यूशन (गणित)]] है | जो [[ क्रम उलटना |क्रम उलटना]] है और प्रत्येक तत्व को पूरक के रूप में मैप करता है। [[मॉड्यूलर जाली|मॉड्यूलर जालक]] के अशक्त रूप को संतुष्ट करने वाली ऑर्थोकोम्प्लीमेंटेड जालक को ऑर्थोमॉड्यूलर जालक कहा जाता है। | |||
परिबद्ध वितरण जालक में, पूरक अद्वितीय होते हैं। प्रत्येक पूरक [[वितरण जाली]] में | परिबद्ध वितरण जालक में, पूरक अद्वितीय होते हैं। प्रत्येक पूरक [[वितरण जाली|वितरण जालक]] में अद्वितीय ऑर्थोकोम्प्लिमेंटेशन होता है और वास्तव में [[बूलियन बीजगणित (संरचना)]] है। | ||
== परिभाषा और | == परिभाषा और मूलभूत गुण == | ||
पूरक जालक बंधी हुई जालक है | (कम से कम तत्व 0 और सबसे बड़ा तत्व 1 के साथ), जिसमें प्रत्येक तत्व ''a'' का पूरक है, अर्थात तत्व ''b'' ऐसा है कि | |||
::''a'' ∨ ''b'' = 1 and ''a'' ∧ ''b'' = 0। | ::''a'' ∨ ''b'' = 1 and ''a'' ∧ ''b'' = 0। | ||
सामान्यतः तत्व में एक से अधिक पूरक हो सकते हैं। चूँकि, वितरण जालक में प्रत्येक तत्व में अधिकतम पूरक होगा।<ref>Grätzer (1971), Lemma I.6.1, p. 47. Rutherford (1965), Theorem 9.3 p. 25.</ref> जालक जिसमें प्रत्येक तत्व का सही पूरक होता है | विशिष्ट पूरक जालक कहलाता है | <ref>{{citation|title=Semimodular Lattices: Theory and Applications|series=Encyclopedia of Mathematics and its Applications|first=Manfred|last=Stern|publisher=Cambridge University Press|year=1999|isbn=9780521461054|page=29|url=https://books.google.com/books?id=VVYd2sC19ogC&pg=PA29}}.</ref> संपत्ति के साथ जालक जिसे प्रत्येक अंतराल ( उप-जाल के रूप में देखा जाता है) को पूरक किया जाता है | उसे अपेक्षाकृत पूरक जालक कहा जाता है। दूसरे शब्दों में, अपेक्षाकृत पूरक जालक की संपत्ति की विशेषता होती है कि अंतराल में प्रत्येक तत्व ''a'' के लिए ['' c '', ''d ''] तत्व ''b'' होता है | | |||
संपत्ति के साथ | |||
::''a'' ∨ ''b'' = ''d'' and ''a'' ∧ ''b'' = ''c''। | ::''a'' ∨ ''b'' = ''d'' and ''a'' ∧ ''b'' = ''c''। | ||
ऐसे तत्व '' | ऐसे तत्व ''b'' को अंतराल के सापेक्ष ''a'' का पूरक कहा जाता है। | ||
वितरण जालक को पूरक किया जाता है | यदि और केवल यदि यह बाध्य और अपेक्षाकृत पूरक हो ।<ref>Grätzer (1971), Lemma I.6.2, p. 48. This result holds more generally for modular lattices, see Exercise 4, p. 50.</ref><ref>Birkhoff (1961), Corollary IX.1, p. 134</ref> सदिश स्थान के सदिश उपस्थानों की जालक पूरक जालक का प्रत्येक कण प्रदान करती है | जो सामान्य रूप से वितरण नहीं है। | |||
==ऑर्थोकंप्लीमेंटेशन== | ==ऑर्थोकंप्लीमेंटेशन== | ||
{{see also| | {{see also|डी मॉर्गन बीजगणित}} | ||
<gallery | बंधे हुए जालक पर ऑर्थोकोम्प्लिमेंटेशन ऐसा कार्य है | जो प्रत्येक तत्व ''a'' को ऑर्थोकोम्प्लीमेंट ''a<sup>⊥</sup>'' से मैप करता है। इस तरह से कि निम्नलिखित स्वयंसिद्ध संतुष्ट होंते है | <ref>{{harvtxt|Stern|1999}}, p. 11.</ref> | ||
पूरक नियम: | |||
''a''<sup>⊥</sup> ∨ ''a'' = 1 और ''a''<sup>⊥</sup> ∧ ''a'' = 0. | |||
इन्वोल्यूशन लॉ: | |||
''a''<sup>⊥⊥</sup> = ''a''. | |||
ऑर्डर-रिवर्सिंग: | |||
यदि ''a'' ≤ ''b'' तो ''b''<sup>⊥</sup> ≤ ''a''<sup>⊥</sup> | |||
ऑर्थोकम्प्लिमेंटेड लैटिस या ऑर्थोलैटिस बाउंडेड लैटिस है | जो ऑर्थोकोम्प्लिमेंटेशन से लैस है। [[आंतरिक उत्पाद स्थान]] के उप-स्थानों की जालक, और [[ऑर्थोगोनल पूरक]] संचालन, ऑर्थोकोम्प्लीमेंटेड जालक का उदाप्रत्येकण प्रदान करता है | जो सामान्य रूप से वितरण नहीं है।<sup><ref name=":0">[http://unapologetic.wordpress.com/2009/05/07/orthogonal-complements-and-the-lattice-of-subspaces/ The Unapologetic Mathematician: Orthogonal Complements and the Lattice of Subspaces].</ref> | |||
<gallery caption="Some complemented lattices"> | |||
Image:Smallest_nonmodular_lattice_1.svg|पेंटागन जाली में N<sub>5</sub>, दाईं ओर के नोड में दो पूरक हैं। | Image:Smallest_nonmodular_lattice_1.svg|पेंटागन जाली में N<sub>5</sub>, दाईं ओर के नोड में दो पूरक हैं। | ||
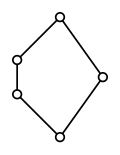
Image:Diamond lattice.svg|हीरा जाली एम<sub>3</sub> कोई orthocomplementation स्वीकार नहीं करता है। | Image:Diamond lattice.svg|हीरा जाली एम<sub>3</sub> कोई orthocomplementation स्वीकार नहीं करता है। | ||
| Line 35: | Line 43: | ||
Image:Hexagon lattice.svg|हेक्सागोन जाली एक अद्वितीय ऑर्थोकोम्प्लीमेंटेशन स्वीकार करती है, लेकिन यह विशिष्ट रूप से पूरक नहीं है। | Image:Hexagon lattice.svg|हेक्सागोन जाली एक अद्वितीय ऑर्थोकोम्प्लीमेंटेशन स्वीकार करती है, लेकिन यह विशिष्ट रूप से पूरक नहीं है। | ||
</gallery> | </gallery> | ||
बूलियन बीजगणित (संरचना) | बूलियन बीजगणित (संरचना) ऑर्थो कॉम्प्लिमेंटेड जालक की विशेष स्थिति है | जो बदले में पूरक जालक (अतिरिक्त संरचना के साथ) का विशेष स्थिति है। ऑर्थोलैटिस का उपयोग अधिकांशतः [[ क्वांटम तर्क |क्वांटम तर्क]] में किया जाता है | जहां पृथक स्थान [[ हिल्बर्ट अंतरिक्ष |हिल्बर्ट अंतरिक्ष]] के [[बंद सेट]] रेखीय उप-स्थान क्वांटम प्रस्तावों का प्रतिनिधित्व करते हैं और ऑर्थोकोम्प्लीमेंटेड जालक के रूप में व्यवहार करते हैं। | ||
ऑर्थोकम्प्लीमेंटेड लैटिस, जैसे बूलियन बीजगणित, मॉर्गन के नियमों को पूरा करते हैं | ऑर्थोकम्प्लीमेंटेड लैटिस, जैसे बूलियन बीजगणित, मॉर्गन के नियमों को पूरा करते हैं | | ||
* ( | ** (''a'' ∨ ''b'')<sup>⊥</sup> = ''a''<sup>⊥</sup> ∧ ''b''<sup>⊥</sup> | ||
* ( | ** (''a'' ∧ ''b'')<sup>⊥</sup> = ''a''<sup>⊥</sup> ∨ ''b''<sup>⊥</sup>. | ||
== ऑर्थोमॉड्यूलर लैटिस == | == ऑर्थोमॉड्यूलर लैटिस == | ||
जालक को मॉड्यूलर जालक कहा जाता है | यदि सभी तत्वों के लिए a, b और c सम्मिलित हैं | | |||
:: | ::यदि a ≤ c, तो a ∨ (b ∧ c) = (a ∨ b) ∧ c | ||
यह वितरणात्मक जालक से अशक्त है; उदाहरण. ऊपर दिखाया गया जालक m<sub>3</sub> मॉड्यूलर है | किन्तु वितरण नहीं है। | |||
क्वांटम लॉजिक में अनुप्रयोगों के लिए आवश्यक ऑर्थोकोम्प्लीमेंटेड लैटिस के लिए इस स्थिति का एक और अशक्त होना, केवल विशेष स्थिति b = a में इसकी आवश्यकता है | ऑर्थोमॉड्यूलर जालक को ऑर्थोकोम्प्लीमेंटेड जालक के रूप में परिभाषित किया गया है | जैसे कि किसी भी दो तत्वों के लिए सम्मिलित है | | |||
::यदि ''a'' ≤ ''c'', तो ''a'' ∨ (''a''<sup>⊥</sup> ∧ ''c'') = ''c'' | |||
क्वांटम लॉजिक के अध्ययन के लिए इस रूप के लैटिस महत्वपूर्ण हैं | क्योंकि वे [[क्वांटम यांत्रिकी]] के क्वांटम यांत्रिकी के हिल्बर्ट अंतरिक्ष गणितीय सूत्रीकरण के स्वयंसिद्ध का भाग हैं। [[गैरेट बिरखॉफ]] और [[जॉन वॉन न्यूमैन]] ने देखा कि क्वांटम तर्क में प्रस्तावन तर्क तार्किक कलन औपचारिक रूप से रैखिक सबस्पेस सम्स और ऑर्थोगोनल पूरक के संबंध में रैखिक उप-स्थानों हिल्बर्ट अंतरिक्ष की गणना से अप्रभेद्य है और, या की भूमिकाओं के अनुरूप है। और बूलियन लैटिस में नहीं। इस टिप्पणी ने हिल्बर्ट अंतरिक्ष के बंद उप-स्थानों में रुचि उत्पन्न की है | जो ऑर्थोमॉड्यूलर जालक बनाते हैं।<ref name="PadmanabhanRudeanu2008">{{cite book|author1=Ranganathan Padmanabhan|author2=Sergiu Rudeanu|title=जाली और बूलियन बीजगणित के लिए अभिगृहीत|url=https://books.google.com/books?id=JlXSlpmlSv4C&pg=PA128|year=2008|publisher=World Scientific|isbn=978-981-283-454-6|page=128}}</ref> | |||
== यह भी देखें == | == यह भी देखें == | ||
* [[छद्म पूरक जाली]] | * [[छद्म पूरक जाली|स्यूडोकंप्लीमेंटेड जालक]] | ||
==टिप्पणियाँ== | ==टिप्पणियाँ== | ||
| Line 69: | Line 74: | ||
== | ==बाप्रत्येकी संबंध== | ||
{| style="float:right" | {| style="float:right" | ||
| Line 80: | Line 85: | ||
{{Order theory}} | {{Order theory}} | ||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:Collapse templates]] | |||
[[Category:Created On 18/05/2023]] | [[Category:Created On 18/05/2023]] | ||
[[Category:Machine Translated Page]] | |||
[[Category:Navigational boxes| ]] | |||
[[Category:Navigational boxes without horizontal lists]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Sidebars with styles needing conversion]] | |||
[[Category:Template documentation pages|Documentation/doc]] | |||
[[Category:Templates Translated in Hindi]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates generating microformats]] | |||
[[Category:Templates that are not mobile friendly]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:Wikipedia metatemplates]] | |||
[[Category:जाली सिद्धांत]] | |||
Latest revision as of 14:06, 15 June 2023
ऑर्डर सिद्धांत के गणित अनुशासन में, पूरक जालक बंधी हुई जालक (क्रम) है | (कम से कम तत्व 0 और सबसे बड़ा तत्व 1), जिसमें प्रत्येक तत्व a का पूरक है | अर्थात तत्व b a ∨ b = 1 और a ∧ b = 0 है ।
पूरक अद्वितीय नहीं होना चाहिए।
अपेक्षाकृत पूरक जालक एक जालक है | जैसे कि प्रत्येक अंतराल (आंशिक क्रम) [c, d], जिसे अपने आप में बंधी हुई जालक के रूप में देखा जाता है | पूरक जालक है।
पूरक जालक पर ऑर्थोकोम्प्लीमेंटेशन इनवोल्यूशन (गणित) है | जो क्रम उलटना है और प्रत्येक तत्व को पूरक के रूप में मैप करता है। मॉड्यूलर जालक के अशक्त रूप को संतुष्ट करने वाली ऑर्थोकोम्प्लीमेंटेड जालक को ऑर्थोमॉड्यूलर जालक कहा जाता है।
परिबद्ध वितरण जालक में, पूरक अद्वितीय होते हैं। प्रत्येक पूरक वितरण जालक में अद्वितीय ऑर्थोकोम्प्लिमेंटेशन होता है और वास्तव में बूलियन बीजगणित (संरचना) है।
परिभाषा और मूलभूत गुण
पूरक जालक बंधी हुई जालक है | (कम से कम तत्व 0 और सबसे बड़ा तत्व 1 के साथ), जिसमें प्रत्येक तत्व a का पूरक है, अर्थात तत्व b ऐसा है कि
- a ∨ b = 1 and a ∧ b = 0।
सामान्यतः तत्व में एक से अधिक पूरक हो सकते हैं। चूँकि, वितरण जालक में प्रत्येक तत्व में अधिकतम पूरक होगा।[1] जालक जिसमें प्रत्येक तत्व का सही पूरक होता है | विशिष्ट पूरक जालक कहलाता है | [2] संपत्ति के साथ जालक जिसे प्रत्येक अंतराल ( उप-जाल के रूप में देखा जाता है) को पूरक किया जाता है | उसे अपेक्षाकृत पूरक जालक कहा जाता है। दूसरे शब्दों में, अपेक्षाकृत पूरक जालक की संपत्ति की विशेषता होती है कि अंतराल में प्रत्येक तत्व a के लिए [ c , d ] तत्व b होता है |
- a ∨ b = d and a ∧ b = c।
ऐसे तत्व b को अंतराल के सापेक्ष a का पूरक कहा जाता है।
वितरण जालक को पूरक किया जाता है | यदि और केवल यदि यह बाध्य और अपेक्षाकृत पूरक हो ।[3][4] सदिश स्थान के सदिश उपस्थानों की जालक पूरक जालक का प्रत्येक कण प्रदान करती है | जो सामान्य रूप से वितरण नहीं है।
ऑर्थोकंप्लीमेंटेशन
बंधे हुए जालक पर ऑर्थोकोम्प्लिमेंटेशन ऐसा कार्य है | जो प्रत्येक तत्व a को ऑर्थोकोम्प्लीमेंट a⊥ से मैप करता है। इस तरह से कि निम्नलिखित स्वयंसिद्ध संतुष्ट होंते है | [5]
पूरक नियम:
a⊥ ∨ a = 1 और a⊥ ∧ a = 0.
इन्वोल्यूशन लॉ:
a⊥⊥ = a.
ऑर्डर-रिवर्सिंग:
यदि a ≤ b तो b⊥ ≤ a⊥
ऑर्थोकम्प्लिमेंटेड लैटिस या ऑर्थोलैटिस बाउंडेड लैटिस है | जो ऑर्थोकोम्प्लिमेंटेशन से लैस है। आंतरिक उत्पाद स्थान के उप-स्थानों की जालक, और ऑर्थोगोनल पूरक संचालन, ऑर्थोकोम्प्लीमेंटेड जालक का उदाप्रत्येकण प्रदान करता है | जो सामान्य रूप से वितरण नहीं है।[6]
- Some complemented lattices
हीरा जाली एम3 कोई orthocomplementation स्वीकार नहीं करता है।
जाली एम4 3 orthocomplementations को स्वीकार करता है।
हेक्सागोन जाली एक अद्वितीय ऑर्थोकोम्प्लीमेंटेशन स्वीकार करती है, लेकिन यह विशिष्ट रूप से पूरक नहीं है।
बूलियन बीजगणित (संरचना) ऑर्थो कॉम्प्लिमेंटेड जालक की विशेष स्थिति है | जो बदले में पूरक जालक (अतिरिक्त संरचना के साथ) का विशेष स्थिति है। ऑर्थोलैटिस का उपयोग अधिकांशतः क्वांटम तर्क में किया जाता है | जहां पृथक स्थान हिल्बर्ट अंतरिक्ष के बंद सेट रेखीय उप-स्थान क्वांटम प्रस्तावों का प्रतिनिधित्व करते हैं और ऑर्थोकोम्प्लीमेंटेड जालक के रूप में व्यवहार करते हैं।
ऑर्थोकम्प्लीमेंटेड लैटिस, जैसे बूलियन बीजगणित, मॉर्गन के नियमों को पूरा करते हैं |
- (a ∨ b)⊥ = a⊥ ∧ b⊥
- (a ∧ b)⊥ = a⊥ ∨ b⊥.
ऑर्थोमॉड्यूलर लैटिस
जालक को मॉड्यूलर जालक कहा जाता है | यदि सभी तत्वों के लिए a, b और c सम्मिलित हैं |
- यदि a ≤ c, तो a ∨ (b ∧ c) = (a ∨ b) ∧ c
यह वितरणात्मक जालक से अशक्त है; उदाहरण. ऊपर दिखाया गया जालक m3 मॉड्यूलर है | किन्तु वितरण नहीं है।
क्वांटम लॉजिक में अनुप्रयोगों के लिए आवश्यक ऑर्थोकोम्प्लीमेंटेड लैटिस के लिए इस स्थिति का एक और अशक्त होना, केवल विशेष स्थिति b = a में इसकी आवश्यकता है | ऑर्थोमॉड्यूलर जालक को ऑर्थोकोम्प्लीमेंटेड जालक के रूप में परिभाषित किया गया है | जैसे कि किसी भी दो तत्वों के लिए सम्मिलित है |
- यदि a ≤ c, तो a ∨ (a⊥ ∧ c) = c
क्वांटम लॉजिक के अध्ययन के लिए इस रूप के लैटिस महत्वपूर्ण हैं | क्योंकि वे क्वांटम यांत्रिकी के क्वांटम यांत्रिकी के हिल्बर्ट अंतरिक्ष गणितीय सूत्रीकरण के स्वयंसिद्ध का भाग हैं। गैरेट बिरखॉफ और जॉन वॉन न्यूमैन ने देखा कि क्वांटम तर्क में प्रस्तावन तर्क तार्किक कलन औपचारिक रूप से रैखिक सबस्पेस सम्स और ऑर्थोगोनल पूरक के संबंध में रैखिक उप-स्थानों हिल्बर्ट अंतरिक्ष की गणना से अप्रभेद्य है और, या की भूमिकाओं के अनुरूप है। और बूलियन लैटिस में नहीं। इस टिप्पणी ने हिल्बर्ट अंतरिक्ष के बंद उप-स्थानों में रुचि उत्पन्न की है | जो ऑर्थोमॉड्यूलर जालक बनाते हैं।[7]
यह भी देखें
टिप्पणियाँ
- ↑ Grätzer (1971), Lemma I.6.1, p. 47. Rutherford (1965), Theorem 9.3 p. 25.
- ↑ Stern, Manfred (1999), Semimodular Lattices: Theory and Applications, Encyclopedia of Mathematics and its Applications, Cambridge University Press, p. 29, ISBN 9780521461054.
- ↑ Grätzer (1971), Lemma I.6.2, p. 48. This result holds more generally for modular lattices, see Exercise 4, p. 50.
- ↑ Birkhoff (1961), Corollary IX.1, p. 134
- ↑ Stern (1999), p. 11.
- ↑ The Unapologetic Mathematician: Orthogonal Complements and the Lattice of Subspaces.
- ↑ Ranganathan Padmanabhan; Sergiu Rudeanu (2008). जाली और बूलियन बीजगणित के लिए अभिगृहीत. World Scientific. p. 128. ISBN 978-981-283-454-6.
संदर्भ
- Birkhoff, Garrett (1961). Lattice Theory. American Mathematical Society.
- Grätzer, George (1971). Lattice Theory: First Concepts and Distributive Lattices. W. H. Freeman and Company. ISBN 978-0-7167-0442-3.
- Grätzer, George (1978). General Lattice Theory. Basel, Switzerland: Birkhäuser. ISBN 978-0-12-295750-5.
- Rutherford, Daniel Edwin (1965). Introduction to Lattice Theory. Oliver and Boyd.
बाप्रत्येकी संबंध
|