दोहरी पॉलीहेड्रॉन: Difference between revisions
No edit summary |
No edit summary |
||
| (3 intermediate revisions by 3 users not shown) | |||
| Line 21: | Line 21: | ||
रैखिक समीकरण द्वारा वर्णित <math>P</math> के प्रत्येक फलक के विमान के लिए | रैखिक समीकरण द्वारा वर्णित <math>P</math> के प्रत्येक फलक के विमान के लिए | ||
<math display="block">x_0x + y_0y + z_0z = r^2,</math> | <math display="block">x_0x + y_0y + z_0z = r^2,</math> | ||
द्वैत बहुफलक <math>P^\circ</math> का संगत शीर्ष निर्देशांक होंगे <math>(x_0,y_0,z_0)</math>. इसी प्रकार, प्रत्येक शीर्ष <math>P</math> के फलक <math>P^\circ</math> तल से मिलता है , और <math>P</math> प्रत्येक किनारे की रेखा की एक धार रेखा <math>P^\circ</math> से मिलता है . <math>P</math> तथा <math>P^\circ</math>के शीर्षों, किनारों और | द्वैत बहुफलक <math>P^\circ</math> का संगत शीर्ष निर्देशांक होंगे <math>(x_0,y_0,z_0)</math>. इसी प्रकार, प्रत्येक शीर्ष <math>P</math> के फलक <math>P^\circ</math> तल से मिलता है , और <math>P</math> प्रत्येक किनारे की रेखा की एक धार रेखा <math>P^\circ</math> से मिलता है . <math>P</math> तथा <math>P^\circ</math>के शीर्षों, किनारों और मुख के मध्य पत्राचार समावेशन को उलट देता है। उदाहरण के लिए, यदि <math>P</math> का एक किनारा एक शीर्ष, हैं <math>P^\circ</math> के संगत किनारे सम्मिलित संबंधित फलक में निहित होगा। | ||
समरूपता के केंद्र के साथ बहुफलक के लिए, इस बिंदु पर केंद्रित गोले का उपयोग करना सामान्य है, जैसा कि द्वैत वर्दी बहुफलक डोरमैन ल्यूक निर्माण (नीचे उल्लिखित) में है। विफल होने पर, बहुफलक के लिए सीमाबद्ध क्षेत्र, खुदा हुआ क्षेत्र, या मिडस्फीयर (स्पर्शरेखा के रूप में सभी किनारों के साथ), इसका उपयोग किया जा सकता है। चूंकि, किसी भी क्षेत्र के बारे में एक बहुफलक का आदान-प्रदान करना संभव है, और द्वैत का परिणामी रूप गोले के आकार और स्थिति पर निर्भर करेगा; जिस प्रकार क्षेत्र विविध है, उसी प्रकार द्वैत रूप भी है। गोले के केंद्र का चुनाव समानता तक द्वैत को परिभाषित करने के लिए पर्याप्त है। | समरूपता के केंद्र के साथ बहुफलक के लिए, इस बिंदु पर केंद्रित गोले का उपयोग करना सामान्य है, जैसा कि द्वैत वर्दी बहुफलक डोरमैन ल्यूक निर्माण (नीचे उल्लिखित) में है। विफल होने पर, बहुफलक के लिए सीमाबद्ध क्षेत्र, खुदा हुआ क्षेत्र, या मिडस्फीयर (स्पर्शरेखा के रूप में सभी किनारों के साथ), इसका उपयोग किया जा सकता है। चूंकि, किसी भी क्षेत्र के बारे में एक बहुफलक का आदान-प्रदान करना संभव है, और द्वैत का परिणामी रूप गोले के आकार और स्थिति पर निर्भर करेगा; जिस प्रकार क्षेत्र विविध है, उसी प्रकार द्वैत रूप भी है। गोले के केंद्र का चुनाव समानता तक द्वैत को परिभाषित करने के लिए पर्याप्त है। | ||
| Line 48: | Line 48: | ||
== स्व-द्वैत बहुफलक == | == स्व-द्वैत बहुफलक == | ||
स्थलाकृतिक रूप से, एक स्व-द्वैत बहुफलक वह है जिसके द्वैत में शीर्षों, किनारों और | स्थलाकृतिक रूप से, एक स्व-द्वैत बहुफलक वह है जिसके द्वैत में शीर्षों, किनारों और मुख के मध्य बिल्कुल समान संयोजकता होती है। संक्षेप में, उनके पास एक ही हस्स आरेख है। | ||
ज्यामितीय रूप से स्व-द्वैत बहुफलक न केवल स्थैतिक रूप से स्व-द्वैत है, किन्तु निश्चित बिंदु के बारे में इसका ध्रुवीय पारस्परिक, सामान्यतः इसका केन्द्रक, एक समान आकृति है। उदाहरण के लिए, एक नियमित चतुष्फलक का द्वैत एक अन्य नियमित चतुष्फलक है, मूल के माध्यम से प्रतिबिंब बना है। | ज्यामितीय रूप से स्व-द्वैत बहुफलक न केवल स्थैतिक रूप से स्व-द्वैत है, किन्तु निश्चित बिंदु के बारे में इसका ध्रुवीय पारस्परिक, सामान्यतः इसका केन्द्रक, एक समान आकृति है। उदाहरण के लिए, एक नियमित चतुष्फलक का द्वैत एक अन्य नियमित चतुष्फलक है, मूल के माध्यम से प्रतिबिंब बना है। | ||
| Line 56: | Line 56: | ||
इसी तरह, प्रत्येक टोपोलॉजिकल रूप से स्व-द्वैत उत्तल बहुफलक को समतुल्य ज्यामितीय रूप से स्व-द्वैत बहुफलक द्वारा अनुभव किया जा सकता है, इसके कैनोनिकल बहुफलक, मिडस्फीयर के केंद्र के बारे में पारस्परिक है। | इसी तरह, प्रत्येक टोपोलॉजिकल रूप से स्व-द्वैत उत्तल बहुफलक को समतुल्य ज्यामितीय रूप से स्व-द्वैत बहुफलक द्वारा अनुभव किया जा सकता है, इसके कैनोनिकल बहुफलक, मिडस्फीयर के केंद्र के बारे में पारस्परिक है। | ||
सामान्यतः कई ज्यामितीय स्व-द्वैत बहुफलक हैं। सबसे सरल अनंत | सामान्यतः कई ज्यामितीय स्व-द्वैत बहुफलक हैं। सबसे सरल अनंत वर्ग 'एन' पक्षों के विहित [[पिरामिड (ज्यामिति)]] हैं। एक अन्य अनंत वर्ग, [[लम्बी पिरामिड]], में बहुफलक होते हैं जिन्हें सामान्यतः [[प्रिज्म (ज्यामिति)]] के शीर्ष पर बैठे पिरामिड के रूप में वर्णित किया जा सकता है (समान संख्या में पक्षों के साथ)। प्रिज्म के नीचे एक छिन्नक (पिरामिड जिसका शीर्ष कटा हुआ है) जोड़ने से एक और अनंत वर्ग उत्पन्न होता है, और इसी तरह आगे भी उत्पन्न होता है। | ||
कई अन्य उत्तल, स्व-द्वैत बहुफलक हैं। उदाहरण के लिए, 7 शीर्षों के साथ 6 भिन्न हैं, और 8 शीर्षों के साथ 16 हैं।<ref>3D [[Java (programming language)|Java]] models at [http://dmccooey.com/polyhedra/SymmetricSelfDuals.html Symmetries of Canonical Self-Dual Polyhedra], based on paper by Gunnar Brinkmann, Brendan D. McKay, ''Fast generation of planar graphs'' [[PDF]] [http://cs.anu.edu.au/~bdm/papers/plantri-full.pdf]</ref> | कई अन्य उत्तल, स्व-द्वैत बहुफलक हैं। उदाहरण के लिए, 7 शीर्षों के साथ 6 भिन्न हैं, और 8 शीर्षों के साथ 16 हैं।<ref>3D [[Java (programming language)|Java]] models at [http://dmccooey.com/polyhedra/SymmetricSelfDuals.html Symmetries of Canonical Self-Dual Polyhedra], based on paper by Gunnar Brinkmann, Brendan D. McKay, ''Fast generation of planar graphs'' [[PDF]] [http://cs.anu.edu.au/~bdm/papers/plantri-full.pdf]</ref> | ||
1900 में ब्रुकनर द्वारा हेक्सागोनल | 1900 में ब्रुकनर द्वारा हेक्सागोनल मुख के साथ एक स्व-द्वैत गैर-उत्तल आईकोसाहेड्रॉन की पहचान की गई थी। <ref>Anthony M. Cutler and Egon Schulte; "Regular Polyhedra of Index Two", I; ''Beiträge zur Algebra und Geometrie'' / ''Contributions to Algebra and Geometry'' April 2011, Volume 52, Issue 1, pp 133–161.</ref><ref>N. J. Bridge; "Faceting the Dodecahedron", ''Acta Crystallographica'', Vol. A 30, Part 4 July 1974, Fig. 3c and accompanying text.</ref><ref>Brückner, M.; ''Vielecke und Vielflache: Theorie und Geschichte'', Teubner, Leipzig, 1900.</ref> गैर-उत्तल बहुफलक और उनके द्वैत की कुछ परिभाषाओं के अनुसार अन्य गैर-उत्तल स्व-द्वैत बहुफलक पाए गए हैं। | ||
{| class=wikitable | {| class=wikitable | ||
|+ [[Pyramid (geometry)|पिरामिड का | |+ [[Pyramid (geometry)|पिरामिड का वर्ग]] | ||
|- align=center | |- align=center | ||
|[[Image:Tetrahedron.jpg|100px]]<BR>[[Tetrahedron|3]] | |[[Image:Tetrahedron.jpg|100px]]<BR>[[Tetrahedron|3]] | ||
| Line 72: | Line 72: | ||
{| class=wikitable | {| class=wikitable | ||
|+ लम्बी पिरामिडों का | |+ लम्बी पिरामिडों का वर्ग | ||
|- align=center | |- align=center | ||
|[[Image:Elongated triangular pyramid.png|100px]]<BR>[[Elongated triangular pyramid|3]] | |[[Image:Elongated triangular pyramid.png|100px]]<BR>[[Elongated triangular pyramid|3]] | ||
| Line 80: | Line 80: | ||
{| class="wikitable" | {| class="wikitable" | ||
|+ डिमेस्ड ट्रेपोजोहेड्रा का | |+ डिमेस्ड ट्रेपोजोहेड्रा का वर्ग | ||
|- align=center | |- align=center | ||
| [[Image:Diminished trigonal trapezohedron.png|80px]]<BR>3 | | [[Image:Diminished trigonal trapezohedron.png|80px]]<BR>3 | ||
| Line 211: | Line 211: | ||
* {{mathworld | urlname = Self-DualPolyhedron | title = Self-dual polyhedron | mode=cs2}} | * {{mathworld | urlname = Self-DualPolyhedron | title = Self-dual polyhedron | mode=cs2}} | ||
{{DEFAULTSORT:Dual Polyhedron}}[[Category: | {{DEFAULTSORT:Dual Polyhedron}} | ||
[[Category:Articles with hatnote templates targeting a nonexistent page|Dual Polyhedron]] | |||
[[Category:Created On 27/11/2022|Dual Polyhedron]] | |||
[[Category:Lua-based templates|Dual Polyhedron]] | |||
[[Category:Machine Translated Page|Dual Polyhedron]] | |||
[[Category:Pages with script errors|Dual Polyhedron]] | |||
[[Category:Templates Vigyan Ready|Dual Polyhedron]] | |||
[[Category:Templates that add a tracking category|Dual Polyhedron]] | |||
[[Category:Templates that generate short descriptions|Dual Polyhedron]] | |||
[[Category:Templates using TemplateData|Dual Polyhedron]] | |||
[[Category:द्वैत सिद्धांत|बहुफलक]] | [[Category:द्वैत सिद्धांत|बहुफलक]] | ||
[[Category:पॉलीटॉप्स|Dual Polyhedron]] | |||
[[Category:पॉलीहेड्रा|Dual Polyhedron]] | |||
[[Category:स्वयं-द्वैत पॉलीहेड्रा| ]] | [[Category:स्वयं-द्वैत पॉलीहेड्रा| ]] | ||
Latest revision as of 09:57, 17 May 2023

ज्यामिति में, प्रत्येक बहुफलक एक दूसरी द्वैत संरचना से जुड़ा होता है, जहां एक का शीर्ष (ज्यामिति) दूसरे के फलक (ज्यामिति) के अनुरूप होता है, और एक के शीर्षों के जोड़े के मध्य के जोड़े के किनारों के अनुरूप होते हैं। [1] इस तरह के द्वैत आंकड़े संयोजी या अमूर्त पॉलीटॉप रहते हैं, किन्तु सभी को ज्यामितीय बहुफलक के रूप में भी नहीं बनाया जा सकता है।[2] किसी दिए गए बहुफलक से प्रारंभ करके, इसके द्वैत का द्वैत मूल बहुफलक है।
द्वैत बहुफलकी की समरूपता को बनाए रखता है। इसलिए, उनकी समरूपता द्वारा परिभाषित बहुफलक के कई वर्गों के लिए, द्वैत संबंधित समरूपता वर्ग से संबंधित हैं। उदाहरण के लिए, नियमित बहुफलक(उत्तल) प्लेटोनिक ठोस और (तारा) केप्लर-पॉइन्सॉट बहुफलक द्वैत जोड़े बनाते हैं, जहां नियमित बहुफलक स्व-द्वैत है। आइसोगोनल आकृति बहुफलक का द्वैत (जिसमें कोई भी दो कोने बहुफलक की समरूपता के समान हैं) एक आइसोहेड्रल आकृति बहुफलक है (जिसमें कोई भी दो फलक समकक्ष हैं और इसके विपरीत आइसोटॉक्सल आंकड़ा बहुफलक का द्वैत (जिसमें कोई भी दो किनारे समतुल्य हैं) भी आइसोटॉक्सल है।
द्वैत ध्रुवीय पारस्परिकता से निकटता से संबंधित है, ज्यामितीय परिवर्तन, जब उत्तल बहुफलक पर प्रयुक्त होता है, तो द्वैत बहुफलक को एक और उत्तल बहुफलक के रूप में अनुभव करता है।
द्वैत के प्रकार

केपलर के दुनिया के हार्मोनिक्स (1619) से छवियां
द्वैत कई प्रकार के होते हैं। प्रारंभिक बहुफलक के लिए सबसे अधिक प्रासंगिक प्रकार ध्रुवीय पारस्परिकता और सामयिक या अमूर्त द्वैत हैं।
ध्रुवीय पारस्परिकता
यूक्लिडियन अंतरिक्ष में, बहुफलक का द्वैत अधिकांशतः क्षेत्र के बारे में ध्रुवीय पारस्परिकता के संदर्भ में परिभाषित किया जाता है। यहां, प्रत्येक शीर्ष (पोल) फेस प्लेन (पोलर प्लेन या सिर्फ पोलर) से जुड़ा होता है, जिससे केंद्र से शीर्ष तक की किरण प्लेन के लंबवत हो, और केंद्र से प्रत्येक की दूरियों का गुणनफल त्रिज्या का वर्ग के समान हो ।[3]
जब गोले की त्रिज्या होती है और मूल पर केंद्रित है (जिससे समीकरण द्वारा परिभाषित किया जा सके ), फिर उत्तल बहुफलक का ध्रुवीय द्वैत की तरह परिभाषित किया गया है
जहाँ पर तथा के मानक डॉट उत्पाद को दर्शाता है
सामान्यतः जब द्वैत के निर्माण में कोई क्षेत्र निर्दिष्ट नहीं होता है, तो इकाई क्षेत्र का उपयोग किया जाता है, जिसका अर्थ है उपरोक्त परिभाषाओं में है।[4]
रैखिक समीकरण द्वारा वर्णित के प्रत्येक फलक के विमान के लिए
समरूपता के केंद्र के साथ बहुफलक के लिए, इस बिंदु पर केंद्रित गोले का उपयोग करना सामान्य है, जैसा कि द्वैत वर्दी बहुफलक डोरमैन ल्यूक निर्माण (नीचे उल्लिखित) में है। विफल होने पर, बहुफलक के लिए सीमाबद्ध क्षेत्र, खुदा हुआ क्षेत्र, या मिडस्फीयर (स्पर्शरेखा के रूप में सभी किनारों के साथ), इसका उपयोग किया जा सकता है। चूंकि, किसी भी क्षेत्र के बारे में एक बहुफलक का आदान-प्रदान करना संभव है, और द्वैत का परिणामी रूप गोले के आकार और स्थिति पर निर्भर करेगा; जिस प्रकार क्षेत्र विविध है, उसी प्रकार द्वैत रूप भी है। गोले के केंद्र का चुनाव समानता तक द्वैत को परिभाषित करने के लिए पर्याप्त है।
यदि यूक्लिडियन अंतरिक्ष में एक बहुफलक का फलक समतल, किनारे की रेखा, या शीर्ष गोले के केंद्र पर स्थित है, तो इसके द्वैत का संबंधित तत्व अनंत तक जाएगा। चूंकि यूक्लिडियन अंतरिक्ष कभी भी अनंत तक नहीं पहुंचता है, प्रक्षेपी समतुल्य, विस्तारित यूक्लिडियन अंतरिक्ष कहा जाता है, आवश्यक 'अनंत पर विमान' जोड़कर बनाया जा सकता है। कुछ सिद्धांतवादी यूक्लिडियन स्थान से चिपके रहना पसंद करते हैं और कहते हैं कि कोई द्वैत नहीं है। इस समय, वेनिंगर (1983) मॉडल (कुछ परिमित भाग के) बनाने के लिए उपयुक्त विधि से इन अनंत द्वैत का प्रतिनिधित्व करने की विधि मिली है।
यहाँ द्वैत की अवधारणा प्रक्षेपी ज्यामिति में द्वैत (प्रक्षेपी ज्यामिति) से निकटता से संबंधित है, जहाँ रेखाएँ और किनारे आपस में जुड़े होते हैं। उत्तल बहुफलक के लिए प्रोजेक्टिव पोलरिटी अधिक अच्छी तरह से काम करती है। किन्तु स्टार बहुफलक जैसे गैर-उत्तल आंकड़ों के लिए, जब हम प्रोजेक्टिव पोलरिटी के संदर्भ में पॉलीहेड्रल द्वैत के इस रूप को सख्ती से परिभाषित करना चाहते हैं, तो विभिन्न समस्याएं सामने आती हैं। [5] गैर-उत्तल बहुफलक के ज्यामितीय द्वैत के लिए निश्चित मुद्दों के कारण, ग्रुनबाउम (2007) तर्क देता है कि एक गैर-उत्तल बहुफलक की किसी भी उचित परिभाषा में द्वैत बहुफलक की धारणा सम्मिलित होनी चाहिए।
विहित द्वैत
किसी भी उत्तल बहुफलक को कैनोनिकल बहुफलक में विकृत किया जा सकता है, जिसमें एक इकाई मिडस्फीयर (या इंटरस्फीयर) हर किनारे पर स्पर्शरेखा उपस्थित होती है, और इस तरह स्पर्शरेखा के बिंदुओं की औसत स्थिति गोले का केंद्र होती है। सर्वांगसमता के लिए यह रूप अद्वितीय है।
यदि हम इस तरह के कैनोनिकल बहुफलक को इसके मिडस्फीयर के बारे में बताते हैं, तो द्वैत बहुफलक समान किनारे-स्पर्श बिंदुओं को साझा करेगा, और इस प्रकार कैनोनिकल भी होगा। यह कैनोनिकल द्वैत है, और दोनों मिलकर एक कैनोनिकल द्वैत कंपाउंड बनाते हैं।[6]
डोरमन ल्यूक निर्माण
एक समान बहुफलक के लिए, द्वैत बहुफलक के प्रत्येक फलक को मूल बहुफलक के संबंधित शीर्ष आकृति से यूनिफ़ॉर्म द्वैत बहुफलक डोर्मन ल्यूक निर्माण का उपयोग करके प्राप्त किया जा सकता है।[7]
सामयिक द्वैत
यहां तक कि जब बहुफलक की जोड़ी एक-दूसरे से पारस्परिक रूप से प्राप्त नहीं की जा सकती है, तब तक उन्हें एक-दूसरे के द्वैत कहा जा सकता है, जब तक कि एक के शीर्ष दूसरे के फलक से मिलता खाते हैं, और एक के किनारे दूसरे के किनारों से मिलता खाते हैं , घटना-संरक्षण विधि से। बहुफलक के ऐसे जोड़े अभी भी स्थलीय या अमूर्त रूप से द्वैत हैं।
उत्तल बहुफलक के कोने और किनारे एक ग्राफ सिद्धांत (एन-कंकाल | बहुफलक का 1-कंकाल) बनाते हैं, जो बहुफलक (स्थलीय क्षेत्र) की सतह पर एम्बेडेड होता है। इस ग्राफ को समतल तल पर श्लेगल आरेख बनाने के लिए प्रक्षेपित किया जा सकता है। द्वैत बहुफलक के शीर्षों और किनारों द्वारा निर्मित ग्राफ़ द्वैत ग्राफ का द्वैत ग्राफ़ है।
अधिक सामान्यतः, किसी भी बहुफलक के लिए जिसका फलक बंद सतह बनाता है, बहुफलक के कोने और किनारे इस सतह पर एम्बेडेड ग्राफ बनाते हैं, और (सार) द्वैत बहुफलक के कोने और किनारे मूल ग्राफ के द्वैत ग्राफ का निर्माण करते हैं।
एक अमूर्त पॉलीटॉप तत्वों का एक निश्चित प्रकार का आंशिक रूप से आदेशित समुच्चय (पॉसमुच्चय) है, जैसे समुच्चय के तत्वों के मध्य घटनाएँ, या कनेक्शन, बहुफलक के तत्वों (फलक, किनारों, कोने) के मध्य की घटनाओं के अनुरूप होते हैं। इस तरह के हर पॉसमुच्चय में एक द्वैत पोसमुच्चय होता है, जो सभी आदेशित संबंधों को उलट कर बनाया जाता है। यदि पोसमुच्चय को हस्स आरेख के रूप में देखा जाता है, तो हस्स आरेख को उल्टा करके द्वैत पोसमुच्चय को आसानी से देखा जा सकता है।
प्रत्येक ज्यामितीय बहुफलक इस तरह से एक सार बहुफलक से मिलता है, और इसमें अमूर्त द्वैत बहुफलक है। चूंकि, कुछ प्रकार के गैर-उत्तल ज्यामितीय बहुफलक के लिए, द्वैत बहुफलक ज्यामितीय रूप से वसूली योग्य नहीं हो सकता है।
स्व-द्वैत बहुफलक
स्थलाकृतिक रूप से, एक स्व-द्वैत बहुफलक वह है जिसके द्वैत में शीर्षों, किनारों और मुख के मध्य बिल्कुल समान संयोजकता होती है। संक्षेप में, उनके पास एक ही हस्स आरेख है।
ज्यामितीय रूप से स्व-द्वैत बहुफलक न केवल स्थैतिक रूप से स्व-द्वैत है, किन्तु निश्चित बिंदु के बारे में इसका ध्रुवीय पारस्परिक, सामान्यतः इसका केन्द्रक, एक समान आकृति है। उदाहरण के लिए, एक नियमित चतुष्फलक का द्वैत एक अन्य नियमित चतुष्फलक है, मूल के माध्यम से प्रतिबिंब बना है।
प्रत्येक बहुभुज (अर्थात्, द्वि-आयामी बहुफलक) स्थलीय रूप से स्व-द्वैत है, क्योंकि इसमें किनारों की संख्या समान है, और ये द्वैत द्वारा स्विच किए जाते हैं। किन्तु यह आवश्यक रूप से स्व-द्वैत नहीं है (उदाहरण के लिए कठोर गति तक)। प्रत्येक बहुभुज में एक नियमित बहुभुज होता है जो ज्यामितीय रूप से अपने चौराहों के बारे में आत्म-द्वैत होता है: सभी कोण सर्वांगसम होते हैं, जैसा कि सभी किनारे होते हैं, इसलिए द्वैत के अनुसार ये सर्वांगसमताएँ अदला-बदली करती हैं।
इसी तरह, प्रत्येक टोपोलॉजिकल रूप से स्व-द्वैत उत्तल बहुफलक को समतुल्य ज्यामितीय रूप से स्व-द्वैत बहुफलक द्वारा अनुभव किया जा सकता है, इसके कैनोनिकल बहुफलक, मिडस्फीयर के केंद्र के बारे में पारस्परिक है।
सामान्यतः कई ज्यामितीय स्व-द्वैत बहुफलक हैं। सबसे सरल अनंत वर्ग 'एन' पक्षों के विहित पिरामिड (ज्यामिति) हैं। एक अन्य अनंत वर्ग, लम्बी पिरामिड, में बहुफलक होते हैं जिन्हें सामान्यतः प्रिज्म (ज्यामिति) के शीर्ष पर बैठे पिरामिड के रूप में वर्णित किया जा सकता है (समान संख्या में पक्षों के साथ)। प्रिज्म के नीचे एक छिन्नक (पिरामिड जिसका शीर्ष कटा हुआ है) जोड़ने से एक और अनंत वर्ग उत्पन्न होता है, और इसी तरह आगे भी उत्पन्न होता है।
कई अन्य उत्तल, स्व-द्वैत बहुफलक हैं। उदाहरण के लिए, 7 शीर्षों के साथ 6 भिन्न हैं, और 8 शीर्षों के साथ 16 हैं।[8]
1900 में ब्रुकनर द्वारा हेक्सागोनल मुख के साथ एक स्व-द्वैत गैर-उत्तल आईकोसाहेड्रॉन की पहचान की गई थी। [9][10][11] गैर-उत्तल बहुफलक और उनके द्वैत की कुछ परिभाषाओं के अनुसार अन्य गैर-उत्तल स्व-द्वैत बहुफलक पाए गए हैं।
 3 |
 4 |
 5 |
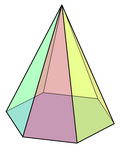 6 |
 3 |
 4 |
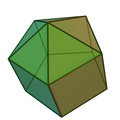 5 |
 3 |
 4 |
 5 |
 6 |
 7 |
द्वैत पॉलीटॉप और टेसलेशन
द्वैत को एन-डायमेंशनल स्पेस और 'द्वैत पॉलीटोप्स' के लिए सामान्यीकृत किया जा सकता है; द्विविम में इन्हें द्विबहुभुज कहते हैं।
एक पॉलीटॉप के शीर्ष दूसरे के (n - 1)-विमीय तत्वों, या पहलुओं के अनुरूप होते हैं, और j बिंदु जो a (j - 1)-आयामी तत्व को परिभाषित करते हैं, वे j हाइपरप्लेन के अनुरूप होंगे जो एक ( एन - जे) - आयामी तत्व है। एक एन-डायमेंशनल टेसलेशन या हनीकॉम्ब (ज्यामिति) के द्वैत को इसी तरह परिभाषित किया जा सकता है।
सामान्यतः, पॉलीटोप के द्वैत के पहलू पॉलीटॉप के शीर्ष आंकड़ों के टोपोलॉजिकल द्वैत होंगे। नियमित पॉलीटॉप और वर्दी पॉलीटॉप पॉलीटोप्स के ध्रुवीय व्युत्क्रम के लिए, द्वैत पहलू मूल के शीर्ष आकृति के ध्रुवीय व्युत्क्रम होंगे। उदाहरण के लिए, चार आयामों में, 600-सेल का शीर्ष आंकड़ा नियमित आईकोसाहेड्रॉन है; 600-कोशिका का द्वैत 120-कोशिका है, जिसके पहलू द्वादशफ़लक हैं, जो कि विंशतिफलक के द्वैत हैं।
स्व-द्वैत पॉलीटोप्स और टेसलेशन्स


स्व-द्वैत पॉलीटॉप्स का प्राथमिक वर्ग मुरजबंध संबंधी फलक प्रतीकों के साथ नियमित पॉलीटोप्स हैं। सभी नियमित बहुभुज, {ए} स्व-द्वैत हैं, फॉर्म के बहुफलक {ए}, फॉर्म के 4-पॉलीटॉप {ए, बी, ए}, फॉर्म के 5-पॉलीटॉप {ए, बी, बी, ए }, आदि।
स्व-द्वैत नियमित पॉलीटॉप हैं:
- सभी नियमित बहुभुज, {ए}।
- नियमित चतुष्फलक: {3,3}
- सामान्यतः, सभी नियमित सिंप्लेक्स, {3,3,...,3}
- 4 आयामों में नियमित 24-कोशिका, {3,4,3}।
- महान 120-सेल {5,5/2,5} और भव्य तारकीय 120-सेल {5/2,5,5/2}
स्व-द्वैत (अनंत) नियमित यूक्लिडियन मधुकोश (ज्यामिति) हैं:
- एपिरोगोन: {∞}
- स्क्वायर टाइलिंग: {4,4}
- क्यूबिक मधुकोश: {4,3,4}
- सामान्यतः, सभी नियमित एन-डायमेंशनल यूक्लिडियन हाइपरक्यूबिक मधुकोश: {4,3,...,3,4}।
स्व-द्वैत (अनंत) नियमित कॉक्समुच्चयर आरेख हाइपरबोलिक कॉक्समुच्चयर समूह मधुकोश हैं:
- कॉम्पैक्ट हाइपरबोलिक टाइलिंग: ऑर्डर-5 पंचकोणीय टाइलिंग|{5,5}, ऑर्डर-6 हेक्सागोनल टाइलिंग|{6,6}, ... {पी,पी}।
- पैराकॉम्पैक्ट हाइपरबोलिक टाइलिंग: अनंत-क्रम एपिरोगोनल टाइलिंग|{∞,∞}
- कॉम्पैक्ट हाइपरबोलिक मधुकोश: इकोसाहेड्रल हनीकॉम्ब|{3,5,3}, ऑर्डर-5 डोडेकाहेड्रल हनीकॉम्ब|{5,3,5}, और ऑर्डर-5 120-सेल हनीकॉम्ब|{5,3,3,5}
- पैराकॉम्पैक्ट हाइपरबोलिक हनीकॉम्ब: त्रिकोणीय टाइलिंग हनीकॉम्ब|{3,6,3}, ऑर्डर-6 हेक्सागोनल टाइलिंग हनीकॉम्ब|{6,3,6}, ऑर्डर-4 स्क्वायर टाइलिंग हनीकॉम्ब|{4,4,4}, और {3 ,3,4,3,3}
यह भी देखें
- कॉनवे बहुफलक नोटेशन
- द्वैत बहुभुज
- स्व-द्वैत ग्राफ
- स्व-द्वैत बहुभुज
संदर्भ
टिप्पणियाँ
- ↑ Wenninger (1983), "Basic notions about stellation and duality", p. 1.
- ↑ Grünbaum (2003)
- ↑ Cundy & Rollett (1961), 3.2 Duality, pp. 78–79; Wenninger (1983), Pages 3-5. (Note, Wenninger's discussion includes nonconvex polyhedra.)
- ↑ Barvinok (2002), Page 143.
- ↑ See for example Grünbaum & Shephard (2013), and Gailiunas & Sharp (2005). Wenninger (1983) also discusses some issues on the way to deriving his infinite duals.
- ↑ Grünbaum (2007), Theorem 3.1, p. 449.
- ↑ Cundy & Rollett (1961), p. 117; Wenninger (1983), p. 30.
- ↑ 3D Java models at Symmetries of Canonical Self-Dual Polyhedra, based on paper by Gunnar Brinkmann, Brendan D. McKay, Fast generation of planar graphs PDF [1]
- ↑ Anthony M. Cutler and Egon Schulte; "Regular Polyhedra of Index Two", I; Beiträge zur Algebra und Geometrie / Contributions to Algebra and Geometry April 2011, Volume 52, Issue 1, pp 133–161.
- ↑ N. J. Bridge; "Faceting the Dodecahedron", Acta Crystallographica, Vol. A 30, Part 4 July 1974, Fig. 3c and accompanying text.
- ↑ Brückner, M.; Vielecke und Vielflache: Theorie und Geschichte, Teubner, Leipzig, 1900.
ग्रन्थसूची
- Cundy, H. Martyn; Rollett, A. P. (1961), Mathematical Models (2nd ed.), Oxford: Clarendon Press, MR 0124167.
- Gailiunas, P.; Sharp, J. (2005), "Duality of polyhedra", International Journal of Mathematical Education in Science and Technology, 36 (6): 617–642, doi:10.1080/00207390500064049, S2CID 120818796.
- Grünbaum, Branko (2003), "Are your polyhedra the same as my polyhedra?", in Aronov, Boris; Basu, Saugata; Pach, János; Sharir, Micha (eds.), Discrete and Computational Geometry: The Goodman–Pollack Festschrift, Algorithms and Combinatorics, vol. 25, Berlin: Springer, pp. 461–488, CiteSeerX 10.1.1.102.755, doi:10.1007/978-3-642-55566-4_21, ISBN 978-3-642-62442-1, MR 2038487.
- Grünbaum, Branko (2007), "Graphs of polyhedra; polyhedra as graphs", Discrete Mathematics, 307 (3–5): 445–463, doi:10.1016/j.disc.2005.09.037, hdl:1773/2276, MR 2287486.
- Grünbaum, Branko; Shephard, G. C. (2013), "Duality of polyhedra", in Senechal, Marjorie (ed.), Shaping Space: Exploring polyhedra in nature, art, and the geometrical imagination, New York: Springer, pp. 211–216, doi:10.1007/978-0-387-92714-5_15, ISBN 978-0-387-92713-8, MR 3077226.
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 0-521-54325-8, MR 0730208.
- Barvinok, Alexander (2002), A course in convexity, Providence: American Mathematical Soc., ISBN 0821829688.
