पाई चार्ट: Difference between revisions
m (6 revisions imported from alpha:पाई_चार्ट) |
No edit summary |
||
| Line 127: | Line 127: | ||
* [[Leland Wilkinson|Wilkinson, Leland]]. ''The Grammar of Graphics'', 2nd edition. Springer, 2005. {{ISBN|0-387-24544-8}}. | * [[Leland Wilkinson|Wilkinson, Leland]]. ''The Grammar of Graphics'', 2nd edition. Springer, 2005. {{ISBN|0-387-24544-8}}. | ||
[[Category:All articles with unsourced statements]] | |||
[[Category: | [[Category:Articles with hatnote templates targeting a nonexistent page]] | ||
[[Category:Articles with unsourced statements from October 2017]] | |||
[[Category:CS1 English-language sources (en)]] | |||
[[Category: | |||
[[Category:Created On 28/02/2023]] | [[Category:Created On 28/02/2023]] | ||
[[Category:Vigyan Ready]] | [[Category:Lua-based templates]] | ||
[[Category:Machine Translated Page]] | |||
[[Category:Pages with script errors]] | |||
[[Category:Short description with empty Wikidata description]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:Templates that add a tracking category]] | |||
[[Category:Templates that generate short descriptions]] | |||
[[Category:Templates using TemplateData]] | |||
[[Category:सांख्यिकीय चार्ट और आरेख]] | |||
Latest revision as of 07:35, 19 March 2023

पाई चार्ट (या वृत्त चार्ट) एक गोलाकार सांख्यिकीय ग्राफिक है, जो संख्यात्मक अनुपात को दर्शाने के लिए टुकड़ों में विभाजित होता है। एक पाई चार्ट में, प्रत्येक टुकड़े की चाप की लंबाई (और इसके परिणामस्वरूप इसका केंद्रीय कोण और क्षेत्र) उस मात्रा के समानुपाती होता है जिसका वह प्रतिनिधित्व करता है। जबकि इसका नाम एक पाई के समान होने के लिए रखा गया है जिसे काटा गया है, इसे प्रस्तुत करने के तरीके में भिन्नताएँ हैं। सबसे पहले ज्ञात पाई चार्ट को प्रायः 1801 के विलियम प्लेफेयर के सांख्यिकीय ब्रेविएरी को श्रेय दिया जाता है।[1][2]
व्यापार जगत और जनसंचार माध्यमों में पाई चार्ट का व्यापक रूप से उपयोग किया जाता है।[3] हालांकि, उनकी आलोचना की गई है,[4] और कई विशेषज्ञ उनसे बचने की सलाह देते हैं,[5][6][7][8] क्योंकि शोध से पता चला है कि दिए गए पाई चार्ट के विभिन्न वर्गों की तुलना करना या विभिन्न पाई चार्ट में डेटा की तुलना करना मुश्किल है। ज्यादातर स्थितियों में पाई चार्ट को अन्य प्लॉट जैसे बार चार्ट, बॉक्स प्लॉट, डॉट प्लॉट आदि से बदला जा सकता है।
इतिहास
सबसे पहले ज्ञात पाई चार्ट को प्रायः 1801 के विलियम प्लेफेयर के सांख्यिकीय ब्रेविअरी को श्रेय दिया जाता है, जिसमें दो ऐसे ग्राफ का उपयोग किया जाता है।[1][2][9] प्लेफेयर ने एक उदाहरण प्रस्तुत किया, जिसमें पाई चार्ट की श्रृंखला सम्मिलित थी। इनमें से एक चार्ट में 1789 से पहले एशिया, यूरोप और अफ्रीका में स्थित तुर्की साम्राज्य के अनुपात को दर्शाया गया था। इस आविष्कार का पहले व्यापक रूप से उपयोग नहीं किया गया था।[1]
प्लेफेयर ने सोचा कि अतिरिक्त जानकारी जोड़ने के लिए पाई चार्ट को त्रि आयाम की आवश्यकता थी।[10]
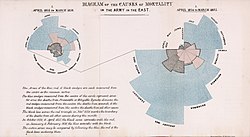
फ्लोरेंस नाइटेंगल ने भले ही पाई चार्ट का आविष्कार नहीं किया हो, लेकिन उन्होंने इसे अधिक पठनीय बनाने के लिए इसे अनुकूलित किया, जिसने आज भी इसके व्यापक उपयोग को बढ़ावा दिया। वास्तव में, नाइटेंगल ने पाई चार्ट को फिर से कॉन्फ़िगर किया, जिससे वेजेज की लंबाई उनकी चौड़ाई के स्थान पर चर हो गई। ग्राफ, तब, एक मुर्गे की कंघी जैसा दिखता था।[11] बाद में यह मान लिया गया था कि प्लेफेयर के निर्माण की अस्पष्टता और व्यावहारिकता की कमी के कारण इसे बनाया गया था।[12] नाइटेंगल का ध्रुवीय क्षेत्र आरेख,[13]: 107 या कभी-कभी नाइटेंगल गुलाब आरेख, एक आधुनिक वृत्ताकार हिस्टोग्राम के समतुल्य, सैन्य क्षेत्र के अस्पताल में रोगी मृत्यु दर के मौसमी स्रोतों को स्पष्ट करने के लिए, ब्रिटिश सेना के स्वास्थ्य, दक्षता और अस्पताल प्रशासन को प्रभावित करने वाले मामलों पर नोट्स में प्रकाशित किया गया था और 1858 में महारानी विक्टोरिया को भेजा गया था। इतिहासकार ह्यूग स्मॉल के अनुसार, "हो सकता है कि वह परिवर्तन की आवश्यकता के बारे में लोगों को समझाने के लिए [पाई चार्ट] का उपयोग करने वाली पहली महिला रही हों।"[11]
1858 में फ्रांसीसी इंजीनियर चार्ल्स जोसेफ मिनार्ड ने भी पाई चार्ट का उपयोग किया था। 1858 के उनके एक मानचित्र में पेरिस में उपभोग के लिए पूरे फ्रांस से भेजे गए मवेशियों का प्रतिनिधित्व करने के लिए पाई चार्ट का उपयोग किया गया था।
फ्लोरेंस नाइटेंगल, 1858 द्वारा ध्रुवीय चार्ट
भिन्नरूप और समान चार्ट
3डी पाई चार्ट और परिप्रेक्ष्य पाई केक
एक 3डी पाई चार्ट, या परिप्रेक्ष्य पाई चार्ट का उपयोग चार्ट को 3डी रूप देने के लिए किया जाता है। प्रायः सौंदर्य संबंधी कारणों के लिए उपयोग किया जाता है, त्रि आयाम डेटा पढ़ने में सुधार नहीं करता है, इसके विपरीत, त्रि आयाम से जुड़े परिप्रेक्ष्य के विकृत प्रभाव के कारण इन भूखंडों की व्याख्या करना कठिन है। रुचि के डेटा को प्रदर्शित करने के लिए उपयोग नहीं किए जाने वाले अनावश्यक आयामों का उपयोग चार्ट के लिए सामान्य रूप से हतोत्साहित किया जाता है, न केवल पाई चार्ट के लिए।[7][14]
डोनट चार्ट
डोनट चार्ट (वर्तनी डोनट भी) पाई चार्ट का एक प्रकार है, जिसमें रिक्त केंद्र होता है, जो संपूर्ण डेटा के बारे में अतिरिक्त जानकारी को सम्मिलित करने की अनुमति देता है।[15][16] डोनट चार्ट पाई चार्ट के समान होते हैं जिसमें उनका उद्देश्य अनुपात को दर्शाना होता है।[citation needed] इस प्रकार का वृत्ताकार ग्राफ एक साथ कई आँकड़ों का समर्थन कर सकता है और यह मानक पाई चार्ट को बेहतर डेटा तीव्रता अनुपात प्रदान करता है।[16] इसमें केंद्र में जानकारी होना जरूरी नहीं है।
खंडित पाई चार्ट
चार्ट जिसमें एक या एक से अधिक क्षेत्र शेष डिस्क से अलग होते हैं, खंडित पाई चार्ट के रूप में जाना जाता है। इस प्रभाव का उपयोग या तो किसी क्षेत्र को हाइलाइट करने के लिए किया जाता है, या चार्ट के छोटे खंडों को छोटे अनुपात के साथ हाइलाइट करने के लिए किया जाता है।
ध्रुवीय क्षेत्र आरेख
ध्रुवीय क्षेत्र आरेख एक सामान्य पाई चार्ट के समान है, बजाय इसके कि क्षेत्रों में समान कोण होते हैं और प्रत्येक क्षेत्र वृत्त के केंद्र से कितनी दूर तक फैला होता है, इसके स्थान पर भिन्न होते है। ध्रुवीय क्षेत्र आरेख का उपयोग चक्रीय परिघटनाओं (जैसे, महीने के अनुसार मौतों की संख्या) को प्लॉट करने के लिए किया जाता है। उदाहरण के लिए, यदि एक वर्ष के लिए प्रत्येक महीने में होने वाली मौतों की गणना की जानी है, तो 12 क्षेत्र (प्रति माह एक) होंगे, जिनमें प्रत्येक 30 डिग्री के समान कोण होंगे। प्रत्येक क्षेत्र की त्रिज्या महीने के लिए मृत्यु दर के वर्गमूल के समानुपाती होगा, इसलिए किसी क्षेत्र का क्षेत्रफल एक महीने में मौतों की दर को दर्शाता है। यदि प्रत्येक महीने में मृत्यु दर को मृत्यु के कारण उप-विभाजित किया जाता है, तो आरेख पर कई तुलना करना संभव है, जैसा कि फ्लोरेंस नाइटेंगल द्वारा प्रसिद्ध रूप से विकसित ध्रुवीय क्षेत्र आरेख में देखा गया है।
ध्रुवीय क्षेत्र आरेखों का पहला ज्ञात उपयोग आंद्रे-माइकल गुएरी द्वारा किया गया था, जिसे उन्होंने 1829 के एक पेपर में कर्बस सर्कुलेयर्स (परिपत्र वक्र) कहा था, जो वर्ष भर हवा की दिशा में मौसमी और दैनिक भिन्नता और दिन के घंटे के अनुसार जन्म और मृत्यु दर्शाता है।[17] लियोन लल्ने ने बाद में 1843 में दिशासूचक बिंदुओं के आसपास वायु की दिशाओं की आवृत्ति दिखाने के लिए ध्रुवीय आरेख का उपयोग किया। पवन गुलाब अभी भी मौसम विज्ञानियों द्वारा उपयोग किया जाता है। नाइटेंगल ने 1858 में अपना गुलाब का आरेख प्रकाशित किया। यद्यपि "कॉक्सकॉम्ब" नाम इस प्रकार के आरेख के साथ जुड़ा हुआ है, नाइटेंगल ने मूल रूप से इस शब्द का उपयोग उस प्रकाशन को संदर्भित करने के लिए किया था जिसमें यह चित्र पहली बार इस विशिष्ट प्रकार के आरेख के स्थान पर चार्ट और तालिकाओं की एक ध्यान आकर्षित करने वाली पुस्तक के रूप में सामने आया था।[18]
रिंग चार्ट, सनबर्स्ट चार्ट, और बहुस्तरीय पाई चार्ट
रिंग चार्ट, जिसे सनबर्स्ट चार्ट या बहुस्तरीय पाई चार्ट के रूप में भी जाना जाता है, का उपयोग संकेंद्रित वृत्तों द्वारा दर्शाए गए पदानुक्रमित डेटा को देखने के लिए किया जाता है।[19] केंद्र में वृत्त रूट नोड का प्रतिनिधित्व करता है, जिसमें पदानुक्रम केंद्र से बाहर की ओर बढ़ता है। आंतरिक वृत्त का एक खंड बाहरी वृत्त के उन खंडों के लिए एक पदानुक्रमित संबंध रखता है जो मूल खंड के कोणीय विस्तार के भीतर स्थित हैं।[20][21]
स्पाई चार्ट
ध्रुवीय क्षेत्र चार्ट का एक प्रकार स्पाई चार्ट है, जिसे ड्रोर फेइटल्सन द्वारा डिजाइन किया गया है।[22] संबंधित डेटा के दो सेटों की तुलना करने की अनुमति देने के लिए डिजाइन संशोधित ध्रुवीय क्षेत्र चार्ट के साथ एक सामान्य पाई चार्ट को अध्यारोपित करता है। आधार पाई चार्ट विभिन्न टुकड़े आकारों के साथ सामान्य तरीके से पहले डेटा सेट का प्रतिनिधित्व करता है। दूसरे सेट को आधार के समान कोणों का उपयोग करके और डेटा को उपयुक्त करने के लिए त्रिज्या को समायोजित करके अध्यारोपित ध्रुवीय क्षेत्र चार्ट द्वारा दर्शाया गया है। उदाहरण के लिए, आधार पाई चार्ट जनसंख्या में आयु और लिंग समूहों के वितरण को दिखा सकता है, और सड़क दुर्घटनाओं के बीच उनके प्रतिनिधित्व को आच्छादन कर सकता है।
वर्ग चार्ट / वफ़ल चार्ट
वर्ग चार्ट, जिसे वफ़ल चार्ट भी कहा जाता है, पाई चार्ट का एक रूप है जो प्रतिशत का प्रतिनिधित्व करने के लिए वृत्त के स्थान पर वर्गों का उपयोग करता है। बेसिक वृत्तीय पाई चार्ट के समान, वर्ग पाई चार्ट प्रत्येक प्रतिशत को कुल 100% में से लेते हैं। वे प्रायः 10 गुणा 10 ग्रिड होते हैं, जहां प्रत्येक कोशिका 1% का प्रतिनिधित्व करती है। नाम के बावजूद, वर्गों के स्थान पर वृत्त, चित्रलेख (जैसे कि लोगों के), और अन्य आकृतियों का उपयोग किया जा सकता है। वर्गाकार चार्ट का एक प्रमुख लाभ यह है कि छोटे प्रतिशत, जिन्हें पारंपरिक पाई चार्ट पर देखना कठिन होता है, को आसानी से दर्शाया जा सकता है।[23]
उदाहरण
निम्नलिखित उदाहरण चार्ट 2004 में यूरोपीय संसद के चुनाव के प्रारंभिक परिणामों पर आधारित है। तालिका प्रत्येक पार्टी समूह को आवंटित सीटों की संख्या को सूचीबद्ध करती है, साथ ही उनमें से प्रत्येक के कुल योग का व्युत्पन्न प्रतिशत भी। अंतिम स्तंभ में मान, प्रत्येक त्रिज्यखंड का व्युत्पन्न केंद्रीय कोण, प्रतिशत को 360° से गुणा करके पाया जाता है।
| समूह | सीटें | प्रतिशत (%) | केन्द्रीय कोण (°) |
|---|---|---|---|
| ईयूएल (EUL) | 39 | 5.3 | 19.2 |
| पीईएस (PES) | 200 | 27.3 | 98.4 |
| ईएफए (EFA) | 42 | 5.7 | 20.7 |
| ईडीडी (EDD) | 15 | 2.0 | 7.4 |
| ईएलडीआर (ELDR) | 67 | 9.2 | 33.0 |
| ईपीपी (EPP) | 276 | 37.7 | 135.7 |
| यूईएन (UEN) | 27 | 3.7 | 13.3 |
| अन्य | 66 | 9.0 | 32.5 |
| कुल | 732 | 99.9* | 360.2* |
*गोलाई के कारण, इन योगों का जोड़ 100 और 360 नहीं होता है।
प्रत्येक केंद्रीय कोण का आकार संबंधित मात्रा के आकार के समानुपाती होता है, यहाँ सीटों की संख्या होती है। चूँकि केंद्रीय कोणों का योग 360° होना चाहिए, एक मात्रा के लिए केंद्रीय कोण जो कुल का एक भिन्न Q है, 360Q डिग्री है। उदाहरण में, सबसे बड़े समूह (यूरोपियन पीपल्स पार्टी (EPP)) के लिए केंद्रीय कोण 135.7° है क्योंकि 0.377 गुना 360, एक दशमलव स्थान पर पूर्णांकित, 135.7 के बराबर है।
उपयोग और प्रभावशीलता
पाई चार्ट द्वारा प्रदर्शित एक दोष यह है कि वे दृश्य एन्कोडिंग ("स्लाइस") को उनके द्वारा प्रस्तुत डेटा (प्रायः प्रतिशत) से अलग किए बिना कुछ मानों से अधिक नहीं दिखा सकते हैं। जब टुकड़े बहुत छोटे हो जाते हैं, तो पाई चार्ट को रंग, बनावट या तीरों पर निर्भर रहना पड़ता है ताकि पाठक उन्हें समझ सकें। यह उन्हें बड़ी मात्रा में डेटा के साथ प्रयोग करने के लिए अनुपयुक्त बनाता है। पाई चार्ट अधिक लचीले बार चार्ट की तुलना में पृष्ठ पर अधिक स्थान घेरते हैं, जिसमें अलग-अलग आलेख होने की आवश्यकता नहीं होती है, और एक ही समय में औसत या लक्ष्य जैसे अन्य मान प्रदर्शित कर सकते हैं।[7]
सांख्यिकीविद् प्रायः पाई चार्ट को जानकारी प्रदर्शित करने की एक खराब विधि के रूप में देखते हैं, और वे वैज्ञानिक साहित्य में असामान्य हैं। एक कारण यह है कि किसी चार्ट में वस्तुओं के आकार के बीच तुलना करना अधिक कठिन होता है जब लंबाई के स्थान पर क्षेत्र का उपयोग किया जाता है और जब विभिन्न वस्तुओं को विभिन्न आकृतियों के रूप में दिखाया जाता है।[24]
इसके अलावा, एटी एंड टी (AT&T) बेल लेबोरेटरीज में किए गए शोध में यह दिखाया गया था कि लंबाई की तुलना में कोण द्वारा तुलना कम सटीक थी। अधिकांश विषयों को पाई चार्ट में टुकड़े को आकार के अनुसार व्यवस्थित करने में कठिनाई होती है; जब समतुल्य बार चार्ट का उपयोग किया जाता है तो तुलना करना बहुत आसान हो जाता है।[25] इसी तरह, बार चार्ट का उपयोग करके डेटा सेट के बीच तुलना करना आसान होता है। हालाँकि, यदि लक्ष्य किसी एकल चार्ट में कुल (संपूर्ण पाई) के साथ दी गई श्रेणी (पाई का एक टुकड़ा) की तुलना करना है और गुणक 25 या 50 प्रतिशत के समीप है, तो पाई चार्ट प्रायः बार ग्राफ से अधिक प्रभावी हो सकता है।[26][27]
कई अनुभागों वाले पाई चार्ट में, कई मानों को समान या समान रंगों से प्रदर्शित किया जा सकता है, जिससे व्याख्या करना कठिन हो जाता है।
यूरोपीय प्रत्यक्षीकरण सम्मेलन में प्रस्तुत कई अध्ययनों ने कई पाई चार्ट स्वरूपों की सापेक्ष सटीकता का विश्लेषण किया,[28][29][23] इस निष्कर्ष पर पहुंचे कि पाई चार्ट और डोनट चार्ट उन्हें पढ़ते समय समान त्रुटि स्तर उत्पन्न करते हैं, और वर्ग पाई चार्ट सबसे सटीक अध्ययन प्रदान करते हैं।[30]
यह भी देखें
संदर्भ
- ↑ 1.0 1.1 1.2 Spence (2005)
- ↑ 2.0 2.1 Tufte, p. 44
- ↑ Cleveland, p. 262
- ↑ Wilkinson, p. 23.
- ↑ Tufte, p. 178.
- ↑ van Belle, p. 160–162.
- ↑ 7.0 7.1 7.2 Stephen Few. "Save the Pies for Dessert", August 2007, Retrieved 2010-02-02
- ↑ Steve Fenton "Pie Charts Are Bad"
- ↑ "Milestones in the History of Thematic Cartography, Statistical Graphics, and Data Visualization". www.datavis.ca.
- ↑ Palsky, p. 144–145
- ↑ 11.0 11.1 Greenbaum, Hilary; Rubinstein, Dana (20 April 2012). "Who Made That Pie Chart?". The New York Times.
- ↑ Dave article on this information on QI
- ↑ Cohen, I. Bernard (March 1984). "फ्लोरेंस नाइटेंगल". Scientific American. 250 (3): 128–137. Bibcode:1984SciAm.250c.128C. doi:10.1038/scientificamerican0384-128. PMID 6367033. (alternative pagination depending on country of sale: 98–107, bibliography on p. 114) online article – see documents link at left
- ↑ Good and Hardin, chapter 8.
- ↑ Harris, Robert L. (1999). Information graphics : a comprehensive illustrated reference ([Nachdr.] ed.). Oxford: Oxford University Press. p. 143. ISBN 9780195135329.
- ↑ 16.0 16.1 iBooks पर Juergen Kai-Uwe Brock द्वारा डेटा डिज़ाइन. Retrieved 2017-06-10.
{{cite book}}:|website=ignored (help) - ↑ Friendly, p. 509
- ↑ "फ्लोरेंस नाइटिंगेल के सांख्यिकीय आरेख". Retrieved 2010-11-22.
- ↑ "बहु-स्तरीय पाई चार्ट". www.neoformix.com.
- ↑ Webber Richard, Herbert Ric, Jiangbc Wel. "Space-filling Techniques in Visualizing Output from Computer Based Economic Models"
- ↑ "पाई चार्ट निर्माता". piechartmaker.co.
- ↑ "Feitelson, Dror (2003) Comparing Partitions With Spie Charts" (PDF). 2003. Retrieved 2010-08-31.
- ↑ 23.0 23.1 Kosara, Robert; Skau, Drew (2016). "पाई चार्ट विविधताओं में निर्णय त्रुटि". EuroVis.
- ↑ Krygier, John (28 August 2007). "मानचित्र प्रतीकों का अवधारणात्मक स्केलिंग". makingmaps.net. Retrieved 3 May 2015.
- ↑ Cleveland, p. 86–87
- ↑ Simkin, D., & Hastie, R. (1987). An Information-Processing Analysis of Graph Perception. Journal of the American Statistical Association, 82(398), 454. doi:10.2307/2289447. Kosara, Robert (13 April 2011). "In Defense of Pie Charts". Retrieved April 13, 2011.
- ↑ Spence, Ian; Lewandowsky, Stephan (1 January 1991). "अनुपात और प्रतिशत प्रदर्शित करना". Applied Cognitive Psychology. 5 (1): 61–77. doi:10.1002/acp.2350050106.
- ↑ "पाई चार्ट अध्ययन परिणामों का एक इलस्ट्रेटेड टूर". eagereyes (in English). 2016-06-28. Retrieved 2016-11-28.
- ↑ Skau, Drew; Kosara, Robert (2016). "Arcs, Angles, or Areas: Individual Data Encodings in Pie and Donut Charts". EuroVis.
- ↑ "A Reanalysis of A Study About (Square) Pie Charts from 2009". eagereyes (in English). 2016-07-11. Retrieved 2016-11-28.
अग्रिम पठन
- Cleveland, William S. (1985). The Elements of Graphing Data. Pacific Grove, CA: Wadsworth & Advanced Book Program. ISBN 0-534-03730-5.
- Friendly, Michael. "The Golden Age of Statistical Graphics," Statistical Science, Volume 23, Number 4 (2008), 502-535
- Good, Phillip I. and Hardin, James W. Common Errors in Statistics (and How to Avoid Them). Wiley. 2003. ISBN 0-471-46068-0.
- Guerry, A.-M. (1829). Tableau des variations météorologique comparées aux phénomènes physiologiques, d'aprés les observations faites à l'obervatoire royal, et les recherches statistique les plus récentes. Annales d'Hygiène Publique et de Médecine Légale, 1 :228-.
- Harris, Robert L. (1999). Information Graphics: A comprehensive Illustrated Reference. Oxford University Press. ISBN 0-19-513532-6.
- Lima, Manuel. "Why humans love pie charts: an historical and evolutionary perspective," Noteworthy, July 23, 2018
- Palsky Gilles. Des chiffres et des cartes: la cartographie quantitative au XIXè siècle. Paris: Comité des travaux historiques et scientifiques, 1996. ISBN 2-7355-0336-4.
- Playfair, William, Commercial and Political Atlas and Statistical Breviary, Cambridge University Press (2005) ISBN 0-521-85554-3.
- Spence, Ian. No Humble Pie: The Origins and Usage of a statistical Chart. Journal of Educational and Behavioral Statistics. Winter 2005, 30 (4), 353–368.
- Tufte, Edward. The Visual Display of Quantitative Information. Graphics Press, 2001. ISBN 0-9613921-4-2.
- Van Belle, Gerald. Statistical Rules of Thumb. Wiley, 2002. ISBN 0-471-40227-3.
- Wilkinson, Leland. The Grammar of Graphics, 2nd edition. Springer, 2005. ISBN 0-387-24544-8.