पेट्री नेट: Difference between revisions
No edit summary |
No edit summary |
||
| (8 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|One of several mathematical modeling systems for the description of distributed systems}} | {{Short description|One of several mathematical modeling systems for the description of distributed systems}} | ||
पेट्री नेट, जिसे एक स्थान/संक्रमण (पीटी) नेट के रूप में भी जाना जाता है, वितरित प्रणाली के विवरण के लिए कई [[गणितीय]] [[मॉडलिंग भाषा|मॉडलिंग भाषाओं]] में से एक होता है। यह [[असतत घटना गतिशील प्रणाली]] का एक वर्ग है। पेट्री नेट एक निर्देशित द्विपक्षीय ग्राफ है जिसमें दो प्रकार के तत्व, स्थान और संक्रमण होते है। स्थान तत्वों को सफेद घेरे के रूप में दर्शाया गया है और संक्रमण तत्वों को आयतों के रूप में दर्शाया गया है। किसी स्थान में कितने भी टोकन हो सकते है, जिन्हें काले घेरों के रूप में दर्शाया गया है। यदि इनपुट के रूप में इससे जुड़े सभी स्थानों में कम से कम एक टोकन हो तो एक संक्रमण सक्षम हो जाता है। कुछ स्रोत<ref>{{cite journal | first1 = Carl Adam | last1 = Petri | first2 = Wolfgang | last2 = Reisig | date = 2008 | title = पेट्री नेट| journal = [[Scholarpedia]] | volume = 3 | issue = 4 | page = 6477 | doi=10.4249/scholarpedia.6477| bibcode = 2008SchpJ...3.6477P | doi-access = free }}</ref> कहते है कि रासायनिक प्रक्रियाओं का वर्णन करने के उद्देश्य से अगस्त 1939 में [[कार्ल एडम पेट्री]] द्वारा 13 साल की उम्र में पेट्री नेट का आविष्कार किया गया था। | |||
यूएमएल गतिविधि आरेख, [[बिजनेस प्रोसेस मॉडल और नोटेशन]], और घटना-संचालित प्रक्रिया श्रृंखला जैसे उद्योग मानकों की तरह, पेट्री नेट चरणवार प्रक्रियाओं के लिए ग्राफिकल नोटेशन प्रदान करते | यूएमएल गतिविधि आरेख, [[बिजनेस प्रोसेस मॉडल और नोटेशन]], और घटना-संचालित प्रक्रिया श्रृंखला जैसे उद्योग मानकों की तरह, पेट्री नेट चरणवार प्रक्रियाओं के लिए ग्राफिकल नोटेशन प्रदान करते है जिसमें पसंद, पुनरावृत्ति और [[समवर्ती कंप्यूटिंग|समवर्ती]] निष्पादन सम्मलित होते है। इन मानकों के विपरीत, पेट्री नेट के पास प्रक्रिया विश्लेषण के लिए एक सुविकसित गणितीय सिद्धांत के साथ उनके निष्पादन शब्दार्थ की एक त्रुटिहीन गणितीय परिभाषा है। | ||
[[Image:Animated Petri net commons.gif|thumb|(ए) पेट्री नेट प्रक्षेपवक्र उदाहरण]] | [[Image:Animated Petri net commons.gif|thumb|(ए) पेट्री नेट प्रक्षेपवक्र उदाहरण]] | ||
== ऐतिहासिक पृष्ठभूमि == | == ऐतिहासिक पृष्ठभूमि == | ||
जर्मन कंप्यूटर वैज्ञानिक कार्ल एडम पेट्री, जिनके | जर्मन कंप्यूटर वैज्ञानिक कार्ल एडम पेट्री, जिनके नाम पर इस तरह की संरचनाओं का नाम दिया गया है, उन्होने अपने 1962 के निबंध कॉम्यूनिकेशन मिट ऑटोमेटन में पेट्री नेट का बड़े पैमाने पर विश्लेषण किया था। | ||
== पेट्री नेट मूल बातें == | == पेट्री नेट मूल बातें == | ||
पेट्री नेट में स्थान, संक्रमण और [[ग्राफ सिद्धांत]] सम्मलित होते है। चाप एक स्थान से संक्रमण या इसके विपरीत चलते है, स्थानों के बीच या संक्रमण के बीच कभी नहीं चलते है। जिन स्थानों से चाप एक संक्रमण तक चलता है उन्हें संक्रमण के इनपुट स्थान कहा जाता है, जिन स्थानों पर संक्रमण से चाप चलते है उन्हें संक्रमण के आउटपुट स्थान कहा जाता है। | |||
ग्राफिक रूप से, पेट्री नेट में स्थानों में असतत संख्या में चिह्न हो सकते | ग्राफिक रूप से, पेट्री नेट में स्थानों में असतत संख्या में चिह्न हो सकते है जिन्हें टोकन कहा जाता है। स्थानों पर टोकन का कोई भी वितरण अंकन कहे जाने वाले नेट के विन्यास का प्रतिनिधित्व करता है। पेट्री नेट आरेख से संबंधित एक अमूर्त अर्थ में, पेट्री नेट का एक संक्रमण सक्रिय हो सकता है यदि यह सक्षम है, अर्थात इसके सभी इनपुट स्थानों में पर्याप्त टोकन है, जब संक्रमण प्रारंभ होता है, तो यह आवश्यक इनपुट टोकन का उपभोग करता है, और इसके आउटपुट स्थानों में टोकन बनाता है। | ||
जब तक एक निष्पादन नीति (उदाहरण के लिए संक्रमणों का एक सख्त क्रम, पूर्वता का वर्णन) परिभाषित नहीं किया जाता है, पेट्री नेट का निष्पादन गैर-नियतात्मक है: जब एक ही समय में कई संक्रमण सक्षम होते | जब तक एक निष्पादन नीति (उदाहरण के लिए संक्रमणों का एक सख्त क्रम, पूर्वता का वर्णन) परिभाषित नहीं किया जाता है, पेट्री नेट का निष्पादन गैर-नियतात्मक होता है: जब एक ही समय में कई संक्रमण सक्षम होते है, तो वे किसी भी क्रम में सक्रिय हो जाते है। | ||
चूंकि फायरिंग गैर-नियतात्मक है, और कई टोकन नेट में कहीं भी | चूंकि फायरिंग गैर-नियतात्मक है, और कई टोकन नेट में कहीं भी उपस्तिथ हो सकते है (यहां तक कि एक ही स्थान पर), पेट्री नेट वितरित प्रणाली के समवर्ती व्यवहार के मॉडलिंग के लिए उपयुक्त होती है। | ||
== औपचारिक परिभाषा और बुनियादी शब्दावली == | == औपचारिक परिभाषा और बुनियादी शब्दावली == | ||
पेट्री | पेट्री नेट [[राज्य संक्रमण प्रणाली]] है जो प्राथमिक नेट नामक नेटों के एक वर्ग का विस्तार करती है।<ref>{{cite book | first1 = G. | last1 = Rozenburg | first2 = J. | last2 = Engelfriet | chapter = Elementary Net Systems | editor1-first = W. | editor1-last = Reisig | editor2-first = G. | editor2-last = Rozenberg | title = Lectures on Petri Nets I: Basic Models – Advances in Petri Nets | volume = 1491 | series = Lecture Notes in Computer Science | publisher = Springer | date = 1998 | pages = 12–121 }}</ref> | ||
परिभाषा 1. 'नेट' एक [[टपल]] है <math>N = (P, T, F)</math> जहां | परिभाषा 1. 'नेट' एक [[टपल]] है <math>N = (P, T, F)</math> जहां | ||
# <math>P</math> और <math>T</math> क्रमशः स्थानों और संक्रमणों के असंयुक्त परिमित समुच्चय | # <math>P</math> और <math>T</math> क्रमशः स्थानों और संक्रमणों के असंयुक्त परिमित समुच्चय है। | ||
# <math>F \subseteq (P \times T) \cup (T \times P)</math> (निर्देशित) चापों (या प्रवाह संबंधों) का एक सेट है। | # <math>F \subseteq (P \times T) \cup (T \times P)</math> (निर्देशित) चापों (या प्रवाह संबंधों) का एक सेट है। | ||
'परिभाषा 2.' नेट एन = (पी, टी, एफ) दिया गया है, | 'परिभाषा 2.' नेट एन = (पी, टी, एफ) दिया गया है, विन्यास एक सेट सी है जिससे कि सी <बड़ा>⊆</बड़ा> पी है। | ||
[[File:Petri Net A.jpg|thumb|सक्षम संक्रमण के साथ पेट्री नेट।]][[File:Petri Net B.jpg|thumb|पेट्री नेट जो संक्रमण के बाद | [[File:Petri Net A.jpg|thumb|सक्षम संक्रमण के साथ पेट्री नेट।]][[File:Petri Net B.jpg|thumb|पेट्री नेट जो संक्रमण के बाद प्रारंभ होता है (ऊपर की आकृति में प्रारंभिक पेट्री नेट)।]]परिभाषा 3. एक ''प्रारंभिक नेट'' ''EN'' = (''N'', ''C'') रूप का नेट है जहां | ||
# ''N'' = (''P'', ''T'', ''F'') एक | # ''N'' = (''P'', ''T'', ''F'') एक नेट है। | ||
#'सी' ऐसा है कि ''सी'' <बड़ा>⊆</बड़ा> ''पी'' एक '' | #'सी' ऐसा है कि ''सी'' <बड़ा>⊆</बड़ा> ''पी'' एक ''विन्यास'' है। | ||
परिभाषा 4. | परिभाषा 4. पेट्री नेट ''पीएन'' = (''एन'', ''एम'', ''डब्ल्यू'') के रूप का नेट है, जो प्राथमिक नेट का विस्तार करता है जिससे कि | ||
# ''N'' = (''P'', ''T'', ''F'') एक | # ''N'' = (''P'', ''T'', ''F'') एक नेट है। | ||
# ''M'' : ''P'' <big>→</big> ''Z'' एक जगह [[ multiset | मल्टीसेट]] | # ''M'' : ''P'' <big>→</big> ''Z'' एक जगह [[ multiset |मल्टीसेट]] है, जहां ''Z'' एक [[ गणनीय सेट |गणनीय सेट]] है। ''एम'' ''विन्यास'' की अवधारणा का विस्तार करता है और इसे सामान्यतः पेट्री नेट डायग्राम के संदर्भ में ''मार्किंग'' के रूप में वर्णित किया जाता है। | ||
# ''W'' : ''F'' <big>→</big> ''Z'' एक चाप मल्टीसेट है, | # ''W'' : ''F'' <big>→</big> ''Z'' एक चाप मल्टीसेट है, जिससे कि प्रत्येक चाप के लिए गिनती (या वजन) चाप की बहुलता का माप किया जाता है। | ||
यदि | यदि पेट्री नेट एक प्राथमिक नेट के बराबर है, तो ''Z'' काउंटेबल सेट {0,1} हो सकता है और ''P'' में वे तत्व जो ''M'' के अनुसार 1 को मैप करते है, एक विन्यास बनाते है। इसी तरह, यदि पेट्री नेट प्राथमिक नेट नहीं है, तो मल्टीसेट ''M'' की व्याख्या विन्यास के गैर-सिंगलटन सेट का प्रतिनिधित्व करने के रूप में की जा सकती है। इस संबंध में, 'एम' पेट्री नेट के लिए प्रारंभिक नेट के लिए विन्यास की अवधारणा का विस्तार करता है। | ||
पेट्री नेट के आरेख में | पेट्री नेट के आरेख में, स्थानों को पारंपरिक रूप से मंडलियों के साथ चित्रित किया गया है, लंबे संकीर्ण आयतों के साथ संक्रमण और एक तरफा तीर के रूप में चाप जो स्थानों के संक्रमण या संक्रमण के स्थानों के कनेक्शन दिखाते है। यदि आरेख एक प्राथमिक नेट का होता है, तो विन्यास में उन स्थानों को पारंपरिक रूप से मंडलियों के रूप में दर्शाया जाता है, जहां प्रत्येक वृत्त में एक बिंदु सम्मलित होता है जिसे टोकन कहा जाता है। पेट्री नेट के दिए गए आरेख में, स्थान चक्रों में एक से अधिक टोकन सम्मलित हो सकते है, यह दिखाने के लिए कि विन्यास में कोई स्थान कितनी बार दिखाई देता है। संपूर्ण पेट्री नेट आरेख पर वितरित टोकन के विन्यास को अंकन कहा जाता है। | ||
शीर्ष आकृति में (दाएं देखें), स्थान | शीर्ष आकृति में (दाएं देखें), स्थान p1 संक्रमण t का एक इनपुट स्थान है, जबकि, स्थान p2 उसी संक्रमण के लिए एक आउटपुट स्थान है। बता दें कि ''P''N0 (ऊपरी आकृति) कॉन्फ़िगर किए गए ''M''0 के साथ पेट्री नेट है, और ''P''N1 (नीचे का आंकड़ा) कॉन्फ़िगर किए गए ''M''1 के साथ पेट्री नेट है। ''P''N0 का विन्यास संपत्ति के माध्यम से संक्रमण टी को सक्षम करता है कि सभी इनपुट स्थानों में टोकन की पर्याप्त संख्या होती है। केवल एक बार संक्रमण सक्षम हो जाने पर संक्रमण सक्रिय हो जाता है। इस उदाहरण में, संक्रमण टी की फायरिंग एक नक्शा उत्पन्न करती है जिसमें ''M''0 की छवि में मार्किंग कॉन्फ़िगर किया गया ''M''1 होता है और पेट्री नेट ''P''N1 में परिणाम होता है, जो नीचे की आकृति में देखा जाता है। आरेख में, एक संक्रमण के लिए फायरिंग नियम को इसके इनपुट स्थानों से संबंधित इनपुट चाप्स की बहुलता के बराबर कई टोकन घटाकर और संबंधित की बहुलता के बराबर आउटपुट स्थानों पर टोकन की एक नई संख्या जमा करके चित्रित किया जा सकता है। | ||
टिप्पणी 1. "बराबर या अधिक" का त्रुटिहीन अर्थ फायरिंग नियम में Z पर लागू होने वाले जोड़ के त्रुटिहीन बीजगणितीय गुणों पर निर्भर करेगा, जहां बीजगणितीय गुणों पर सूक्ष्म भिन्नताएं पेट्री नेट के अन्य वर्गों को जन्म दे सकती है, उदाहरण के लिए, बीजगणितीय पेट्री नेट।<ref>{{cite journal | last1 = Reisig | first1 = Wolfgang | date = 1991 | title = पेट्री नेट और बीजगणितीय विनिर्देश| journal = Theoretical Computer Science | volume = 80 | issue = 1| pages = 1–34 | doi=10.1016/0304-3975(91)90203-e| doi-access = free }}</ref> | |||
निम्नलिखित औपचारिक परिभाषा शिथिल रूप से {{harv|पीटरसन|1981}} पर आधारित है। कई वैकल्पिक परिभाषाएँ उपस्तिथ है। | |||
निम्नलिखित औपचारिक परिभाषा शिथिल रूप से | |||
=== | === वाक्य - विन्यास === | ||
पेट्री नेट ग्राफ (कुछ लोगों द्वारा ''पेट्री नेट'' कहा जाता है, लेकिन नीचे देखें) एक 3-टपल है <math>(S,T,W)</math>, जहाँ | |||
* S स्थानों का परिमित समुच्चय है | * S स्थानों का परिमित समुच्चय है | ||
* T संक्रमणों का परिमित समुच्चय है | * T संक्रमणों का परिमित समुच्चय है | ||
* S और T असंयुक्त समुच्चय | * S और T असंयुक्त समुच्चय है, अर्थात कोई भी वस्तु स्थान और संक्रमण दोनों नहीं हो सकती | ||
* <math>W: (S \times T) \cup (T \times S) \to \mathbb{N}</math> निर्देशित किनारों का एक मल्टीसेट है, | * <math>W: (S \times T) \cup (T \times S) \to \mathbb{N}</math> निर्देशित किनारों का एक मल्टीसेट है, अर्थात यह प्रत्येक चाप को एक गैर-नकारात्मक पूर्णांक चाप बहुलता (या वजन) प्रदान करता है, ध्यान दें कि कोई चाप दो स्थानों या दो संक्रमणों को नहीं जोड़ सकता है। | ||
प्रवाह संबंध चापों का समुच्चय है: <math> F = \{ (x,y) \mid W(x,y) > 0 \}</math>. कई पाठ्यपुस्तकों में, चापों में केवल बहुलता हो सकती है। ये पाठ | प्रवाह संबंध चापों का समुच्चय है: <math> F = \{ (x,y) \mid W(x,y) > 0 \}</math>. कई पाठ्यपुस्तकों में, चापों में केवल बहुलता हो सकती है। ये पाठ अधिकांशतः W के अतिरिक्त F का उपयोग करके पेट्री नेट को परिभाषित करते है। इस सम्मेलन का उपयोग करते समय, पेट्री नेट ग्राफ एक द्विदलीय ग्राफ [[मल्टीग्राफ]] होता है। <math>(S \cup T, F)</math> नोड विभाजन एस और टी के साथ होता है। | ||
संक्रमण t का प्रीसेट इसके इनपुट स्थानों का सेट है: <math>{}^{\bullet}t = \{ s \in S \mid W(s,t) > 0 \}</math>; | |||
इसका पोस्टसेट इसके आउटपुट स्थानों का सेट है: <math>t^{\bullet} = \{ s \in S \mid W(t,s) > 0 \}</math>. स्थानों के पूर्व और बाद के सेट की परिभाषाएं समान है। | |||
एक 'पेट्री नेट' (कुछ लोगों द्वारा चिह्नित पेट्री नेट कहा जाता है, ऊपर देखें) एक 4-ट्यूपल है <math>(S,T,W,M_0)</math>, | पेट्री नेट (ग्राफ) का एक अंकन इसके स्थानों का एक मल्टीसेट है, अर्थात मैपिंग <math>M: S \to \mathbb{N}</math>. हम कहते है कि अंकन प्रत्येक स्थान को कई टोकन प्रदान करता है। | ||
* <math>(S,T,W)</math> पेट्री नेट ग्राफ है | |||
* <math>M_0</math> प्रारंभिक अंकन है, पेट्री नेट ग्राफ का | एक 'पेट्री नेट' (कुछ लोगों द्वारा चिह्नित पेट्री नेट कहा जाता है, ऊपर देखें) एक 4-ट्यूपल है <math>(S,T,W,M_0)</math>, जहाँ | ||
* <math>(S,T,W)</math> पेट्री नेट ग्राफ है, | |||
* <math>M_0</math> प्रारंभिक अंकन है, पेट्री नेट ग्राफ का अंकन है। | |||
=== निष्पादन शब्दार्थ === | === निष्पादन शब्दार्थ === | ||
शब्दों में | शब्दों में | ||
* एक संक्रमण फायरिंग {{mvar|t}} अंकन में {{mvar|M}} खपत करता है <math>W(s,t)</math> इसके प्रत्येक इनपुट स्थान से टोकन {{mvar|s}}, और | * एक संक्रमण फायरिंग {{mvar|t}} अंकन में {{mvar|M}} खपत करता है <math>W(s,t)</math> इसके प्रत्येक इनपुट स्थान से टोकन {{mvar|s}}, और उत्पन्न करता है <math>W(t,s)</math> इसके प्रत्येक आउटपुट स्थानों में टोकन {{mvar|s}} | ||
* एक संक्रमण सक्षम है (यह आग लग सकता है) में {{mvar|M}} यदि इसके इनपुट स्थान में पर्याप्त टोकन | * एक संक्रमण सक्षम है (यह आग लग सकता है) में {{mvar|M}} यदि इसके इनपुट स्थान में पर्याप्त टोकन है तो उपभोग संभव हो सकता है, अर्थात यदि और केवल यदि <math>\forall s: M(s) \geq W(s,t)</math>. | ||
हम | हम सामान्यतः इस बात में रुचि रखते है कि क्या हो सकता है जब संक्रमण मनमाने क्रम में लगातार आग लगा सकता है। | ||
हम कहते | हम कहते है कि एक अंकन {{mvar|M'}} अंकन से पहुंचा जा सकता है {{mvar|M}} यदि एक चरण में <math>M \underset{G}{\longrightarrow} M'</math>, हम कहते है कि यह से पहुंच योग्य है {{mvar|M}} यदि <math>M \overset{*}{\underset{G}{\longrightarrow}} M'</math>, जहाँ <math>\overset{*}{\underset{G}{\longrightarrow}}</math> का स्वतुल्य सकर्मक संवरण है <math>\underset{G}{\longrightarrow}</math>; अर्थात, यदि यह 0 या अधिक चरणों में पहुंचा जा सकता है। | ||
एक (चिह्नित) पेट्री नेट के लिए <math>N=(S,T,W,M_0)</math>, हम उन फायरिंग में रुचि रखते | एक (चिह्नित) पेट्री नेट के लिए <math>N=(S,T,W,M_0)</math>, हम उन फायरिंग में रुचि रखते है जिन्हें प्रारंभिक मार्किंग से प्रारंभ किया जा सकता है <math>M_0</math>. इसके पहुंच योग्य चिह्नों का सेट है <math>R(N) \ \stackrel{D}{=}\ \left\{ M' \Bigg| M_0 \xrightarrow[(S,T,W)]{*} M' \right\} </math> पहुंच योग्यता ग्राफ {{mvar|N}} संक्रमण संबंध है <math>\underset{G}{\longrightarrow}</math> इसके पहुंच योग्य चिह्नों तक ही सीमित है <math>R(N)</math>. यह नेट का [[ राज्य अंतरिक्ष |राज्य अंतरिक्ष]] है। | ||
<math>R(N) \ \stackrel{D}{=}\ \left\{ M' \Bigg| M_0 \xrightarrow[(S,T,W)]{*} M' \right\} </math> | |||
पहुंच योग्यता ग्राफ {{mvar|N}} संक्रमण संबंध है <math>\underset{G}{\longrightarrow}</math> इसके पहुंच योग्य चिह्नों तक ही सीमित है <math>R(N)</math>. यह नेट का [[ राज्य अंतरिक्ष ]] है। | |||
ग्राफ के साथ पेट्री नेट के लिए फायरिंग सीक्वेंस {{mvar|G}} और प्रारंभिक अंकन <math>M_0</math> संक्रमणों का क्रम है <math>\vec \sigma = \langle t_{1} \cdots t_{n} \rangle</math> ऐसा है कि <math>M_0 \underset{G,t_{1}}{\longrightarrow} M_1 \wedge \cdots \wedge M_{n-1} \underset{G,t_{n}}{\longrightarrow} M_n</math>. फायरिंग सीक्वेंस के सेट को इस रूप में दर्शाया गया है <math>L(N)</math>. | ग्राफ के साथ पेट्री नेट के लिए फायरिंग सीक्वेंस {{mvar|G}} और प्रारंभिक अंकन <math>M_0</math> संक्रमणों का क्रम है <math>\vec \sigma = \langle t_{1} \cdots t_{n} \rangle</math> ऐसा है कि <math>M_0 \underset{G,t_{1}}{\longrightarrow} M_1 \wedge \cdots \wedge M_{n-1} \underset{G,t_{n}}{\longrightarrow} M_n</math>. फायरिंग सीक्वेंस के सेट को इस रूप में दर्शाया गया है <math>L(N)</math>. | ||
== परिभाषा पर बदलाव == | == परिभाषा पर बदलाव == | ||
चाप बहुलता को अस्वीकार करने और चाप डब्ल्यू के बैग को एक साधारण सेट के साथ बदलने के लिए एक सामान्य भिन्नता है, जिसे प्रवाह संबंध कहा जाता है, <math>F \subseteq (S \times T) \cup (T \times S)</math>. | |||
एक | यह [[अभिव्यंजक शक्ति (कंप्यूटर विज्ञान)]] को सीमित नहीं करता है क्योंकि दोनों एक दूसरे का प्रतिनिधित्व कर सकते है। | ||
देसेल और जुहास (2001) में,<ref>{{cite book | last1 = Desel | first1 = Jörg | last2 = Juhás | first2 = Gabriel | chapter = What Is a Petri Net? Informal Answers for the Informed Reader | editor1-first = Hartmut | editor1-last = Ehrig | editor1-link=Hartmut Ehrig| title = पेट्री नेट्स को एकीकृत करना| series = LNCS | volume = 2128 | pages = 1–25 | date = 2001 |publisher=Springer | doi = 10.1007/3-540-45541-8_1 |display-editors=etal| isbn = 9783540430674 }}</ref> क्षमता को स्थानों पर परिभाषित करने की अनुमति दिया था। इस पर नीचे विस्तार के अनुसार चर्चा की गई है। | |||
== सदिशों और आव्यूहों के संदर्भ में निरूपण == | == सदिशों और आव्यूहों के संदर्भ में निरूपण == | ||
| Line 95: | Line 94: | ||
* <math> W^T = - W^- + W^+</math> | * <math> W^T = - W^- + W^+</math> | ||
मैट्रिक्स गुणा के संदर्भ में पहुंच योग्य चिह्नों का वर्णन करने के लिए निम्नानुसार उपयोग किया जा सकता है। | मैट्रिक्स गुणा के संदर्भ में पहुंच योग्य चिह्नों का वर्णन करने के लिए निम्नानुसार उपयोग किया जा सकता है। | ||
संक्रमण के किसी भी क्रम के लिए {{mvar|w}}, लिखना <math>o(w)</math> वेक्टर के लिए जो प्रत्येक संक्रमण को इसकी घटनाओं की संख्या में मैप करता है {{mvar|w}}. तो हमारे पास | |||
* <math>R(N) = \{ M \mid \exists w:\ w \text{ is a firing sequence of } N\ \text{ and }\ M = M_0 + W^T \cdot o(w) \}</math>. | संक्रमण के किसी भी क्रम के लिए {{mvar|w}}, लिखना <math>o(w)</math> वेक्टर के लिए जो प्रत्येक संक्रमण को इसकी घटनाओं की संख्या में मैप करता है {{mvar|w}}. तो हमारे पास है | ||
यह आवश्यक होना चाहिए {{mvar|w}} फायरिंग सीक्वेंस है | * <math>R(N) = \{ M \mid \exists w:\ w \text{ is a firing sequence of } N\ \text{ and }\ M = M_0 + W^T \cdot o(w) \}</math>. | ||
यह आवश्यक होना चाहिए {{mvar|w}} फायरिंग सीक्वेंस है, संक्रमणों के मनमाना अनुक्रमों की अनुमति देना सामान्यतः एक बड़ा सेट उत्पन्न करता है। | |||
<math display="block"> | <math display="block"> | ||
| Line 103: | Line 103: | ||
W^{+}=\begin{bmatrix} * & t1 & t2 \\ p1 & 0 & 1 \\ p2 & 1 & 0 \\ p3 & 1& 0 \\ p4 & 0 & 1 \end{bmatrix}, \ | W^{+}=\begin{bmatrix} * & t1 & t2 \\ p1 & 0 & 1 \\ p2 & 1 & 0 \\ p3 & 1& 0 \\ p4 & 0 & 1 \end{bmatrix}, \ | ||
W^T=\begin{bmatrix} * & t1 & t2 \\ p1 & -1 & 1 \\ p2 & 1 & -1 \\ p3 & 1 & -1 \\ p4 & 0 & 1 \end{bmatrix} | W^T=\begin{bmatrix} * & t1 & t2 \\ p1 & -1 & 1 \\ p2 & 1 & -1 \\ p3 & 1 & -1 \\ p4 & 0 & 1 \end{bmatrix} | ||
</math> | </math><math display="block"> | ||
<math display="block"> | |||
M_{0}=\begin{bmatrix} 1 & 0 & 2 & 1 \end{bmatrix} | M_{0}=\begin{bmatrix} 1 & 0 & 2 & 1 \end{bmatrix} | ||
</math> | </math> | ||
== श्रेणी-सैद्धांतिक सूत्रीकरण == | == श्रेणी-सैद्धांतिक सूत्रीकरण == | ||
मेसेगुएर और मोंटानारी को एक प्रकार की सममित मोनोइडल श्रेणियां माना जाता है जिन्हें पेट्री श्रेणियों के रूप में जाना जाता है।<ref>{{Cite journal | |||
| title = Petri nets are monoids | | title = Petri nets are monoids | ||
| first1 = Jose | last1 = Meseguer | | first1 = Jose | last1 = Meseguer | ||
| Line 126: | Line 121: | ||
| doi-access = free | | doi-access = free | ||
}}</ref> | }}</ref> | ||
== पेट्री नेट के गणितीय गुण == | == पेट्री नेट के गणितीय गुण == | ||
पेट्री नेट को | पेट्री नेट को रोचक बनाने वाली एक बात यह है कि वे मॉडलिंग शक्ति और विश्लेषण क्षमता के बीच संतुलन प्रदान करते है: पेट्री नेट के लिए समवर्ती प्रणालियों के बारे में बहुत सी चीजें स्वचालित रूप से निर्धारित की जा सकती है, चूंकि उनमें से कुछ चीजें सामान्य रूप से निर्धारित करने के लिए बहुत महंगी होती है। पेट्री नेट के कई उपवर्गों का अध्ययन किया गया है जो अभी भी समवर्ती प्रणालियों के रोचक वर्गों का मॉडल बना सकते है, जबकि ये समस्याएं आसान हो जाती है। | ||
पेट्री नेट और कुछ उपवर्गों के लिए निर्णायकता और जटिलता परिणामों के साथ इस तरह की [[निर्णय समस्या|निर्णय समस्याओं]] का अवलोकन एस्पार्ज़ा और नीलसन (1995) में पाया जा सकता है।<ref>{{cite journal | url = http://citeseer.ist.psu.edu/226920.html | title = Decidability issues for Petri nets – a survey | first1 = Javier | last1 = Esparza | first2 = Mogens | last2 = Nielsen | journal = Bulletin of the EATCS | orig-year = 1994 | edition = Revised | date = 1995 |access-date=2014-05-14}}</ref> | |||
=== | === गम्यता === | ||
पेट्री नेट के लिए रीचबिलिटी की समस्या यह तय करना है कि पेट्री नेट एन और मार्किंग एम दिया गया है या नहीं <math>M \in R(N)</math>. | पेट्री नेट के लिए रीचबिलिटी की समस्या यह तय करना है कि पेट्री नेट एन और मार्किंग एम दिया गया है या नहीं <math>M \in R(N)</math>. | ||
यह ऊपर परिभाषित | यह ऊपर परिभाषित गम्यता-ग्राफ चलने की स्थिति है, जब तक या अनुरोधित-अंकन नहीं हो जाता है या अब नहीं मिल सकता है। यह पहले की तुलना में कठिन है: गम्यता ग्राफ सामान्यतः अनंत है, और यह निर्धारित करना आसान नहीं है कि कब रुकना सुरक्षित है। | ||
वास्तव में, इस समस्या को [[EXPSPACE]]-कठिन दिखाया गया था<ref>{{cite journal | last = Lipton | first = R. | url = http://citeseer.ist.psu.edu/contextsummary/115623/0 | title = रीचैबिलिटी प्रॉब्लम के लिए एक्सपोनेंशियल स्पेस की आवश्यकता होती है| journal = Technical Report 62 | date = 1976 }}</ref> सालों पहले इसे बिल्कुल भी निर्णायक दिखाया गया था (मेयर, 1981)। इसे कुशलतापूर्वक कैसे किया जाए, इस पर शोध पत्र प्रकाशित होते रहते | वास्तव में, इस समस्या को [[EXPSPACE|एक्सपस्पेस]]-कठिन दिखाया गया था<ref>{{cite journal | last = Lipton | first = R. | url = http://citeseer.ist.psu.edu/contextsummary/115623/0 | title = रीचैबिलिटी प्रॉब्लम के लिए एक्सपोनेंशियल स्पेस की आवश्यकता होती है| journal = Technical Report 62 | date = 1976 }}</ref> सालों पहले इसे बिल्कुल भी निर्णायक दिखाया गया था (मेयर, 1981)। इसे कुशलतापूर्वक कैसे किया जाए, इस पर शोध पत्र प्रकाशित होते रहते है।<ref>{{cite conference | first = P. | last = Küngas | url = http://www.idi.ntnu.no/%7Epeep/papers/SARA2005Kung.ps | title = पेट्री नेट रीचैबिलिटी चेकिंग इज पोलीनॉमियल विथ ऑप्टिमल एब्सट्रैक्शन हायरार्कीज| conference = Proceedings of the 6th International Symposium on Abstraction, Reformulation and Approximation—SARA 2005 | location = Airth Castle, Scotland, UK | date = July 26–29, 2005 | access-date = 10 July 2008 | archive-url = https://web.archive.org/web/20120209084910/http://www.idi.ntnu.no/%7Epeep/papers/SARA2005Kung.ps | archive-date = 9 February 2012 | url-status = dead }}</ref> 2018 में, ज़ेरविंस्की एट अल ने निचली सीमा में सुधार किया और दिखाया कि समस्या [[प्राथमिक]] नहीं है।<ref>{{cite arXiv |eprint=1809.07115|last1=Czerwiński|first1=Wojciech|title=पेट्री नेट्स के लिए रीचैबिलिटी की समस्या प्राथमिक नहीं है (विस्तारित सार)|last2=Lasota|first2=Sławomir|last3=Lazic|first3=Ranko|last4=Leroux|first4=Jerome|last5=Mazowiecki|first5=Filip|class=cs.FL|year=2018}}</ref> 2021 में, जेरोम लेरोक्स द्वारा स्वतंत्र रूप से इस समस्या को गैर-आदिम पुनरावर्ती दिखाया गया था<ref>{{cite arXiv |eprint=2104.12695|last1=Leroux|first1=Jérôme|title=पेट्री नेट्स के लिए रीचैबिलिटी प्रॉब्लम प्रिमिटिव रिकर्सिव नहीं है|class=cs.LO|year=2021}}</ref> और वोज्शिएक ज़ेरविन्स्की और लुकाज़ ऑरलिकोव्स्की द्वारा दिखाया गया था।<ref>{{cite arXiv |eprint=2104.13866|last1=Czerwiński|first1=Wojciech|title=सदिश जोड़ प्रणालियों में पहुंच क्षमता एकरमैन-पूर्ण है|last2=Orlikowski|first2=Łukasz|class=cs.FL|year=2021}}</ref> इस प्रकार ये परिणाम लंबे समय से चली आ रही जटिलता को बंद कर देते है। | ||
जबकि | जबकि गम्यता गलत राज्यों को खोजने के लिए एक अच्छा उपकरण प्रतीत होता है, व्यावहारिक समस्याओं के लिए निर्मित ग्राफ में सामान्यतः गणना करने के लिए बहुत अधिक राज्य होते है। इस समस्या को कम करने के लिए, रैखिक लौकिक तर्क का उपयोग सामान्यतः यह सिद्ध करने के लिए [[विश्लेषणात्मक झांकी की विधि|विश्लेषणात्मक विधि]] के संयोजन में किया जाता है कि ऐसी अवस्थाओं तक नहीं पहुँचा जा सकता है। [[रैखिक लौकिक तर्क]] [[अर्ध-निर्णय प्रक्रिया]] तकनीक का उपयोग यह पता लगाने के लिए करता है कि क्या वास्तव में एक राज्य तक पहुँचा जा सकता है, राज्य तक पहुँचने के लिए आवश्यक शर्तों का एक सेट खोज कर, यह सिद्ध करते हुए कि उन शर्तों को संतुष्ट नहीं किया जा सकता है। | ||
=== सजीवता === | === सजीवता === | ||
[[Image:liveness-levels.gif|thumb|right| | [[Image:liveness-levels.gif|thumb|right|पेट्री नेट जिसमें संक्रमण होता है <math>t_0</math> मर चुका है, जबकि सभी के लिए <math>j>0,</math> <math>t_j</math> है <math>L_j</math>-रहना]]पेट्री नेट को जीवंतता की विभिन्न डिग्री के रूप में वर्णित किया जा सकता है <math>L_1 - L_4</math>. वह पेट्री नेट <math>(N, M_0)</math> कहा जाता है <math>L_k</math>-जीएं [[अगर और केवल अगर|और केवल यदि]] इसके सभी संक्रमण है <math>L_k</math>-लाइव, जहां एक संक्रमण है | ||
* मृत, | * मृत, यदि यह कभी भी फायर नहीं कर सकता है, अर्थात यह फायरिंग सीक्वेंस में नहीं है <math>L(N,M_0)</math> | ||
* <math>L_1</math>-लाइव (संभावित रूप से फायर करने योग्य), | * <math>L_1</math>-लाइव (संभावित रूप से फायर करने योग्य), यदि और केवल यदि यह फायर कर सकता है, अर्थात यह कुछ फायरिंग सीक्वेंस में है <math>L(N,M_0)</math> | ||
* <math>L_2</math>-Live | * <math>L_2</math>-Live यदि यह मनमाने ढंग से अधिकांशतः आग लगा सकता है, अर्थात यदि हर सकारात्मक पूर्णांक के लिए {{mvar|k}}, यह कम से कम होता है {{mvar|k}} बार कुछ फायरिंग सीक्वेंस में है <math>L(N,M_0)</math> | ||
* <math>L_3</math>-लाइव | * <math>L_3</math>-लाइव यदि यह असीम रूप से अधिकांशतः आग लगा सकता है, अर्थात यदि कुछ निश्चित (आवश्यक अनंत) फायरिंग अनुक्रम है जिसमें प्रत्येक सकारात्मक पूर्णांक के लिए {{mvar|k}}, संक्रमण <math>L_3</math> कम से कम होता है {{mvar|k}}, | ||
* <math>L_4</math>-लाइव (लाइव) | * <math>L_4</math>-लाइव (लाइव) यदि यह हमेशा आग लगा सकता है, अर्थात यह है <math>L_1</math>में हर पहुंच योग्य अंकन में रहते है <math>R(N,M_0)</math> | ||
ध्यान दें कि ये तेजी से कठोर आवश्यकताएं | ध्यान दें कि ये तेजी से कठोर आवश्यकताएं है: <math>L_{j+1}</math>-जीवंतता का तात्पर्य है <math>L_j</math>-जीवंतता, के लिए है <math display="inline">\textstyle{j \in {1,2,3}}</math>. | ||
ये परिभाषाएँ मुराता के अवलोकन के अनुसार | ये परिभाषाएँ मुराता के अवलोकन के अनुसार है,<ref>{{cite journal | url = http://www.cs.uic.edu/bin/view/Murata/Publications | title = Petri Nets: Properties, Analysis and Applications | first = Tadao | last = Murata | journal = Proceedings of the IEEE | volume = 77 | issue = 4 | pages = 541–558 | date = April 1989 | access-date = 2014-10-13 | doi=10.1109/5.24143}}</ref> जो अतिरिक्त रूप से उपयोग करता है <math>L_0</math>-मृत के लिए एक शब्द के रूप में जीना होता है। | ||
=== सीमाबद्धता === | === सीमाबद्धता === | ||
[[File:Reachability graph for petri net.png|right|frame| | [[File:Reachability graph for petri net.png|right|frame|एन2 का रीचेबिलिटी ग्राफ।]]पेट्री नेट में एक जगह को के-बाउंड कहा जाता है यदि इसमें प्रारंभिक अंकन सहित सभी पहुंच योग्य चिह्नों में के टोकन से अधिक नहीं होते है, यदि यह 1-बाध्य है तो इसे सुरक्षित कहा जाता है, यह परिबद्ध है यदि यह कुछ k के लिए k-बाध्य है। | ||
ए (चिन्हित) पेट्री नेट को के-बाउंडेड, सेफ या बाउंडेड कहा जाता है जब इसके सभी स्थान होते | ए (चिन्हित) पेट्री नेट को के-बाउंडेड, सेफ या बाउंडेड कहा जाता है जब इसके सभी स्थान होते है। पेट्री नेट (ग्राफ) को (संरचनात्मक रूप से) बाउंडेड कहा जाता है यदि यह हर संभव प्रारंभिक अंकन के लिए बाउंड होता है। | ||
पेट्री नेट बंधा हुआ है केवल यदि इसकी गम्यता ग्राफ परिमित होता है। | |||
[[रिचर्ड कार्प]]-मिलर ट्री का निर्माण करके, कवरिंग समस्या को देखते हुए बाउंडेडनेस निर्णायक है। | [[रिचर्ड कार्प]]-मिलर ट्री का निर्माण करके, कवरिंग समस्या को देखते हुए बाउंडेडनेस निर्णायक होता है। | ||
किसी दिए गए | किसी दिए गए नेट में स्थानों पर स्पष्ट रूप से बाध्य होना उपयोगी हो सकता है। इसका उपयोग सीमित प्रणाली संसाधनों को मॉडल करने के लिए किया जा सकता है। | ||
इसका उपयोग सीमित | |||
पेट्री नेट की कुछ परिभाषाएँ स्पष्ट रूप से इसे एक वाक्यगत विशेषता के रूप में अनुमति | पेट्री नेट की कुछ परिभाषाएँ स्पष्ट रूप से इसे एक वाक्यगत विशेषता के रूप में अनुमति देता है।<ref> | ||
{{cite web | {{cite web | ||
|url=http://www.techfak.uni-bielefeld.de/~mchen/BioPNML/Intro/pnfaq.html | |url=http://www.techfak.uni-bielefeld.de/~mchen/BioPNML/Intro/pnfaq.html | ||
| Line 173: | Line 162: | ||
|website = www.techfak.uni-bielefeld.de | |website = www.techfak.uni-bielefeld.de | ||
}} | }} | ||
</ref> | </ref> औपचारिक रूप से, स्थान क्षमता वाले पेट्री नेट को टुपल्स के रूप में परिभाषित किया जा सकता है <math>(S,T,W,C,M_0)</math>, कहाँ <math>(S,T,W,M_0)</math> पेट्री नेट है, <math>C: P \rightarrow\!\!\!\shortmid \mathbb N</math> (कुछ या सभी) स्थानों के लिए क्षमताओं का एक असाइनमेंट, और संक्रमण संबंध सामान्य रूप से चिह्नों तक सीमित होता है जिसमें क्षमता वाले प्रत्येक स्थान पर अधिक से अधिक कई टोकन होते है। | ||
औपचारिक रूप से, स्थान क्षमता वाले पेट्री | |||
[[File:Two-boundedness-ub.png|right|frame|एक असीमित पेट्री नेट, एन।]]उदाहरण के लिए, यदि नेट N में, दोनों स्थानों को क्षमता 2 निर्दिष्ट की गई है, तो हम स्थान क्षमताओं के साथ पेट्री नेट प्राप्त करते | [[File:Two-boundedness-ub.png|right|frame|एक असीमित पेट्री नेट, एन।]]उदाहरण के लिए, यदि नेट N में, दोनों स्थानों को क्षमता 2 निर्दिष्ट की गई है, तो हम स्थान क्षमताओं के साथ पेट्री नेट प्राप्त करते है, N2 कहते है, इसका गम्यता ग्राफ दाईं ओर प्रदर्शित होती है। | ||
[[File:Two-boundedness-cb.png|right|frame|काउंटर-प्लेस के साथ एन का विस्तार करके प्राप्त एक दो-बाउंड पेट्री नेट।]]वैकल्पिक रूप से, | [[File:Two-boundedness-cb.png|right|frame|काउंटर-प्लेस के साथ एन का विस्तार करके प्राप्त एक दो-बाउंड पेट्री नेट।]]वैकल्पिक रूप से, नेट को फैलाकर स्थानों को घेरा जा सकता है। त्रुटिहीन होने के लिए, स्थान के विपरीत प्रवाह के साथ "काउंटर-प्लेस" जोड़कर और दोनों स्थानों में कुल बनाने के लिए टोकन जोड़कर एक जगह को के-बाध्य बनाया जा सकता है। | ||
== असतत, निरंतर और संकर पेट्री नेट == | |||
साथ ही असतत घटनाओं के लिए, निरंतर और संकर असतत-निरंतर प्रक्रियाओं के लिए पेट्री नेट होता है<ref name=":0" />जो असतत, सतत और संकर [[नियंत्रण सिद्धांत]] में उपयोगी होते है,<ref name="DavidAlla2005">{{cite book | url = https://books.google.com/books?id=VsS0JkMcXGwC | title = असतत, निरंतर और हाइब्रिड पेट्री नेट्स| first1 = René | last1 = David | first2 = Hassane | last2 = Alla | publisher = Springer | date = 2005 | isbn = 978-3-540-22480-8 }}</ref> और असतत, निरंतर और संकर [[ऑटोमेटा सिद्धांत]] से संबंधित होते है। | |||
== असतत, निरंतर | |||
साथ ही असतत घटनाओं के लिए, निरंतर और संकर असतत-निरंतर प्रक्रियाओं के लिए पेट्री | |||
== एक्सटेंशन == | == एक्सटेंशन == | ||
पेट्री नेट्स के कई विस्तार | पेट्री नेट्स के कई विस्तार है। उनमें से कुछ मूल पेट्री नेट के साथ पूरी तरह से पीछे की ओर-संगत (जैसे [[रंगीन पेट्री जाल|रंगीन पेट्री नेट]]) है, कुछ ऐसे गुण जोड़ते है जिन्हें मूल पेट्री नेट औपचारिकता (जैसे समयबद्ध पेट्री नेट) में मॉडल नहीं किया जा सकता है। चूंकि पश्च-संगत मॉडल पेट्री नेट की कम्प्यूटेशनल शक्ति का विस्तार नहीं करते है, उनके पास अधिक संक्षिप्त प्रतिनिधित्व हो सकते है और मॉडलिंग के लिए अधिक सुविधाजनक हो सकते है।<ref>{{cite book|last1=Jensen|first1=Kurt|author-link= Kurt Jensen (computer scientist)|title=रंगीन पेट्री जालों का संक्षिप्त परिचय|volume=1217|pages=203–208|chapter-url=https://link.springer.com/content/pdf/10.1007/BFb0035389.pdf|doi=10.1007/BFb0035389|chapter=A brief introduction to coloured Petri Nets|series=Lecture Notes in Computer Science|year=1997|isbn=978-3-540-62790-6}}</ref> एक्सटेंशन जिन्हें पेट्री नेट में परिवर्तित नहीं किया जा सकता है, कभी-कभी बहुत शक्तिशाली होते है, लेकिन सामान्यतः सामान्य पेट्री नेट का विश्लेषण करने के लिए उपलब्ध गणितीय उपकरणों की पूरी श्रृंखला का अभाव होता है। | ||
[[उच्च स्तरीय पेट्री नेट]] शब्द का प्रयोग कई पेट्री नेट औपचारिकताओं के लिए किया जाता है जो बुनियादी पी/टी नेट औपचारिकता का विस्तार करते | [[उच्च स्तरीय पेट्री नेट]] शब्द का प्रयोग कई पेट्री नेट औपचारिकताओं के लिए किया जाता है जो बुनियादी पी/टी नेट औपचारिकता का विस्तार करते है, इसमें रंगीन पेट्री नेट, पदानुक्रमित पेट्री नेट जैसे नेट के भीतर नेट, और इस खंड में स्केच किए गए अन्य सभी विस्तार सम्मलित होते है। इस शब्द का प्रयोग विशेष रूप से [[ सीपीएन उपकरण |सीपीएन उपकरण]] द्वारा समर्थित रंगीन नेटों के प्रकार के लिए भी किया जाता है। | ||
संभावित एक्सटेंशन की एक छोटी सूची इस प्रकार है: | संभावित एक्सटेंशन की एक छोटी सूची इस प्रकार है: | ||
* अतिरिक्त प्रकार के चाप | * अतिरिक्त प्रकार के चाप, दो सामान्य प्रकार है | ||
** एक रीसेट | ** एक रीसेट चाप फायरिंग पर कोई पूर्व शर्त नहीं लगाता है, और संक्रमण के प्रारंभ होने पर जगह को खाली कर देता है, यह पहुंच योग्यता को अनिर्णीत बनाता है,<ref>{{cite journal | first1 = T. | last1 = Araki | first2 = T. | last2 = Kasami | title = पेट्री नेट्स के लिए रीचैबिलिटी प्रॉब्लम से संबंधित कुछ निर्णय समस्याएं| journal = Theoretical Computer Science | volume = 3 | issue = 1 | pages = 85–104 | date = 1977 | doi=10.1016/0304-3975(76)90067-0| doi-access = free }}</ref> जबकि कुछ अन्य गुण, जैसे समाप्ति, निर्णायक बने रहते है।<ref>{{cite book | first1 = C. | last1 = Dufourd | first2 = A. | last2 = Finkel | first3 = Ph. | last3 =Schnoebelen | chapter = Reset Nets Between Decidability and Undecidability | title = Proceedings of the 25th International Colloquium on Automata, Languages and Programming | series = [[Lecture Notes in Computer Science|LNCS]] | volume = 1443 | pages = 103–115 | date = 1998 }}</ref> | ||
** एक अवरोधक चाप पूर्व शर्त लगाता है कि स्थान खाली होने पर ही संक्रमण | ** एक अवरोधक चाप पूर्व शर्त लगाता है कि स्थान खाली होने पर ही संक्रमण प्रारंभ हो सकता है, यह व्यक्त किए जाने वाले टोकन की संख्या पर मनमाने ढंग से संगणना की अनुमति देता है, जो औपचारिकता [[ट्यूरिंग पूर्ण]] पूर्ण बनाता है और एक सार्वभौमिक नेट के अस्तित्व को दर्शाता है।<ref>{{cite journal | last = Zaitsev | first = D. A. | title = मिनिमल यूनिवर्सल पेट्री नेट की ओर| journal = IEEE Transactions on Systems, Man, and Cybernetics: Systems | date = 2013 | pages = 47–58 | doi = 10.1109/TSMC.2012.2237549 | volume=44| s2cid = 6561556 }}</ref> | ||
* एक मानक पेट्री नेट में, टोकन अप्रभेद्य | * एक मानक पेट्री नेट में, टोकन अप्रभेद्य है। [[रंगीन पेट्री नेट]] में, प्रत्येक टोकन का मूल्य होता है।<ref>{{cite web | url = http://www.daimi.au.dk/CPnets/intro/verybrief.html | title = सीपी-नेट का बहुत संक्षिप्त परिचय| publisher = Department of Computer Science, University of Aarhus, Denmark }}</ref> सीपीएन उपकरण्स जैसे रंगीन पेट्री नेट के लिए लोकप्रिय उपकरण में, टोकन के मूल्यों को टाइप किया जाता है, और इसका परीक्षण किया जा सकता है (गार्ड एक्सप्रेशंस का उपयोग करके) और एक [[कार्यात्मक प्रोग्रामिंग भाषा]] के साथ हेरफेर किया जा सकता है। रंगीन पेट्री नेटों की एक सहायक पेट्री नेट अच्छी तरह से बनाई गई है, जहां नेट का विश्लेषण करना आसान बनाने के लिए चाप और गार्ड अभिव्यक्ति प्रतिबंधित है। | ||
* पेट्री नेट का एक | *पेट्री नेट का एक अन्य लोकप्रिय विस्तार पदानुक्रम है, फेहलिंग द्वारा शोधन और अमूर्तता के समर्थन स्तरों के विभिन्न विचारों के रूप में इसका अध्ययन किया गया था। पदानुक्रम का एक अन्य रूप तथाकथित ऑब्जेक्ट पेट्री नेट या ऑब्जेक्ट प्रणाली में पाया जाता है जहां पेट्री नेट में पेट्री नेट हो सकते है क्योंकि इसके टोकन नेस्टेड पेट्री नेट के पदानुक्रम को प्रेरित करते है जो विभिन्न स्तरों पर संक्रमणों के सिंक्रनाइज़ेशन द्वारा संचार करते है।<ref>{{cite web |url=http://llpn.com/OPNs.html |title=LLPN - रैखिक तर्क पेट्री नेट|access-date=2006-01-06 |url-status=dead |archive-url=https://web.archive.org/web/20051103131745/http://www.llpn.com/OPNs.html |archive-date=2005-11-03 }}</ref> | ||
* एक [[वेक्टर जोड़ प्रणाली]] | *राज्यों (वीएएसएस) के साथ एक [[वेक्टर जोड़ प्रणाली]] पेट्री नेट के समान औपचारिकता है। चूँकि, इसे सतही तौर पर पेट्री नेट के सामान्यीकरण के रूप में देखा जा सकता है। एक [[परिमित राज्य automaton|परिमित राज्य ऑटोमेटन]] पर विचार करें जहां प्रत्येक संक्रमण को पेट्री नेट से संक्रमण द्वारा लेबल किया जाता है। पेट्री नेट को तब परिमित राज्य ऑटोमेटन के साथ सिंक्रनाइज़ किया जाता है, अर्थात, ऑटोमेटन में एक संक्रमण उसी समय लिया जाता है जब पेट्री नेट में संबंधित संक्रमण होता है। पेट्री नेट में संबंधित संक्रमण सक्षम होने पर ही ऑटोमेटन में एक संक्रमण लेना संभव होता है, और पेट्री नेट में एक संक्रमण को आग लगाना केवल तभी संभव है जब इसके द्वारा लेबल किए गए ऑटोमेटन में वर्तमान स्थिति से कोई संक्रमण होता है। (वीएएसएस की परिभाषा सामान्यतः थोड़ी अलग तरीके से तैयार की जाती है।) | ||
* प्राथमिकता वाले पेट्री नेट | * प्राथमिकता वाले पेट्री नेट संक्रमणों में प्राथमिकताएं जोड़ते है, जिससे एक उच्च-प्राथमिकता संक्रमण सक्षम होने पर एक संक्रमण प्रारंभ नहीं हो सकता है (अर्थात आग लगा सकता है)। इस प्रकार, संक्रमण प्राथमिकता समूहों में है, और प्राथमिकता समूह 3 केवल तब सक्रिय हो सकता है जब समूह 1 और 2 में सभी संक्रमण अक्षम होते है। प्राथमिकता समूह के भीतर, फायरिंग अभी भी गैर-निर्धारिती है। | ||
* गैर-नियतात्मक संपत्ति एक बहुत ही मूल्यवान संपत्ति रही है, क्योंकि यह उपयोगकर्ता को बड़ी संख्या में गुणों को सार करने देती | *गैर-नियतात्मक संपत्ति एक बहुत ही मूल्यवान संपत्ति रही है, क्योंकि यह उपयोगकर्ता को बड़ी संख्या में गुणों को सार करने देती है। चूंकि, कुछ स्थितियों में, केवल एक मॉडल की संरचना ही नहीं, जबकि समय को भी मॉडल करने की आवश्यकता होती है। इन स्थितियों के लिए, समयबद्ध पेट्री नेट विकसित हुए है, जहां ऐसे संक्रमण है जो समयबद्ध है, और संभवतः संक्रमण जो समयबद्ध नहीं है (यदि है, तो समयबद्ध संक्रमणों की समयबद्धता की तुलना में उच्च प्राथमिकता है)। समयबद्ध पेट्री नेट की एक सहायक [[ स्टोकेस्टिक पेट्री नेट |स्टोकेस्टिक पेट्री नेट]] है जो संक्रमणों की समायोज्य यादृच्छिकता के माध्यम से गैर-नियतात्मक समय जोड़ता है। घातीय यादृच्छिक वितरण का उपयोग सामान्यतः इन नेटों को 'समय' करने के लिए किया जाता है। इस स्थिति में, नेट गम्यता ग्राफ का उपयोग निरंतर समय [[मार्कोव श्रृंखला]] (सीटीएमसी) के रूप में किया जा सकता है। | ||
* [[द्वैतवादी पेट्री जाल]] (डीपी- | * [[द्वैतवादी पेट्री जाल|द्वैतवादी पेट्री नेट]] (डीपी-नेट) ई. डाविस, एट अल द्वारा विकसित पेट्री नेट एक्सटेंशन है।<ref>{{cite conference | last1 = Dawis | first1 = E. P. | first2 = J. F. | last2 = Dawis | first3 = Wei-Pin | last3 = Koo | date = 2001 | title = द्वैतवादी पेट्री नेट का उपयोग करते हुए कंप्यूटर आधारित प्रणालियों की वास्तुकला| conference = 2001 IEEE International Conference on Systems, Man, and Cybernetics | volume = 3 | pages = 1554–1558 }}</ref> वास्तविक दुनिया की प्रक्रिया का बेहतर प्रतिनिधित्व करने के लिए होती है। डीपी-नेट परिवर्तन/अपरिवर्तन, क्रिया/निष्क्रियता, (परिवर्तन) समय/स्थान आदि के द्वंद्व को संतुलित करते है, परिवर्तन और स्थान के द्विदलीय पेट्री नेट निर्माणों के बीच, जिसके परिणामस्वरूप परिवर्तन अंकन की अनूठी विशेषता होती है, अर्थात, जब परिवर्तन काम कर रहा है यह चिह्नित होता है। यह प्रक्रिया थ्रूपुट के वास्तविक दुनिया के व्यवहार का प्रतिनिधित्व करते हुए कई बार आग (या चिह्नित) के परिवर्तन की अनुमति देता है। परिवर्तन का अंकन मानता है कि परिवर्तन का समय शून्य से अधिक होना चाहिए। कई विशिष्ट पेट्री नेट में उपयोग किया जाने वाला शून्य परिवर्तन समय गणितीय रूप से आकर्षक हो सकता है लेकिन वास्तविक दुनिया की प्रक्रियाओं का प्रतिनिधित्व करने में अव्यावहारिक होता है । डीपी-नेट प्रक्रिया संरचना को चित्रित करने के लिए पेट्री नेट्स के पदानुक्रमित अमूर्तता की शक्ति का भी उपयोग करता है। जटिल प्रक्रिया प्रणालियों को पदानुक्रमित अमूर्तता के विभिन्न स्तरों के माध्यम से परस्पर जुड़े सरल नेटों की एक श्रृंखला के रूप में तैयार किया जाता है। एक पैकेट स्विच के [[ प्रक्रिया वास्तुकला |प्रक्रिया वास्तुकला]] को प्रदर्शित किया जाता है,<ref>{{cite conference | last = Dawis | first = E. P. | date = 2001 | title = Architecture of an SS7 Protocol Stack on a Broadband Switch Platform using Dualistic Petri Nets | conference = 2001 IEEE Pacific Rim Conference on Communications, Computers and signal Processing | volume = 1 | pages = 323–326 }}</ref> जहां डिजाइन प्रणाली की संरचना के आसपास विकास आवश्यकताओं का आयोजन किया जाता है। | ||
पेट्री नेट के कई और विस्तार | पेट्री नेट के कई और विस्तार है, चूंकि, यह ध्यान रखना महत्वपूर्ण है कि जैसे-जैसे विस्तारित गुणों के संदर्भ में नेट की जटिलता बढ़ती है, नेट के कुछ गुणों का मूल्यांकन करने के लिए मानक उपकरणों का उपयोग करना उतना ही कठिन होता है। इस कारण से, किसी दिए गए मॉडलिंग कार्य के लिए सबसे सरल नेट प्रकार का उपयोग करना एक अच्छा विचार होता है। | ||
== प्रतिबंध == | == प्रतिबंध == | ||
[[Image:petri net types.svg|thumb|पेट्री नेट प्रकार रेखांकन]]पेट्री नेट औपचारिकता को विस्तारित करने के | [[Image:petri net types.svg|thumb|पेट्री नेट प्रकार रेखांकन]]पेट्री नेट औपचारिकता को विस्तारित करने के अतिरिक्त, हम इसे प्रतिबंधित करने पर भी देख सकते है, और विशेष प्रकार के पेट्री नेट को देख सकते है, जो एक विशेष तरीके से सिंटैक्स को प्रतिबंधित करके प्राप्त किया जाता है। साधारण पेट्री नेट वे नेट होते है जहां सभी चाप भार 1 होते है। आगे प्रतिबंधित करते हुए, निम्नलिखित प्रकार के साधारण पेट्री नेटों का सामान्यतः उपयोग और अध्ययन किया जाता है: | ||
# एक [[राज्य मशीन]] (एसएम) में, प्रत्येक संक्रमण में एक आने वाली चाप और एक बाहर जाने वाली चाप होती है, और सभी चिह्नों में बिल्कुल एक टोकन होता है। | # एक [[राज्य मशीन]] (एसएम) में, प्रत्येक संक्रमण में एक आने वाली चाप और एक बाहर जाने वाली चाप होती है, और सभी चिह्नों में बिल्कुल एक टोकन होता है। परिणाम स्वरुप, समवर्ती नहीं हो सकता है, लेकिन संघर्ष हो सकता है (अर्थात [[समवर्ती गणना में अनिश्चितता]]): गणितीय रूप से, <math>\forall t\in T: |t^\bullet|=|{}^\bullet t|=1</math> | ||
# एक [[चिह्नित ग्राफ]] (एमजी) में, प्रत्येक स्थान में एक आने वाली चाप और एक बाहर जाने वाली चाप होती है। इसका अर्थ यह है कि विरोध नहीं हो सकता, लेकिन समवर्ती हो सकता है: गणितीय रूप से, <math>\forall s\in S: |s^\bullet|=|{}^\bullet s|=1</math> | # एक [[चिह्नित ग्राफ]] (एमजी) में, प्रत्येक स्थान में एक आने वाली चाप और एक बाहर जाने वाली चाप होती है। इसका अर्थ यह है कि विरोध नहीं हो सकता, लेकिन समवर्ती हो सकता है: गणितीय रूप से, <math>\forall s\in S: |s^\bullet|=|{}^\bullet s|=1</math> | ||
# फ्री चॉइस नेट ( | # फ्री चॉइस नेट (एफसी) में, एक स्थान से एक संक्रमण के लिए प्रत्येक चाप या तो उस स्थान से एकमात्र चाप है या उस संक्रमण के लिए एकमात्र चाप होती है, अर्थात संगामिति और संघर्ष दोनों हो सकते है, लेकिन एक ही समय में नहीं हो सकते है: गणितीय रूप से, <math>\forall s\in S: (|s^\bullet|\leq 1) \vee ({}^\bullet (s^\bullet)=\{s\})</math> | ||
# एक्सटेंडेड फ्री चॉइस ( | # एक्सटेंडेड फ्री चॉइस (ईएफसी) - पेट्री नेट जिसे एफसी में बदला जा सकता है। | ||
# एक असममित विकल्प नेट ( | # एक असममित विकल्प नेट (एसी) में, संगामिति और संघर्ष हो सकता है, लेकिन सममित रूप से नहीं हो सकता है: गणितीय रूप से, <math>\forall s_1,s_2\in S: (s_1{}^\bullet \cap s_2{}^\bullet\neq \emptyset) \to [(s_1{}^\bullet\subseteq s_2{}^\bullet) \vee (s_2{}^\bullet\subseteq s_1{}^\bullet)]</math> | ||
== कार्यप्रवाह नेट == | |||
वर्कफ़्लो नेट (डब्ल्यूएफ-नेट) पेट्री नेट का एक उपवर्ग है जो प्रक्रिया गतिविधियों के वर्कफ़्लो को मॉडल करने का इरादा रखता है।<ref name="Aalst,1998">{{cite journal | last = van der Aalst | first = W. M. P. | date = 1998 | url = http://wwwis.win.tue.nl/~wvdaalst/publications/p53.pdf | title = वर्कफ़्लो प्रबंधन के लिए पेट्री नेट का अनुप्रयोग| journal = Journal of Circuits, Systems and Computers | volume = 8 | issue = 1 | pages = 21–66 | doi=10.1142/s0218126698000043| citeseerx = 10.1.1.30.3125 | s2cid = 248401501 }}</ref> डब्ल्यूएफ-नेट संक्रमण कार्यों या गतिविधियों को सौंपा गया है, और स्थान पूर्व/पोस्ट स्थितियों को असाइन किए गए है। डब्ल्यूएफ-नेट की अतिरिक्त संरचनात्मक और परिचालन आवश्यकताएं होती है, मुख्य रूप से एक एकल इनपुट (स्रोत) स्थान के अतिरिक्त कोई पिछला संक्रमण नहीं है, और आउटपुट स्थान (सिंक) बिना किसी संक्रमण के होता है। तदनुसार, प्रारंभ और समाप्ति चिह्नों को परिभाषित किया जा सकता है जो प्रक्रिया की स्थिति का प्रतिनिधित्व करते है। | |||
- | |||
डब्ल्यूएफ-नेट में ध्वनि प्रॉपर्टी है,<ref name="Aalst,1998" /> यह दर्शाता है कि अपने स्रोत स्थान पर k टोकन के स्टार्ट मार्किंग के साथ एक प्रक्रिया, अपने सिंक स्थान में k टोकन के साथ समापन स्टेट मार्किंग तक पहुँच सकती है (k- ध्वनि डब्ल्यूएफ-नेट के रूप में परिभाषित) इसके अतिरिक्त, प्रक्रिया में सभी संक्रमण लग सकते है (अर्थात, प्रत्येक संक्रमण के लिए एक पहुंच योग्य स्थिति होती है जिसमें संक्रमण सक्षम होता है)। एक सामान्य ध्वनि (जी-ध्वनि) डब्ल्यूएफ-नेट को प्रत्येक के> 0 के लिए के-ध्वनि के रूप में परिभाषित किया गया है।<ref name="Hee et al., 2003">{{cite book | last1 = van Hee | first1 = K. | last2 = Sidorova | first2 = N. | last3 = Voorhoeve | first3 = M. | date = 2003 | chapter-url = http://www.win.tue.nl/~sidorova/03/van_Hee_Sidorova_Voorhoeve.pdf | chapter = Soundness and separability of workflow nets in the stepwise refinement approach | editor1-last = van der Aalst | editor1-first = W. M. P. | editor2-last = Best | editor2-first =E. | title = Application and Theory of Petri Nets 2003 | series = Lect Notes in Comput Sci | volume = 2678 | pages = 337–356 | publisher = Springer }}</ref> | |||
पेट्री नेट में एक निर्देशित [[पथ (ग्राफ सिद्धांत)]] को निर्देशित चापों से जुड़े नोड्स (स्थानों और संक्रमण) के अनुक्रम के रूप में परिभाषित किया गया है। प्राथमिक पथ में अनुक्रम में प्रत्येक नोड केवल एक बार सम्मलित होता है। | |||
एक अच्छी तरह से नियंत्रित पेट्री नेट एक ऐसा नेट है जिसमें एक स्थान और एक संक्रमण (या संक्रमण और एक स्थान) के बीच पूरी तरह से अलग प्राथमिक पथ नहीं होते है, अर्थात, यदि नोड्स की जोड़ी के बीच दो पथ है तो ये पथ एक नोड साझा करते है। एक विश्वकोश अच्छी तरह से नियंत्रित डब्ल्यूएफ-नेट ध्वनि (जी-ध्वनि) होती है।<ref name="Ping et al., 2004">{{cite conference | last1 = Ping | first1 = L. | last2 = Hao | first2 = H. | last3 = Jian | first3 =L. | date = 2004 | title = वर्कफ्लो नेट की 1-सुदृढ़ता और सुदृढ़ता पर| editor-first = Daniel | editor-last = Moldt | conference = Proc of the 3rd Workshop on Modelling of Objects, Components, and Agents | location = Aarhus, Denmark | publisher = DAIMI PB | volume = 571 | pages = 21–36 }}</ref> | |||
विस्तारित डब्ल्यूएफ-नेट पेट्री नेट है जो अतिरिक्त संक्रमण टी (फीडबैक संक्रमण) के साथ डब्ल्यूएफ-नेट से बना होता है। सिंक स्थान संक्रमण टी के इनपुट स्थान और स्रोत स्थान के रूप में इसके आउटपुट स्थान के रूप में जुड़ा हुआ होता है। संक्रमण की फायरिंग प्रक्रिया की पुनरावृत्ति का कारण बनती है।<ref name="Aalst,1998" /> | |||
विस्तारित डब्ल्यूएफ-नेट | |||
डब्ल्यूआरआई डब्ल्यूएफ-नेट, एक विस्तारित एसाइक्लिक अच्छी तरह से हैंडल किया जाने वाला डब्ल्यूएफ-नेट है। डब्ल्यूआरआई-डब्ल्यूएफ-नेट को नेट की संरचना के रूप में बनाया जा सकता है, अर्थात, डब्ल्यूआरआई-डब्ल्यूएफ-नेट के भीतर एक सबनेट के साथ एक संक्रमण को बदलना होता है जो डब्ल्यूआरआई-डब्ल्यूएफ-नेट होता है। नतीजा डब्ल्यूआरआई-डब्ल्यूएफ-net भी होता है। डब्ल्यूआरआई-डब्ल्यूएफ-नेट जी-ध्वनि होती है,<ref name="Ping et al., 2004" /> इसलिए केवल डब्ल्यूआरआई-डब्ल्यूएफ-नेट बिल्डिंग ब्लॉक्स का उपयोग करके, डब्ल्यूएफ-नेट प्राप्त कर सकते है जो निर्माण द्वारा जी-ध्वनि होती है। | |||
[[डिजाइन संरचना मैट्रिक्स]] (डीएसएम) प्रक्रिया संबंधों को मॉडल कर सकता है, और प्रक्रिया नियोजन के लिए उपयोग किया जा सकता है। डीएसएम-नेट, पेट्री नेट द्वारा कार्यप्रवाह प्रक्रियाओं में डीएसएम-आधारित योजनाओं की प्राप्ति करता है, और डब्ल्यूआरआई-डब्ल्यूएफ-नेट के समकक्ष होता है। डीएसएम-नेट निर्माण प्रक्रिया परिणामी नेट की सुदृढ़ता संपत्ति सुनिश्चित करता है। | |||
== समवर्ती के अन्य मॉडल == | |||
मॉडलिंग समवर्ती संगणना के अन्य विधियों का प्रस्ताव किया गया है, जिसमें [[वेक्टर जोड़ प्रणाली]], परिमित-राज्य मशीनों का संचार, क्हान प्रक्रिया नेटवर्क, [[प्रक्रिया बीजगणित]], [[अभिनेता मॉडल]] और [[ट्रेस सिद्धांत]] सम्मलित है।<ref>{{cite book | first = Antoni | last = Mazurkiewicz | chapter = Introduction to Trace Theory | title = निशान की किताब| editor1-first = V. | editor1-last = Diekert | editor2-first = G. | editor2-last = Rozenberg | publisher = World Scientific | location = Singapore | date = 1995 | pages = 3–67 }}</ref> विभिन्न मॉडल [[संरचना]], [[प्रतिरूपकता (प्रोग्रामिंग)]] और स्थानीयता जैसी अवधारणाओं का व्यापार प्रदान करते है। | |||
विन्सेल और नीलसन द्वारा अध्याय में समवर्ती के इन मॉडलों में से कुछ को संबंधित करने का एक दृष्टिकोण प्रस्तावित है।<ref>{{cite book | first1 = G. | last1 = Winskel | first2 = M. | last2 = Nielsen | chapter-url = https://www.cl.cam.ac.uk/~gw104/winskel-nielsen-models-for-concurrency.pdf | chapter = Models for Concurrency | title = हैंडबुक ऑफ़ लॉजिक एंड द फ़ाउंडेशन ऑफ़ कंप्यूटर साइंस| volume = 4 | pages = 1–148 | publisher = OUP | archive-url = https://web.archive.org/web/20200504155703/https://www.cl.cam.ac.uk/~gw104/winskel-nielsen-models-for-concurrency.pdf | archive-date = 4 May 2020 }}</ref> | |||
== उपयेाग क्षेत्र == | |||
* [[बूलियन डिफरेंशियल कैलकुलस]]<ref name="Scheuring_Wehlan_1991_Petri">{{cite journal |title=बूलियन डिफरेंशियल कैलकुलस - पेट्री नेट के विश्लेषण और संश्लेषण के लिए एक विधि|language=de |trans-title=The Boolean differential calculus – A method for analysis and synthesis of Petri nets |first1=Rainer |last1=Scheuring |first2=Herbert "Hans"<!-- This source identifies the author as Herbert Wehlan --> |last2=Wehlan |editor-first=Georg |editor-last=Bretthauer |orig-year=July 1991 |date=1991-12-01 |journal=At – Automatisierungstechnik – Methoden und Anwendungen der Steuerungs-, Regelungs- und Informationstechnik |publisher={{ill|R. Oldenbourg Verlag|de}} |issn=0178-2312 |location=Stuttgart, Germany |volume=39 |number=7 |pages=226–233 |doi=10.1524/auto.1991.39.112.226 |s2cid=56766796 |url=https://www.degruyter.com/view/j/auto.1991.39.issue-1-12/auto.1991.39.112.226/auto.1991.39.112.226.xml |access-date=2017-10-16 |url-status=live |archive-url=https://web.archive.org/web/20171016190403/https://www.degruyter.com/view/j/auto.1991.39.issue-1-12/auto.1991.39.112.226/auto.1991.39.112.226.png |archive-date=2017-10-16}} (8 पृष्ठ)</ref> | |||
* [[बिजनेस प्रोसेस मॉडलिंग]]<ref name="AalstBPM2018">{{cite book |last1=van der Aalst |first1=W.M.P. |title=डेटाबेस सिस्टम्स का विश्वकोश, दूसरा संस्करण|date=2018 |publisher=Springer |url=https://doi.org/10.1007/978-1-4614-8265-9_1179 |chapter=Business Process Management|pages=370–374 |doi=10.1007/978-1-4614-8265-9_1179 |isbn=978-1-4614-8266-6 }}</ref> | |||
* [[कम्प्यूटेशनल बायोलॉजी]]<ref name="Bean 2014">{{cite journal|last=Favrin|first=Bean|title=esyN: Network Building, Sharing and Publishing.|journal=PLOS ONE|date=2 September 2014|pmid=25181461|doi=10.1371/journal.pone.0106035|volume=9|issue=9|pmc=4152123|pages=e106035|bibcode=2014PLoSO...9j6035B|doi-access=free}}</ref><ref>{{cite book |last1=Koch |first1=Ina|author1-link= Ina Koch |last2=Reisig |first2=Wolfgang |last3=Schreiber |first3=Falk |title=सिस्टम बायोलॉजी में मॉडलिंग - पेट्री नेट दृष्टिकोण|series=Computational Biology |date=2011 |volume=16 |publisher=Springer |doi=10.1007/978-1-84996-474-6 |isbn=978-1-84996-473-9 |url=https://dx.doi.org/10.1007/978-1-84996-474-6}}</ref> | * [[कम्प्यूटेशनल बायोलॉजी]]<ref name="Bean 2014">{{cite journal|last=Favrin|first=Bean|title=esyN: Network Building, Sharing and Publishing.|journal=PLOS ONE|date=2 September 2014|pmid=25181461|doi=10.1371/journal.pone.0106035|volume=9|issue=9|pmc=4152123|pages=e106035|bibcode=2014PLoSO...9j6035B|doi-access=free}}</ref><ref>{{cite book |last1=Koch |first1=Ina|author1-link= Ina Koch |last2=Reisig |first2=Wolfgang |last3=Schreiber |first3=Falk |title=सिस्टम बायोलॉजी में मॉडलिंग - पेट्री नेट दृष्टिकोण|series=Computational Biology |date=2011 |volume=16 |publisher=Springer |doi=10.1007/978-1-84996-474-6 |isbn=978-1-84996-473-9 |url=https://dx.doi.org/10.1007/978-1-84996-474-6}}</ref> | ||
* [[समवर्ती प्रोग्रामिंग]]<ref>{{cite conference | first1 = L. M. | last1 = Kristensen | first2 = M. | last2 = Westergaard | title = औद्योगिक महत्वपूर्ण प्रणालियों के लिए औपचारिक तरीके| date = 2010 | chapter = Automatic Structure-Based Code Generation from Coloured Petri Nets: A Proof of Concept | conference = औद्योगिक महत्वपूर्ण प्रणालियों के लिए औपचारिक तरीके- 15th International Workshop, FMICS 2010 | series = Lecture Notes in Computer Science | volume = 6371 | pages = 215–230 | doi = 10.1007/978-3-642-15898-8_14 | isbn = 978-3-642-15897-1 | chapter-url= https://doi.org/10.1007/978-3-642-15898-8_14}}</ref> | * [[समवर्ती प्रोग्रामिंग]]<ref>{{cite conference | first1 = L. M. | last1 = Kristensen | first2 = M. | last2 = Westergaard | title = औद्योगिक महत्वपूर्ण प्रणालियों के लिए औपचारिक तरीके| date = 2010 | chapter = Automatic Structure-Based Code Generation from Coloured Petri Nets: A Proof of Concept | conference = औद्योगिक महत्वपूर्ण प्रणालियों के लिए औपचारिक तरीके- 15th International Workshop, FMICS 2010 | series = Lecture Notes in Computer Science | volume = 6371 | pages = 215–230 | doi = 10.1007/978-3-642-15898-8_14 | isbn = 978-3-642-15897-1 | chapter-url= https://doi.org/10.1007/978-3-642-15898-8_14}}</ref> | ||
* [[नियंत्रण इंजीनियरिंग]]<ref name="DavidAlla2005"/><ref>{{cite journal |last1=Gao |first1=X. |last2=Hu |first2=Xinyan |title=नए पेस्ट बैकफिल प्रोसेस मॉडल के लिए एक पेट्री नेट न्यूरल नेटवर्क मजबूत नियंत्रण|journal=IEEE Access |date=2020 |volume=8 |pages=18420–18425 |doi=10.1109/ACCESS.2020.2968510|s2cid=210994447 |doi-access=free }}</ref><ref>{{Cite journal|last1=Kučera|first1=Erik|last2=Haffner|first2=Oto|last3=Drahoš|first3=Peter|last4=Leskovský|first4=Roman|last5=Cigánek|first5=Ján|date=January 2020|title=PetriNet Editor + PetriNet Engine: New Software Tool For Modelling and Control of Discrete Event Systems Using Petri Nets and Code Generation|journal=Applied Sciences|language=en|volume=10|issue=21|pages=7662|doi=10.3390/app10217662|doi-access=free}}</ref> | * [[नियंत्रण इंजीनियरिंग]]<ref name="DavidAlla2005"/><ref>{{cite journal |last1=Gao |first1=X. |last2=Hu |first2=Xinyan |title=नए पेस्ट बैकफिल प्रोसेस मॉडल के लिए एक पेट्री नेट न्यूरल नेटवर्क मजबूत नियंत्रण|journal=IEEE Access |date=2020 |volume=8 |pages=18420–18425 |doi=10.1109/ACCESS.2020.2968510|s2cid=210994447 |doi-access=free }}</ref><ref>{{Cite journal|last1=Kučera|first1=Erik|last2=Haffner|first2=Oto|last3=Drahoš|first3=Peter|last4=Leskovský|first4=Roman|last5=Cigánek|first5=Ján|date=January 2020|title=PetriNet Editor + PetriNet Engine: New Software Tool For Modelling and Control of Discrete Event Systems Using Petri Nets and Code Generation|journal=Applied Sciences|language=en|volume=10|issue=21|pages=7662|doi=10.3390/app10217662|doi-access=free}}</ref> | ||
* [[डेटा विश्लेषण]]<ref>{{cite book | first1 = W.M.P. | last1 = van der Aalst | title = प्रोसेस माइनिंग - डेटा साइंस इन एक्शन, दूसरा संस्करण| publisher = Springer | url = https://doi.org/10.1007/978-3-662-49851-4 | date=2016 | doi = 10.1007/978-3-662-49851-4 | isbn = 978-3-662-49850-7 | s2cid = 12806779 }}</ref> | * [[डेटा विश्लेषण]]<ref>{{cite book | first1 = W.M.P. | last1 = van der Aalst | title = प्रोसेस माइनिंग - डेटा साइंस इन एक्शन, दूसरा संस्करण| publisher = Springer | url = https://doi.org/10.1007/978-3-662-49851-4 | date=2016 | doi = 10.1007/978-3-662-49851-4 | isbn = 978-3-662-49850-7 | s2cid = 12806779 }}</ref> | ||
* [[ निदान (कृत्रिम बुद्धि) | * [[ निदान (कृत्रिम बुद्धि) | निदान (कृत्रिम बुद्धि)]]<ref>{{cite book | first1 = J. | last1 = Carmona | first2 = B.F. | last2 = van Dongen | first3 = A. | last3 = Solti | first4 = M. | last4 = Weidlich | title = अनुरूपता जाँच - प्रक्रियाओं और मॉडलों से संबंधित| publisher = Springer | url = https://doi.org/10.1007/978-3-319-99414-7 | date=2018 | doi = 10.1007/978-3-319-99414-7 | isbn = 978-3-319-99413-0 | s2cid = 53250018 }}</ref> | ||
* | *डायग्नोसिस (आर्टिफिशियल इंटेलिजेंस)<ref>{{cite conference | ||
|first = J. L. | |first = J. L. | ||
|last = Fernandez |author2=Sanz, R. |author3=Paz, E. |author4=Alonso, C. | |last = Fernandez |author2=Sanz, R. |author3=Paz, E. |author4=Alonso, C. | ||
| Line 256: | Line 234: | ||
|location = Pasadena, CA, USA | |location = Pasadena, CA, USA | ||
|doi = 10.1109/ROBOT.2008.4543394 | |doi = 10.1109/ROBOT.2008.4543394 | ||
|isbn = 978-1-4244-1646-2 }}</ref><ref>{{cite journal |last1=Mendes |first1=J. Marco |last2=Leitão |first2=Paulo |last3=Colombo |first3=Armando W. |last4=Restivo |first4=Francisco |title=सेवा-उन्मुख निर्माण प्रणालियों में प्रक्रिया विवरण और नियंत्रण के लिए उच्च-स्तरीय पेट्री नेट|journal=International Journal of Production Research |year=2012 |volume=50 |issue=6 |pages=1650–1665 |url=https://doi.org/10.1080/00207543.2011.575892 |publisher=Taylor & Francis|doi=10.1080/00207543.2011.575892 |s2cid=39688855 }}</ref><ref>{{cite conference | first1 = D. | last1 = Fahland| first2 = C. | last2 = Gierds| title = Active Flow and Combustion Control 2018| date = 2013 | chapter = Analyzing and Completing Middleware Designs for Enterprise Integration Using Coloured Petri Nets | conference = Advanced Information Systems Engineering - 25th International Conference, CAiSE 2013 | series = Lecture Notes in Computer Science | volume = 7908| pages = 400–416 | doi = 10.1007/978-3-642-38709-8_26| isbn = 978-3-319-98176-5| doi-access = free }}</ref> | |isbn = 978-1-4244-1646-2 }}</ref> | ||
* अनुक्रमिक फ़ंक्शन चार्ट<ref>{{cite journal |last1=Mendes |first1=J. Marco |last2=Leitão |first2=Paulo |last3=Colombo |first3=Armando W. |last4=Restivo |first4=Francisco |title=सेवा-उन्मुख निर्माण प्रणालियों में प्रक्रिया विवरण और नियंत्रण के लिए उच्च-स्तरीय पेट्री नेट|journal=International Journal of Production Research |year=2012 |volume=50 |issue=6 |pages=1650–1665 |url=https://doi.org/10.1080/00207543.2011.575892 |publisher=Taylor & Francis|doi=10.1080/00207543.2011.575892 |s2cid=39688855 }}</ref><ref>{{cite conference | first1 = D. | last1 = Fahland| first2 = C. | last2 = Gierds| title = Active Flow and Combustion Control 2018| date = 2013 | chapter = Analyzing and Completing Middleware Designs for Enterprise Integration Using Coloured Petri Nets | conference = Advanced Information Systems Engineering - 25th International Conference, CAiSE 2013 | series = Lecture Notes in Computer Science | volume = 7908| pages = 400–416 | doi = 10.1007/978-3-642-38709-8_26| isbn = 978-3-319-98176-5| doi-access = free }}</ref> | |||
* [[खेल सिद्धांत]]<ref>{{cite journal |last1=Clempner |first1=Julio |title=Modeling shortest path games with Petri nets: a Lyapunov based theory |journal=International Journal of Applied Mathematics and Computer Science |date=2006 |volume=16 |issue=3 |pages=387–397 |url=http://pldml.icm.edu.pl/pldml/element/bwmeta1.element.bwnjournal-article-amcv16i3p387bwm |language=EN |issn=1641-876X}}</ref> | * [[खेल सिद्धांत]]<ref>{{cite journal |last1=Clempner |first1=Julio |title=Modeling shortest path games with Petri nets: a Lyapunov based theory |journal=International Journal of Applied Mathematics and Computer Science |date=2006 |volume=16 |issue=3 |pages=387–397 |url=http://pldml.icm.edu.pl/pldml/element/bwmeta1.element.bwnjournal-article-amcv16i3p387bwm |language=EN |issn=1641-876X}}</ref> | ||
* [[सिग्नल संक्रमण रेखांकन]]<ref>{{Cite book|date=2000|editor-last=Yakovlev|editor-first=Alex|editor2-last=Gomes|editor2-first=Luis|editor3-last=Lavagno|editor3-first=Luciano|title=हार्डवेयर डिजाइन और पेट्री नेट|url=https://doi.org/10.1007/978-1-4757-3143-9|language=en-gb|doi=10.1007/978-1-4757-3143-9|isbn=978-1-4419-4969-1}}</ref><ref>{{Cite journal|last1=Cortadella|first1=J.|author1-link=Jordi Cortadella|last2=Kishinevsky|first2=M.|last3=Kondratyev|first3=A.|last4=Lavagno|first4=L.|last5=Yakovlev|first5=A.|date=2002|title=अतुल्यकालिक नियंत्रकों और इंटरफेस के लिए तर्क संश्लेषण|url=https://doi.org/10.1007/978-3-642-55989-1|journal=Springer Series in Advanced Microelectronics|volume=8|language=en-gb|doi=10.1007/978-3-642-55989-1|isbn=978-3-642-62776-7|issn=1437-0387}}</ref><ref>{{Cite journal|date=2002|editor-last=Cortadella|editor-first=Jordi|editor1-link=Jordi Cortadella|editor2-last=Yakovlev|editor2-first=Alex|editor3-last=Rozenberg|editor3-first=Grzegorz|title=संगामिति और हार्डवेयर डिजाइन|url=https://doi.org/10.1007/3-540-36190-1|journal=Lecture Notes in Computer Science|volume=2549|language=en-gb|doi=10.1007/3-540-36190-1|isbn=978-3-540-00199-7|s2cid=42026227|issn=0302-9743}}</ref> | * [[सिग्नल संक्रमण रेखांकन]]<ref>{{Cite book|date=2000|editor-last=Yakovlev|editor-first=Alex|editor2-last=Gomes|editor2-first=Luis|editor3-last=Lavagno|editor3-first=Luciano|title=हार्डवेयर डिजाइन और पेट्री नेट|url=https://doi.org/10.1007/978-1-4757-3143-9|language=en-gb|doi=10.1007/978-1-4757-3143-9|isbn=978-1-4419-4969-1}}</ref><ref>{{Cite journal|last1=Cortadella|first1=J.|author1-link=Jordi Cortadella|last2=Kishinevsky|first2=M.|last3=Kondratyev|first3=A.|last4=Lavagno|first4=L.|last5=Yakovlev|first5=A.|date=2002|title=अतुल्यकालिक नियंत्रकों और इंटरफेस के लिए तर्क संश्लेषण|url=https://doi.org/10.1007/978-3-642-55989-1|journal=Springer Series in Advanced Microelectronics|volume=8|language=en-gb|doi=10.1007/978-3-642-55989-1|isbn=978-3-642-62776-7|issn=1437-0387}}</ref><ref>{{Cite journal|date=2002|editor-last=Cortadella|editor-first=Jordi|editor1-link=Jordi Cortadella|editor2-last=Yakovlev|editor2-first=Alex|editor3-last=Rozenberg|editor3-first=Grzegorz|title=संगामिति और हार्डवेयर डिजाइन|url=https://doi.org/10.1007/3-540-36190-1|journal=Lecture Notes in Computer Science|volume=2549|language=en-gb|doi=10.1007/3-540-36190-1|isbn=978-3-540-00199-7|s2cid=42026227|issn=0302-9743}}</ref> | ||
| Line 264: | Line 243: | ||
* [[सिमुलेशन]]<ref name="AalstStahl2011"/>* [[सॉफ्टवेर डिज़ाइन]]<ref name=":0">{{Cite journal|last1=Kučera|first1=Erik|last2=Haffner|first2=Oto|last3=Drahoš|first3=Peter|last4=Cigánek|first4=Ján|last5=Leskovský|first5=Roman|last6=Štefanovič|first6=Juraj|date=January 2020|title=टाइम्ड इंटरप्रिटेड पेट्री नेट्स का उपयोग करके डिस्क्रीट-इवेंट और हाइब्रिड सिस्टम के मॉडलिंग और नियंत्रण के लिए नया सॉफ्टवेयर टूल|journal=Applied Sciences|language=en|volume=10|issue=15|pages=5027|doi=10.3390/app10155027|doi-access=free}}</ref> | * [[सिमुलेशन]]<ref name="AalstStahl2011"/>* [[सॉफ्टवेर डिज़ाइन]]<ref name=":0">{{Cite journal|last1=Kučera|first1=Erik|last2=Haffner|first2=Oto|last3=Drahoš|first3=Peter|last4=Cigánek|first4=Ján|last5=Leskovský|first5=Roman|last6=Štefanovič|first6=Juraj|date=January 2020|title=टाइम्ड इंटरप्रिटेड पेट्री नेट्स का उपयोग करके डिस्क्रीट-इवेंट और हाइब्रिड सिस्टम के मॉडलिंग और नियंत्रण के लिए नया सॉफ्टवेयर टूल|journal=Applied Sciences|language=en|volume=10|issue=15|pages=5027|doi=10.3390/app10155027|doi-access=free}}</ref> | ||
* [[वर्कफ़्लो प्रबंधन प्रणाली]]<ref>{{cite book |last1=ter Hofstede |first1=Arthur H. M. |last2=van der Aalst |first2=Wil M. P. |last3=Adams |first3=Michael |last4=Russell |first4=Nick |editor4-first=Nick |editor4-last=Russell |editor3-first=Michael |editor3-last=Adams |editor2-first=Wil M. P |editor2-last=Aalst |editor1-first=Arthur H. M |editor1-last=Hofstede |title=आधुनिक व्यवसाय प्रक्रिया स्वचालन - YAWL और इसका समर्थन पर्यावरण|url=https://doi.org/10.1007/978-3-642-03121-2 |date=2010|doi=10.1007/978-3-642-03121-2 |isbn=978-3-642-03122-9 }}</ref><ref name="AalstWFpattern2018"/><ref name="AalstWFanalysis2018"/> | * [[वर्कफ़्लो प्रबंधन प्रणाली]]<ref>{{cite book |last1=ter Hofstede |first1=Arthur H. M. |last2=van der Aalst |first2=Wil M. P. |last3=Adams |first3=Michael |last4=Russell |first4=Nick |editor4-first=Nick |editor4-last=Russell |editor3-first=Michael |editor3-last=Adams |editor2-first=Wil M. P |editor2-last=Aalst |editor1-first=Arthur H. M |editor1-last=Hofstede |title=आधुनिक व्यवसाय प्रक्रिया स्वचालन - YAWL और इसका समर्थन पर्यावरण|url=https://doi.org/10.1007/978-3-642-03121-2 |date=2010|doi=10.1007/978-3-642-03121-2 |isbn=978-3-642-03122-9 }}</ref><ref name="AalstWFpattern2018"/><ref name="AalstWFanalysis2018"/> | ||
== यह भी देखें == | == यह भी देखें == | ||
* [[परिमित अवस्था मशीन]] | * [[परिमित अवस्था मशीन]] | ||
| Line 420: | Line 397: | ||
| isbn = 978-981-02-3029-6}} | | isbn = 978-981-02-3029-6}} | ||
{{DEFAULTSORT:Petri Net}} | |||
{{DEFAULTSORT:Petri Net}} | |||
[[Category: | [[Category:CS1 British English-language sources (en-gb)]] | ||
[[Category:Created On 02/03/2023]] | [[Category:CS1 Deutsch-language sources (de)]] | ||
[[Category:CS1 English-language sources (en)]] | |||
[[Category:Created On 02/03/2023|Petri Net]] | |||
[[Category:Lua-based templates|Petri Net]] | |||
[[Category:Machine Translated Page|Petri Net]] | |||
[[Category:Pages with reference errors]] | |||
[[Category:Pages with script errors|Petri Net]] | |||
[[Category:Short description with empty Wikidata description|Petri Net]] | |||
[[Category:Templates Vigyan Ready|Petri Net]] | |||
[[Category:Templates that add a tracking category|Petri Net]] | |||
[[Category:Templates that generate short descriptions|Petri Net]] | |||
[[Category:Templates using TemplateData|Petri Net]] | |||
[[Category:औपचारिक विनिर्देश भाषाएँ|Petri Net]] | |||
[[Category:गणना के मॉडल|Petri Net]] | |||
[[Category:चित्र|Petri Net]] | |||
[[Category:पेट्री डिश|Petri Net]] | |||
[[Category:मॉडलिंग भाषाएँ|Petri Net]] | |||
[[Category:समवर्ती (कंप्यूटर विज्ञान)|Petri Net]] | |||
[[Category:सॉफ्टवेयर मॉडलिंग भाषा|Petri Net]] | |||
Latest revision as of 17:48, 15 March 2023
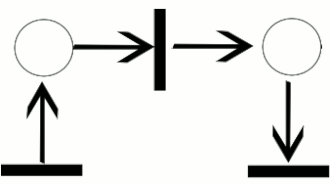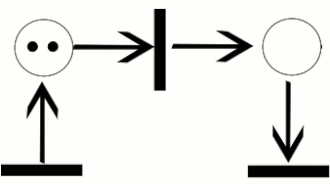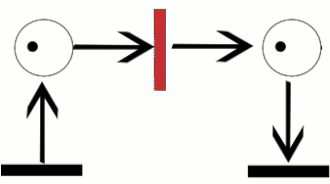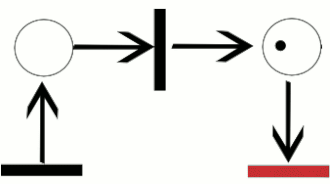
पेट्री नेट, जिसे एक स्थान/संक्रमण (पीटी) नेट के रूप में भी जाना जाता है, वितरित प्रणाली के विवरण के लिए कई गणितीय मॉडलिंग भाषाओं में से एक होता है। यह असतत घटना गतिशील प्रणाली का एक वर्ग है। पेट्री नेट एक निर्देशित द्विपक्षीय ग्राफ है जिसमें दो प्रकार के तत्व, स्थान और संक्रमण होते है। स्थान तत्वों को सफेद घेरे के रूप में दर्शाया गया है और संक्रमण तत्वों को आयतों के रूप में दर्शाया गया है। किसी स्थान में कितने भी टोकन हो सकते है, जिन्हें काले घेरों के रूप में दर्शाया गया है। यदि इनपुट के रूप में इससे जुड़े सभी स्थानों में कम से कम एक टोकन हो तो एक संक्रमण सक्षम हो जाता है। कुछ स्रोत[1] कहते है कि रासायनिक प्रक्रियाओं का वर्णन करने के उद्देश्य से अगस्त 1939 में कार्ल एडम पेट्री द्वारा 13 साल की उम्र में पेट्री नेट का आविष्कार किया गया था।
यूएमएल गतिविधि आरेख, बिजनेस प्रोसेस मॉडल और नोटेशन, और घटना-संचालित प्रक्रिया श्रृंखला जैसे उद्योग मानकों की तरह, पेट्री नेट चरणवार प्रक्रियाओं के लिए ग्राफिकल नोटेशन प्रदान करते है जिसमें पसंद, पुनरावृत्ति और समवर्ती निष्पादन सम्मलित होते है। इन मानकों के विपरीत, पेट्री नेट के पास प्रक्रिया विश्लेषण के लिए एक सुविकसित गणितीय सिद्धांत के साथ उनके निष्पादन शब्दार्थ की एक त्रुटिहीन गणितीय परिभाषा है।
ऐतिहासिक पृष्ठभूमि
जर्मन कंप्यूटर वैज्ञानिक कार्ल एडम पेट्री, जिनके नाम पर इस तरह की संरचनाओं का नाम दिया गया है, उन्होने अपने 1962 के निबंध कॉम्यूनिकेशन मिट ऑटोमेटन में पेट्री नेट का बड़े पैमाने पर विश्लेषण किया था।
पेट्री नेट मूल बातें
पेट्री नेट में स्थान, संक्रमण और ग्राफ सिद्धांत सम्मलित होते है। चाप एक स्थान से संक्रमण या इसके विपरीत चलते है, स्थानों के बीच या संक्रमण के बीच कभी नहीं चलते है। जिन स्थानों से चाप एक संक्रमण तक चलता है उन्हें संक्रमण के इनपुट स्थान कहा जाता है, जिन स्थानों पर संक्रमण से चाप चलते है उन्हें संक्रमण के आउटपुट स्थान कहा जाता है।
ग्राफिक रूप से, पेट्री नेट में स्थानों में असतत संख्या में चिह्न हो सकते है जिन्हें टोकन कहा जाता है। स्थानों पर टोकन का कोई भी वितरण अंकन कहे जाने वाले नेट के विन्यास का प्रतिनिधित्व करता है। पेट्री नेट आरेख से संबंधित एक अमूर्त अर्थ में, पेट्री नेट का एक संक्रमण सक्रिय हो सकता है यदि यह सक्षम है, अर्थात इसके सभी इनपुट स्थानों में पर्याप्त टोकन है, जब संक्रमण प्रारंभ होता है, तो यह आवश्यक इनपुट टोकन का उपभोग करता है, और इसके आउटपुट स्थानों में टोकन बनाता है।
जब तक एक निष्पादन नीति (उदाहरण के लिए संक्रमणों का एक सख्त क्रम, पूर्वता का वर्णन) परिभाषित नहीं किया जाता है, पेट्री नेट का निष्पादन गैर-नियतात्मक होता है: जब एक ही समय में कई संक्रमण सक्षम होते है, तो वे किसी भी क्रम में सक्रिय हो जाते है।
चूंकि फायरिंग गैर-नियतात्मक है, और कई टोकन नेट में कहीं भी उपस्तिथ हो सकते है (यहां तक कि एक ही स्थान पर), पेट्री नेट वितरित प्रणाली के समवर्ती व्यवहार के मॉडलिंग के लिए उपयुक्त होती है।
औपचारिक परिभाषा और बुनियादी शब्दावली
पेट्री नेट राज्य संक्रमण प्रणाली है जो प्राथमिक नेट नामक नेटों के एक वर्ग का विस्तार करती है।[2]
परिभाषा 1. 'नेट' एक टपल है जहां
- और क्रमशः स्थानों और संक्रमणों के असंयुक्त परिमित समुच्चय है।
- (निर्देशित) चापों (या प्रवाह संबंधों) का एक सेट है।
'परिभाषा 2.' नेट एन = (पी, टी, एफ) दिया गया है, विन्यास एक सेट सी है जिससे कि सी <बड़ा>⊆</बड़ा> पी है।
परिभाषा 3. एक प्रारंभिक नेट EN = (N, C) रूप का नेट है जहां
- N = (P, T, F) एक नेट है।
- 'सी' ऐसा है कि सी <बड़ा>⊆</बड़ा> पी एक विन्यास है।
परिभाषा 4. पेट्री नेट पीएन = (एन, एम, डब्ल्यू) के रूप का नेट है, जो प्राथमिक नेट का विस्तार करता है जिससे कि
- N = (P, T, F) एक नेट है।
- M : P → Z एक जगह मल्टीसेट है, जहां Z एक गणनीय सेट है। एम विन्यास की अवधारणा का विस्तार करता है और इसे सामान्यतः पेट्री नेट डायग्राम के संदर्भ में मार्किंग के रूप में वर्णित किया जाता है।
- W : F → Z एक चाप मल्टीसेट है, जिससे कि प्रत्येक चाप के लिए गिनती (या वजन) चाप की बहुलता का माप किया जाता है।
यदि पेट्री नेट एक प्राथमिक नेट के बराबर है, तो Z काउंटेबल सेट {0,1} हो सकता है और P में वे तत्व जो M के अनुसार 1 को मैप करते है, एक विन्यास बनाते है। इसी तरह, यदि पेट्री नेट प्राथमिक नेट नहीं है, तो मल्टीसेट M की व्याख्या विन्यास के गैर-सिंगलटन सेट का प्रतिनिधित्व करने के रूप में की जा सकती है। इस संबंध में, 'एम' पेट्री नेट के लिए प्रारंभिक नेट के लिए विन्यास की अवधारणा का विस्तार करता है।
पेट्री नेट के आरेख में, स्थानों को पारंपरिक रूप से मंडलियों के साथ चित्रित किया गया है, लंबे संकीर्ण आयतों के साथ संक्रमण और एक तरफा तीर के रूप में चाप जो स्थानों के संक्रमण या संक्रमण के स्थानों के कनेक्शन दिखाते है। यदि आरेख एक प्राथमिक नेट का होता है, तो विन्यास में उन स्थानों को पारंपरिक रूप से मंडलियों के रूप में दर्शाया जाता है, जहां प्रत्येक वृत्त में एक बिंदु सम्मलित होता है जिसे टोकन कहा जाता है। पेट्री नेट के दिए गए आरेख में, स्थान चक्रों में एक से अधिक टोकन सम्मलित हो सकते है, यह दिखाने के लिए कि विन्यास में कोई स्थान कितनी बार दिखाई देता है। संपूर्ण पेट्री नेट आरेख पर वितरित टोकन के विन्यास को अंकन कहा जाता है।
शीर्ष आकृति में (दाएं देखें), स्थान p1 संक्रमण t का एक इनपुट स्थान है, जबकि, स्थान p2 उसी संक्रमण के लिए एक आउटपुट स्थान है। बता दें कि PN0 (ऊपरी आकृति) कॉन्फ़िगर किए गए M0 के साथ पेट्री नेट है, और PN1 (नीचे का आंकड़ा) कॉन्फ़िगर किए गए M1 के साथ पेट्री नेट है। PN0 का विन्यास संपत्ति के माध्यम से संक्रमण टी को सक्षम करता है कि सभी इनपुट स्थानों में टोकन की पर्याप्त संख्या होती है। केवल एक बार संक्रमण सक्षम हो जाने पर संक्रमण सक्रिय हो जाता है। इस उदाहरण में, संक्रमण टी की फायरिंग एक नक्शा उत्पन्न करती है जिसमें M0 की छवि में मार्किंग कॉन्फ़िगर किया गया M1 होता है और पेट्री नेट PN1 में परिणाम होता है, जो नीचे की आकृति में देखा जाता है। आरेख में, एक संक्रमण के लिए फायरिंग नियम को इसके इनपुट स्थानों से संबंधित इनपुट चाप्स की बहुलता के बराबर कई टोकन घटाकर और संबंधित की बहुलता के बराबर आउटपुट स्थानों पर टोकन की एक नई संख्या जमा करके चित्रित किया जा सकता है।
टिप्पणी 1. "बराबर या अधिक" का त्रुटिहीन अर्थ फायरिंग नियम में Z पर लागू होने वाले जोड़ के त्रुटिहीन बीजगणितीय गुणों पर निर्भर करेगा, जहां बीजगणितीय गुणों पर सूक्ष्म भिन्नताएं पेट्री नेट के अन्य वर्गों को जन्म दे सकती है, उदाहरण के लिए, बीजगणितीय पेट्री नेट।[3]
निम्नलिखित औपचारिक परिभाषा शिथिल रूप से (पीटरसन 1981) पर आधारित है। कई वैकल्पिक परिभाषाएँ उपस्तिथ है।
वाक्य - विन्यास
पेट्री नेट ग्राफ (कुछ लोगों द्वारा पेट्री नेट कहा जाता है, लेकिन नीचे देखें) एक 3-टपल है , जहाँ
- S स्थानों का परिमित समुच्चय है
- T संक्रमणों का परिमित समुच्चय है
- S और T असंयुक्त समुच्चय है, अर्थात कोई भी वस्तु स्थान और संक्रमण दोनों नहीं हो सकती
- निर्देशित किनारों का एक मल्टीसेट है, अर्थात यह प्रत्येक चाप को एक गैर-नकारात्मक पूर्णांक चाप बहुलता (या वजन) प्रदान करता है, ध्यान दें कि कोई चाप दो स्थानों या दो संक्रमणों को नहीं जोड़ सकता है।
प्रवाह संबंध चापों का समुच्चय है: . कई पाठ्यपुस्तकों में, चापों में केवल बहुलता हो सकती है। ये पाठ अधिकांशतः W के अतिरिक्त F का उपयोग करके पेट्री नेट को परिभाषित करते है। इस सम्मेलन का उपयोग करते समय, पेट्री नेट ग्राफ एक द्विदलीय ग्राफ मल्टीग्राफ होता है। नोड विभाजन एस और टी के साथ होता है।
संक्रमण t का प्रीसेट इसके इनपुट स्थानों का सेट है: ;
इसका पोस्टसेट इसके आउटपुट स्थानों का सेट है: . स्थानों के पूर्व और बाद के सेट की परिभाषाएं समान है।
पेट्री नेट (ग्राफ) का एक अंकन इसके स्थानों का एक मल्टीसेट है, अर्थात मैपिंग . हम कहते है कि अंकन प्रत्येक स्थान को कई टोकन प्रदान करता है।
एक 'पेट्री नेट' (कुछ लोगों द्वारा चिह्नित पेट्री नेट कहा जाता है, ऊपर देखें) एक 4-ट्यूपल है , जहाँ
- पेट्री नेट ग्राफ है,
- प्रारंभिक अंकन है, पेट्री नेट ग्राफ का अंकन है।
निष्पादन शब्दार्थ
शब्दों में
- एक संक्रमण फायरिंग t अंकन में M खपत करता है इसके प्रत्येक इनपुट स्थान से टोकन s, और उत्पन्न करता है इसके प्रत्येक आउटपुट स्थानों में टोकन s
- एक संक्रमण सक्षम है (यह आग लग सकता है) में M यदि इसके इनपुट स्थान में पर्याप्त टोकन है तो उपभोग संभव हो सकता है, अर्थात यदि और केवल यदि .
हम सामान्यतः इस बात में रुचि रखते है कि क्या हो सकता है जब संक्रमण मनमाने क्रम में लगातार आग लगा सकता है।
हम कहते है कि एक अंकन M' अंकन से पहुंचा जा सकता है M यदि एक चरण में , हम कहते है कि यह से पहुंच योग्य है M यदि , जहाँ का स्वतुल्य सकर्मक संवरण है ; अर्थात, यदि यह 0 या अधिक चरणों में पहुंचा जा सकता है।
एक (चिह्नित) पेट्री नेट के लिए , हम उन फायरिंग में रुचि रखते है जिन्हें प्रारंभिक मार्किंग से प्रारंभ किया जा सकता है . इसके पहुंच योग्य चिह्नों का सेट है पहुंच योग्यता ग्राफ N संक्रमण संबंध है इसके पहुंच योग्य चिह्नों तक ही सीमित है . यह नेट का राज्य अंतरिक्ष है।
ग्राफ के साथ पेट्री नेट के लिए फायरिंग सीक्वेंस G और प्रारंभिक अंकन संक्रमणों का क्रम है ऐसा है कि . फायरिंग सीक्वेंस के सेट को इस रूप में दर्शाया गया है .
परिभाषा पर बदलाव
चाप बहुलता को अस्वीकार करने और चाप डब्ल्यू के बैग को एक साधारण सेट के साथ बदलने के लिए एक सामान्य भिन्नता है, जिसे प्रवाह संबंध कहा जाता है, .
यह अभिव्यंजक शक्ति (कंप्यूटर विज्ञान) को सीमित नहीं करता है क्योंकि दोनों एक दूसरे का प्रतिनिधित्व कर सकते है।
देसेल और जुहास (2001) में,[4] क्षमता को स्थानों पर परिभाषित करने की अनुमति दिया था। इस पर नीचे विस्तार के अनुसार चर्चा की गई है।
सदिशों और आव्यूहों के संदर्भ में निरूपण
पेट्री नेट के निशान लंबाई के गैर-नकारात्मक पूर्णांकों के वेक्टर (गणित) के रूप में माना जा सकता है .
इसके संक्रमण संबंध को एक जोड़ी के रूप में वर्णित किया जा सकता है द्वारा मैट्रिक्स (गणित):
- , द्वारा परिभाषित
- , द्वारा परिभाषित
फिर उनका अंतर
मैट्रिक्स गुणा के संदर्भ में पहुंच योग्य चिह्नों का वर्णन करने के लिए निम्नानुसार उपयोग किया जा सकता है।
संक्रमण के किसी भी क्रम के लिए w, लिखना वेक्टर के लिए जो प्रत्येक संक्रमण को इसकी घटनाओं की संख्या में मैप करता है w. तो हमारे पास है
- .
यह आवश्यक होना चाहिए w फायरिंग सीक्वेंस है, संक्रमणों के मनमाना अनुक्रमों की अनुमति देना सामान्यतः एक बड़ा सेट उत्पन्न करता है।
श्रेणी-सैद्धांतिक सूत्रीकरण
मेसेगुएर और मोंटानारी को एक प्रकार की सममित मोनोइडल श्रेणियां माना जाता है जिन्हें पेट्री श्रेणियों के रूप में जाना जाता है।[5]
पेट्री नेट के गणितीय गुण
पेट्री नेट को रोचक बनाने वाली एक बात यह है कि वे मॉडलिंग शक्ति और विश्लेषण क्षमता के बीच संतुलन प्रदान करते है: पेट्री नेट के लिए समवर्ती प्रणालियों के बारे में बहुत सी चीजें स्वचालित रूप से निर्धारित की जा सकती है, चूंकि उनमें से कुछ चीजें सामान्य रूप से निर्धारित करने के लिए बहुत महंगी होती है। पेट्री नेट के कई उपवर्गों का अध्ययन किया गया है जो अभी भी समवर्ती प्रणालियों के रोचक वर्गों का मॉडल बना सकते है, जबकि ये समस्याएं आसान हो जाती है।
पेट्री नेट और कुछ उपवर्गों के लिए निर्णायकता और जटिलता परिणामों के साथ इस तरह की निर्णय समस्याओं का अवलोकन एस्पार्ज़ा और नीलसन (1995) में पाया जा सकता है।[6]
गम्यता
पेट्री नेट के लिए रीचबिलिटी की समस्या यह तय करना है कि पेट्री नेट एन और मार्किंग एम दिया गया है या नहीं .
यह ऊपर परिभाषित गम्यता-ग्राफ चलने की स्थिति है, जब तक या अनुरोधित-अंकन नहीं हो जाता है या अब नहीं मिल सकता है। यह पहले की तुलना में कठिन है: गम्यता ग्राफ सामान्यतः अनंत है, और यह निर्धारित करना आसान नहीं है कि कब रुकना सुरक्षित है।
वास्तव में, इस समस्या को एक्सपस्पेस-कठिन दिखाया गया था[7] सालों पहले इसे बिल्कुल भी निर्णायक दिखाया गया था (मेयर, 1981)। इसे कुशलतापूर्वक कैसे किया जाए, इस पर शोध पत्र प्रकाशित होते रहते है।[8] 2018 में, ज़ेरविंस्की एट अल ने निचली सीमा में सुधार किया और दिखाया कि समस्या प्राथमिक नहीं है।[9] 2021 में, जेरोम लेरोक्स द्वारा स्वतंत्र रूप से इस समस्या को गैर-आदिम पुनरावर्ती दिखाया गया था[10] और वोज्शिएक ज़ेरविन्स्की और लुकाज़ ऑरलिकोव्स्की द्वारा दिखाया गया था।[11] इस प्रकार ये परिणाम लंबे समय से चली आ रही जटिलता को बंद कर देते है।
जबकि गम्यता गलत राज्यों को खोजने के लिए एक अच्छा उपकरण प्रतीत होता है, व्यावहारिक समस्याओं के लिए निर्मित ग्राफ में सामान्यतः गणना करने के लिए बहुत अधिक राज्य होते है। इस समस्या को कम करने के लिए, रैखिक लौकिक तर्क का उपयोग सामान्यतः यह सिद्ध करने के लिए विश्लेषणात्मक विधि के संयोजन में किया जाता है कि ऐसी अवस्थाओं तक नहीं पहुँचा जा सकता है। रैखिक लौकिक तर्क अर्ध-निर्णय प्रक्रिया तकनीक का उपयोग यह पता लगाने के लिए करता है कि क्या वास्तव में एक राज्य तक पहुँचा जा सकता है, राज्य तक पहुँचने के लिए आवश्यक शर्तों का एक सेट खोज कर, यह सिद्ध करते हुए कि उन शर्तों को संतुष्ट नहीं किया जा सकता है।
सजीवता
पेट्री नेट को जीवंतता की विभिन्न डिग्री के रूप में वर्णित किया जा सकता है . वह पेट्री नेट कहा जाता है -जीएं और केवल यदि इसके सभी संक्रमण है -लाइव, जहां एक संक्रमण है
- मृत, यदि यह कभी भी फायर नहीं कर सकता है, अर्थात यह फायरिंग सीक्वेंस में नहीं है
- -लाइव (संभावित रूप से फायर करने योग्य), यदि और केवल यदि यह फायर कर सकता है, अर्थात यह कुछ फायरिंग सीक्वेंस में है
- -Live यदि यह मनमाने ढंग से अधिकांशतः आग लगा सकता है, अर्थात यदि हर सकारात्मक पूर्णांक के लिए k, यह कम से कम होता है k बार कुछ फायरिंग सीक्वेंस में है
- -लाइव यदि यह असीम रूप से अधिकांशतः आग लगा सकता है, अर्थात यदि कुछ निश्चित (आवश्यक अनंत) फायरिंग अनुक्रम है जिसमें प्रत्येक सकारात्मक पूर्णांक के लिए k, संक्रमण कम से कम होता है k,
- -लाइव (लाइव) यदि यह हमेशा आग लगा सकता है, अर्थात यह है में हर पहुंच योग्य अंकन में रहते है
ध्यान दें कि ये तेजी से कठोर आवश्यकताएं है: -जीवंतता का तात्पर्य है -जीवंतता, के लिए है .
ये परिभाषाएँ मुराता के अवलोकन के अनुसार है,[12] जो अतिरिक्त रूप से उपयोग करता है -मृत के लिए एक शब्द के रूप में जीना होता है।
सीमाबद्धता
पेट्री नेट में एक जगह को के-बाउंड कहा जाता है यदि इसमें प्रारंभिक अंकन सहित सभी पहुंच योग्य चिह्नों में के टोकन से अधिक नहीं होते है, यदि यह 1-बाध्य है तो इसे सुरक्षित कहा जाता है, यह परिबद्ध है यदि यह कुछ k के लिए k-बाध्य है।
ए (चिन्हित) पेट्री नेट को के-बाउंडेड, सेफ या बाउंडेड कहा जाता है जब इसके सभी स्थान होते है। पेट्री नेट (ग्राफ) को (संरचनात्मक रूप से) बाउंडेड कहा जाता है यदि यह हर संभव प्रारंभिक अंकन के लिए बाउंड होता है।
पेट्री नेट बंधा हुआ है केवल यदि इसकी गम्यता ग्राफ परिमित होता है।
रिचर्ड कार्प-मिलर ट्री का निर्माण करके, कवरिंग समस्या को देखते हुए बाउंडेडनेस निर्णायक होता है।
किसी दिए गए नेट में स्थानों पर स्पष्ट रूप से बाध्य होना उपयोगी हो सकता है। इसका उपयोग सीमित प्रणाली संसाधनों को मॉडल करने के लिए किया जा सकता है।
पेट्री नेट की कुछ परिभाषाएँ स्पष्ट रूप से इसे एक वाक्यगत विशेषता के रूप में अनुमति देता है।[13] औपचारिक रूप से, स्थान क्षमता वाले पेट्री नेट को टुपल्स के रूप में परिभाषित किया जा सकता है , कहाँ पेट्री नेट है, (कुछ या सभी) स्थानों के लिए क्षमताओं का एक असाइनमेंट, और संक्रमण संबंध सामान्य रूप से चिह्नों तक सीमित होता है जिसमें क्षमता वाले प्रत्येक स्थान पर अधिक से अधिक कई टोकन होते है।
उदाहरण के लिए, यदि नेट N में, दोनों स्थानों को क्षमता 2 निर्दिष्ट की गई है, तो हम स्थान क्षमताओं के साथ पेट्री नेट प्राप्त करते है, N2 कहते है, इसका गम्यता ग्राफ दाईं ओर प्रदर्शित होती है।
वैकल्पिक रूप से, नेट को फैलाकर स्थानों को घेरा जा सकता है। त्रुटिहीन होने के लिए, स्थान के विपरीत प्रवाह के साथ "काउंटर-प्लेस" जोड़कर और दोनों स्थानों में कुल बनाने के लिए टोकन जोड़कर एक जगह को के-बाध्य बनाया जा सकता है।
असतत, निरंतर और संकर पेट्री नेट
साथ ही असतत घटनाओं के लिए, निरंतर और संकर असतत-निरंतर प्रक्रियाओं के लिए पेट्री नेट होता है[14]जो असतत, सतत और संकर नियंत्रण सिद्धांत में उपयोगी होते है,[15] और असतत, निरंतर और संकर ऑटोमेटा सिद्धांत से संबंधित होते है।
एक्सटेंशन
पेट्री नेट्स के कई विस्तार है। उनमें से कुछ मूल पेट्री नेट के साथ पूरी तरह से पीछे की ओर-संगत (जैसे रंगीन पेट्री नेट) है, कुछ ऐसे गुण जोड़ते है जिन्हें मूल पेट्री नेट औपचारिकता (जैसे समयबद्ध पेट्री नेट) में मॉडल नहीं किया जा सकता है। चूंकि पश्च-संगत मॉडल पेट्री नेट की कम्प्यूटेशनल शक्ति का विस्तार नहीं करते है, उनके पास अधिक संक्षिप्त प्रतिनिधित्व हो सकते है और मॉडलिंग के लिए अधिक सुविधाजनक हो सकते है।[16] एक्सटेंशन जिन्हें पेट्री नेट में परिवर्तित नहीं किया जा सकता है, कभी-कभी बहुत शक्तिशाली होते है, लेकिन सामान्यतः सामान्य पेट्री नेट का विश्लेषण करने के लिए उपलब्ध गणितीय उपकरणों की पूरी श्रृंखला का अभाव होता है।
उच्च स्तरीय पेट्री नेट शब्द का प्रयोग कई पेट्री नेट औपचारिकताओं के लिए किया जाता है जो बुनियादी पी/टी नेट औपचारिकता का विस्तार करते है, इसमें रंगीन पेट्री नेट, पदानुक्रमित पेट्री नेट जैसे नेट के भीतर नेट, और इस खंड में स्केच किए गए अन्य सभी विस्तार सम्मलित होते है। इस शब्द का प्रयोग विशेष रूप से सीपीएन उपकरण द्वारा समर्थित रंगीन नेटों के प्रकार के लिए भी किया जाता है।
संभावित एक्सटेंशन की एक छोटी सूची इस प्रकार है:
- अतिरिक्त प्रकार के चाप, दो सामान्य प्रकार है
- एक रीसेट चाप फायरिंग पर कोई पूर्व शर्त नहीं लगाता है, और संक्रमण के प्रारंभ होने पर जगह को खाली कर देता है, यह पहुंच योग्यता को अनिर्णीत बनाता है,[17] जबकि कुछ अन्य गुण, जैसे समाप्ति, निर्णायक बने रहते है।[18]
- एक अवरोधक चाप पूर्व शर्त लगाता है कि स्थान खाली होने पर ही संक्रमण प्रारंभ हो सकता है, यह व्यक्त किए जाने वाले टोकन की संख्या पर मनमाने ढंग से संगणना की अनुमति देता है, जो औपचारिकता ट्यूरिंग पूर्ण पूर्ण बनाता है और एक सार्वभौमिक नेट के अस्तित्व को दर्शाता है।[19]
- एक मानक पेट्री नेट में, टोकन अप्रभेद्य है। रंगीन पेट्री नेट में, प्रत्येक टोकन का मूल्य होता है।[20] सीपीएन उपकरण्स जैसे रंगीन पेट्री नेट के लिए लोकप्रिय उपकरण में, टोकन के मूल्यों को टाइप किया जाता है, और इसका परीक्षण किया जा सकता है (गार्ड एक्सप्रेशंस का उपयोग करके) और एक कार्यात्मक प्रोग्रामिंग भाषा के साथ हेरफेर किया जा सकता है। रंगीन पेट्री नेटों की एक सहायक पेट्री नेट अच्छी तरह से बनाई गई है, जहां नेट का विश्लेषण करना आसान बनाने के लिए चाप और गार्ड अभिव्यक्ति प्रतिबंधित है।
- पेट्री नेट का एक अन्य लोकप्रिय विस्तार पदानुक्रम है, फेहलिंग द्वारा शोधन और अमूर्तता के समर्थन स्तरों के विभिन्न विचारों के रूप में इसका अध्ययन किया गया था। पदानुक्रम का एक अन्य रूप तथाकथित ऑब्जेक्ट पेट्री नेट या ऑब्जेक्ट प्रणाली में पाया जाता है जहां पेट्री नेट में पेट्री नेट हो सकते है क्योंकि इसके टोकन नेस्टेड पेट्री नेट के पदानुक्रम को प्रेरित करते है जो विभिन्न स्तरों पर संक्रमणों के सिंक्रनाइज़ेशन द्वारा संचार करते है।[21]
- राज्यों (वीएएसएस) के साथ एक वेक्टर जोड़ प्रणाली पेट्री नेट के समान औपचारिकता है। चूँकि, इसे सतही तौर पर पेट्री नेट के सामान्यीकरण के रूप में देखा जा सकता है। एक परिमित राज्य ऑटोमेटन पर विचार करें जहां प्रत्येक संक्रमण को पेट्री नेट से संक्रमण द्वारा लेबल किया जाता है। पेट्री नेट को तब परिमित राज्य ऑटोमेटन के साथ सिंक्रनाइज़ किया जाता है, अर्थात, ऑटोमेटन में एक संक्रमण उसी समय लिया जाता है जब पेट्री नेट में संबंधित संक्रमण होता है। पेट्री नेट में संबंधित संक्रमण सक्षम होने पर ही ऑटोमेटन में एक संक्रमण लेना संभव होता है, और पेट्री नेट में एक संक्रमण को आग लगाना केवल तभी संभव है जब इसके द्वारा लेबल किए गए ऑटोमेटन में वर्तमान स्थिति से कोई संक्रमण होता है। (वीएएसएस की परिभाषा सामान्यतः थोड़ी अलग तरीके से तैयार की जाती है।)
- प्राथमिकता वाले पेट्री नेट संक्रमणों में प्राथमिकताएं जोड़ते है, जिससे एक उच्च-प्राथमिकता संक्रमण सक्षम होने पर एक संक्रमण प्रारंभ नहीं हो सकता है (अर्थात आग लगा सकता है)। इस प्रकार, संक्रमण प्राथमिकता समूहों में है, और प्राथमिकता समूह 3 केवल तब सक्रिय हो सकता है जब समूह 1 और 2 में सभी संक्रमण अक्षम होते है। प्राथमिकता समूह के भीतर, फायरिंग अभी भी गैर-निर्धारिती है।
- गैर-नियतात्मक संपत्ति एक बहुत ही मूल्यवान संपत्ति रही है, क्योंकि यह उपयोगकर्ता को बड़ी संख्या में गुणों को सार करने देती है। चूंकि, कुछ स्थितियों में, केवल एक मॉडल की संरचना ही नहीं, जबकि समय को भी मॉडल करने की आवश्यकता होती है। इन स्थितियों के लिए, समयबद्ध पेट्री नेट विकसित हुए है, जहां ऐसे संक्रमण है जो समयबद्ध है, और संभवतः संक्रमण जो समयबद्ध नहीं है (यदि है, तो समयबद्ध संक्रमणों की समयबद्धता की तुलना में उच्च प्राथमिकता है)। समयबद्ध पेट्री नेट की एक सहायक स्टोकेस्टिक पेट्री नेट है जो संक्रमणों की समायोज्य यादृच्छिकता के माध्यम से गैर-नियतात्मक समय जोड़ता है। घातीय यादृच्छिक वितरण का उपयोग सामान्यतः इन नेटों को 'समय' करने के लिए किया जाता है। इस स्थिति में, नेट गम्यता ग्राफ का उपयोग निरंतर समय मार्कोव श्रृंखला (सीटीएमसी) के रूप में किया जा सकता है।
- द्वैतवादी पेट्री नेट (डीपी-नेट) ई. डाविस, एट अल द्वारा विकसित पेट्री नेट एक्सटेंशन है।[22] वास्तविक दुनिया की प्रक्रिया का बेहतर प्रतिनिधित्व करने के लिए होती है। डीपी-नेट परिवर्तन/अपरिवर्तन, क्रिया/निष्क्रियता, (परिवर्तन) समय/स्थान आदि के द्वंद्व को संतुलित करते है, परिवर्तन और स्थान के द्विदलीय पेट्री नेट निर्माणों के बीच, जिसके परिणामस्वरूप परिवर्तन अंकन की अनूठी विशेषता होती है, अर्थात, जब परिवर्तन काम कर रहा है यह चिह्नित होता है। यह प्रक्रिया थ्रूपुट के वास्तविक दुनिया के व्यवहार का प्रतिनिधित्व करते हुए कई बार आग (या चिह्नित) के परिवर्तन की अनुमति देता है। परिवर्तन का अंकन मानता है कि परिवर्तन का समय शून्य से अधिक होना चाहिए। कई विशिष्ट पेट्री नेट में उपयोग किया जाने वाला शून्य परिवर्तन समय गणितीय रूप से आकर्षक हो सकता है लेकिन वास्तविक दुनिया की प्रक्रियाओं का प्रतिनिधित्व करने में अव्यावहारिक होता है । डीपी-नेट प्रक्रिया संरचना को चित्रित करने के लिए पेट्री नेट्स के पदानुक्रमित अमूर्तता की शक्ति का भी उपयोग करता है। जटिल प्रक्रिया प्रणालियों को पदानुक्रमित अमूर्तता के विभिन्न स्तरों के माध्यम से परस्पर जुड़े सरल नेटों की एक श्रृंखला के रूप में तैयार किया जाता है। एक पैकेट स्विच के प्रक्रिया वास्तुकला को प्रदर्शित किया जाता है,[23] जहां डिजाइन प्रणाली की संरचना के आसपास विकास आवश्यकताओं का आयोजन किया जाता है।
पेट्री नेट के कई और विस्तार है, चूंकि, यह ध्यान रखना महत्वपूर्ण है कि जैसे-जैसे विस्तारित गुणों के संदर्भ में नेट की जटिलता बढ़ती है, नेट के कुछ गुणों का मूल्यांकन करने के लिए मानक उपकरणों का उपयोग करना उतना ही कठिन होता है। इस कारण से, किसी दिए गए मॉडलिंग कार्य के लिए सबसे सरल नेट प्रकार का उपयोग करना एक अच्छा विचार होता है।
प्रतिबंध
पेट्री नेट औपचारिकता को विस्तारित करने के अतिरिक्त, हम इसे प्रतिबंधित करने पर भी देख सकते है, और विशेष प्रकार के पेट्री नेट को देख सकते है, जो एक विशेष तरीके से सिंटैक्स को प्रतिबंधित करके प्राप्त किया जाता है। साधारण पेट्री नेट वे नेट होते है जहां सभी चाप भार 1 होते है। आगे प्रतिबंधित करते हुए, निम्नलिखित प्रकार के साधारण पेट्री नेटों का सामान्यतः उपयोग और अध्ययन किया जाता है:
- एक राज्य मशीन (एसएम) में, प्रत्येक संक्रमण में एक आने वाली चाप और एक बाहर जाने वाली चाप होती है, और सभी चिह्नों में बिल्कुल एक टोकन होता है। परिणाम स्वरुप, समवर्ती नहीं हो सकता है, लेकिन संघर्ष हो सकता है (अर्थात समवर्ती गणना में अनिश्चितता): गणितीय रूप से,
- एक चिह्नित ग्राफ (एमजी) में, प्रत्येक स्थान में एक आने वाली चाप और एक बाहर जाने वाली चाप होती है। इसका अर्थ यह है कि विरोध नहीं हो सकता, लेकिन समवर्ती हो सकता है: गणितीय रूप से,
- फ्री चॉइस नेट (एफसी) में, एक स्थान से एक संक्रमण के लिए प्रत्येक चाप या तो उस स्थान से एकमात्र चाप है या उस संक्रमण के लिए एकमात्र चाप होती है, अर्थात संगामिति और संघर्ष दोनों हो सकते है, लेकिन एक ही समय में नहीं हो सकते है: गणितीय रूप से,
- एक्सटेंडेड फ्री चॉइस (ईएफसी) - पेट्री नेट जिसे एफसी में बदला जा सकता है।
- एक असममित विकल्प नेट (एसी) में, संगामिति और संघर्ष हो सकता है, लेकिन सममित रूप से नहीं हो सकता है: गणितीय रूप से,
कार्यप्रवाह नेट
वर्कफ़्लो नेट (डब्ल्यूएफ-नेट) पेट्री नेट का एक उपवर्ग है जो प्रक्रिया गतिविधियों के वर्कफ़्लो को मॉडल करने का इरादा रखता है।[24] डब्ल्यूएफ-नेट संक्रमण कार्यों या गतिविधियों को सौंपा गया है, और स्थान पूर्व/पोस्ट स्थितियों को असाइन किए गए है। डब्ल्यूएफ-नेट की अतिरिक्त संरचनात्मक और परिचालन आवश्यकताएं होती है, मुख्य रूप से एक एकल इनपुट (स्रोत) स्थान के अतिरिक्त कोई पिछला संक्रमण नहीं है, और आउटपुट स्थान (सिंक) बिना किसी संक्रमण के होता है। तदनुसार, प्रारंभ और समाप्ति चिह्नों को परिभाषित किया जा सकता है जो प्रक्रिया की स्थिति का प्रतिनिधित्व करते है।
डब्ल्यूएफ-नेट में ध्वनि प्रॉपर्टी है,[24] यह दर्शाता है कि अपने स्रोत स्थान पर k टोकन के स्टार्ट मार्किंग के साथ एक प्रक्रिया, अपने सिंक स्थान में k टोकन के साथ समापन स्टेट मार्किंग तक पहुँच सकती है (k- ध्वनि डब्ल्यूएफ-नेट के रूप में परिभाषित) इसके अतिरिक्त, प्रक्रिया में सभी संक्रमण लग सकते है (अर्थात, प्रत्येक संक्रमण के लिए एक पहुंच योग्य स्थिति होती है जिसमें संक्रमण सक्षम होता है)। एक सामान्य ध्वनि (जी-ध्वनि) डब्ल्यूएफ-नेट को प्रत्येक के> 0 के लिए के-ध्वनि के रूप में परिभाषित किया गया है।[25]
पेट्री नेट में एक निर्देशित पथ (ग्राफ सिद्धांत) को निर्देशित चापों से जुड़े नोड्स (स्थानों और संक्रमण) के अनुक्रम के रूप में परिभाषित किया गया है। प्राथमिक पथ में अनुक्रम में प्रत्येक नोड केवल एक बार सम्मलित होता है।
एक अच्छी तरह से नियंत्रित पेट्री नेट एक ऐसा नेट है जिसमें एक स्थान और एक संक्रमण (या संक्रमण और एक स्थान) के बीच पूरी तरह से अलग प्राथमिक पथ नहीं होते है, अर्थात, यदि नोड्स की जोड़ी के बीच दो पथ है तो ये पथ एक नोड साझा करते है। एक विश्वकोश अच्छी तरह से नियंत्रित डब्ल्यूएफ-नेट ध्वनि (जी-ध्वनि) होती है।[26]
विस्तारित डब्ल्यूएफ-नेट पेट्री नेट है जो अतिरिक्त संक्रमण टी (फीडबैक संक्रमण) के साथ डब्ल्यूएफ-नेट से बना होता है। सिंक स्थान संक्रमण टी के इनपुट स्थान और स्रोत स्थान के रूप में इसके आउटपुट स्थान के रूप में जुड़ा हुआ होता है। संक्रमण की फायरिंग प्रक्रिया की पुनरावृत्ति का कारण बनती है।[24]
डब्ल्यूआरआई डब्ल्यूएफ-नेट, एक विस्तारित एसाइक्लिक अच्छी तरह से हैंडल किया जाने वाला डब्ल्यूएफ-नेट है। डब्ल्यूआरआई-डब्ल्यूएफ-नेट को नेट की संरचना के रूप में बनाया जा सकता है, अर्थात, डब्ल्यूआरआई-डब्ल्यूएफ-नेट के भीतर एक सबनेट के साथ एक संक्रमण को बदलना होता है जो डब्ल्यूआरआई-डब्ल्यूएफ-नेट होता है। नतीजा डब्ल्यूआरआई-डब्ल्यूएफ-net भी होता है। डब्ल्यूआरआई-डब्ल्यूएफ-नेट जी-ध्वनि होती है,[26] इसलिए केवल डब्ल्यूआरआई-डब्ल्यूएफ-नेट बिल्डिंग ब्लॉक्स का उपयोग करके, डब्ल्यूएफ-नेट प्राप्त कर सकते है जो निर्माण द्वारा जी-ध्वनि होती है।
डिजाइन संरचना मैट्रिक्स (डीएसएम) प्रक्रिया संबंधों को मॉडल कर सकता है, और प्रक्रिया नियोजन के लिए उपयोग किया जा सकता है। डीएसएम-नेट, पेट्री नेट द्वारा कार्यप्रवाह प्रक्रियाओं में डीएसएम-आधारित योजनाओं की प्राप्ति करता है, और डब्ल्यूआरआई-डब्ल्यूएफ-नेट के समकक्ष होता है। डीएसएम-नेट निर्माण प्रक्रिया परिणामी नेट की सुदृढ़ता संपत्ति सुनिश्चित करता है।
समवर्ती के अन्य मॉडल
मॉडलिंग समवर्ती संगणना के अन्य विधियों का प्रस्ताव किया गया है, जिसमें वेक्टर जोड़ प्रणाली, परिमित-राज्य मशीनों का संचार, क्हान प्रक्रिया नेटवर्क, प्रक्रिया बीजगणित, अभिनेता मॉडल और ट्रेस सिद्धांत सम्मलित है।[27] विभिन्न मॉडल संरचना, प्रतिरूपकता (प्रोग्रामिंग) और स्थानीयता जैसी अवधारणाओं का व्यापार प्रदान करते है।
विन्सेल और नीलसन द्वारा अध्याय में समवर्ती के इन मॉडलों में से कुछ को संबंधित करने का एक दृष्टिकोण प्रस्तावित है।[28]
उपयेाग क्षेत्र
- कम्प्यूटेशनल बायोलॉजी[31][32]
- समवर्ती प्रोग्रामिंग[33]
- नियंत्रण इंजीनियरिंग[15][34][35]
- डेटा विश्लेषण[36]
- निदान (कृत्रिम बुद्धि)[37]
- डायग्नोसिस (आर्टिफिशियल इंटेलिजेंस)[38]
- अनुक्रमिक फ़ंक्शन चार्ट[39][40]
- खेल सिद्धांत[41]
- सिग्नल संक्रमण रेखांकन[42][43][44]
- क्हान प्रक्रिया नेटवर्क[45]
- प्रक्रिया मॉडलिंग[46][47][48]
- स्थिरता अभियांत्रिकी[49]
- सिमुलेशन[50]* सॉफ्टवेर डिज़ाइन[14]
- वर्कफ़्लो प्रबंधन प्रणाली[51][47][48]
यह भी देखें
- परिमित अवस्था मशीन
- पेट्री नेट मार्कअप लैंग्वेज
- पेट्रीस्क्रिप्ट
- प्रक्रिया संरचना
- वेक्टर जोड़ प्रणाली
- यंत्र अधिगम
संदर्भ
- ↑ Petri, Carl Adam; Reisig, Wolfgang (2008). "पेट्री नेट". Scholarpedia. 3 (4): 6477. Bibcode:2008SchpJ...3.6477P. doi:10.4249/scholarpedia.6477.
- ↑ Rozenburg, G.; Engelfriet, J. (1998). "Elementary Net Systems". In Reisig, W.; Rozenberg, G. (eds.). Lectures on Petri Nets I: Basic Models – Advances in Petri Nets. Lecture Notes in Computer Science. Vol. 1491. Springer. pp. 12–121.
- ↑ Reisig, Wolfgang (1991). "पेट्री नेट और बीजगणितीय विनिर्देश". Theoretical Computer Science. 80 (1): 1–34. doi:10.1016/0304-3975(91)90203-e.
- ↑ Desel, Jörg; Juhás, Gabriel (2001). "What Is a Petri Net? Informal Answers for the Informed Reader". In Ehrig, Hartmut; et al. (eds.). पेट्री नेट्स को एकीकृत करना. LNCS. Vol. 2128. Springer. pp. 1–25. doi:10.1007/3-540-45541-8_1. ISBN 9783540430674.
- ↑ Meseguer, Jose; Montanari, Ugo (October 1990). "Petri nets are monoids". Information and Computation. 88 (2): 105–155. doi:10.1016/0890-5401(90)90013-8. Retrieved 30 December 2022.
- ↑ Esparza, Javier; Nielsen, Mogens (1995) [1994]. "Decidability issues for Petri nets – a survey". Bulletin of the EATCS (Revised ed.). Retrieved 2014-05-14.
- ↑ Lipton, R. (1976). "रीचैबिलिटी प्रॉब्लम के लिए एक्सपोनेंशियल स्पेस की आवश्यकता होती है". Technical Report 62.
- ↑ Küngas, P. (July 26–29, 2005). पेट्री नेट रीचैबिलिटी चेकिंग इज पोलीनॉमियल विथ ऑप्टिमल एब्सट्रैक्शन हायरार्कीज. Proceedings of the 6th International Symposium on Abstraction, Reformulation and Approximation—SARA 2005. Airth Castle, Scotland, UK. Archived from the original on 9 February 2012. Retrieved 10 July 2008.
- ↑ Czerwiński, Wojciech; Lasota, Sławomir; Lazic, Ranko; Leroux, Jerome; Mazowiecki, Filip (2018). "पेट्री नेट्स के लिए रीचैबिलिटी की समस्या प्राथमिक नहीं है (विस्तारित सार)". arXiv:1809.07115 [cs.FL].
- ↑ Leroux, Jérôme (2021). "पेट्री नेट्स के लिए रीचैबिलिटी प्रॉब्लम प्रिमिटिव रिकर्सिव नहीं है". arXiv:2104.12695 [cs.LO].
- ↑ Czerwiński, Wojciech; Orlikowski, Łukasz (2021). "सदिश जोड़ प्रणालियों में पहुंच क्षमता एकरमैन-पूर्ण है". arXiv:2104.13866 [cs.FL].
- ↑ Murata, Tadao (April 1989). "Petri Nets: Properties, Analysis and Applications". Proceedings of the IEEE. 77 (4): 541–558. doi:10.1109/5.24143. Retrieved 2014-10-13.
- ↑ "Petri Nets". www.techfak.uni-bielefeld.de.
- ↑ 14.0 14.1 Kučera, Erik; Haffner, Oto; Drahoš, Peter; Cigánek, Ján; Leskovský, Roman; Štefanovič, Juraj (January 2020). "टाइम्ड इंटरप्रिटेड पेट्री नेट्स का उपयोग करके डिस्क्रीट-इवेंट और हाइब्रिड सिस्टम के मॉडलिंग और नियंत्रण के लिए नया सॉफ्टवेयर टूल". Applied Sciences (in English). 10 (15): 5027. doi:10.3390/app10155027.
- ↑ 15.0 15.1 David, René; Alla, Hassane (2005). असतत, निरंतर और हाइब्रिड पेट्री नेट्स. Springer. ISBN 978-3-540-22480-8.
- ↑ Jensen, Kurt (1997). "A brief introduction to coloured Petri Nets" (PDF). रंगीन पेट्री जालों का संक्षिप्त परिचय. Lecture Notes in Computer Science. Vol. 1217. pp. 203–208. doi:10.1007/BFb0035389. ISBN 978-3-540-62790-6.
- ↑ Araki, T.; Kasami, T. (1977). "पेट्री नेट्स के लिए रीचैबिलिटी प्रॉब्लम से संबंधित कुछ निर्णय समस्याएं". Theoretical Computer Science. 3 (1): 85–104. doi:10.1016/0304-3975(76)90067-0.
- ↑ Dufourd, C.; Finkel, A.; Schnoebelen, Ph. (1998). "Reset Nets Between Decidability and Undecidability". Proceedings of the 25th International Colloquium on Automata, Languages and Programming. LNCS. Vol. 1443. pp. 103–115.
- ↑ Zaitsev, D. A. (2013). "मिनिमल यूनिवर्सल पेट्री नेट की ओर". IEEE Transactions on Systems, Man, and Cybernetics: Systems. 44: 47–58. doi:10.1109/TSMC.2012.2237549. S2CID 6561556.
- ↑ "सीपी-नेट का बहुत संक्षिप्त परिचय". Department of Computer Science, University of Aarhus, Denmark.
- ↑ "LLPN - रैखिक तर्क पेट्री नेट". Archived from the original on 2005-11-03. Retrieved 2006-01-06.
- ↑ Dawis, E. P.; Dawis, J. F.; Koo, Wei-Pin (2001). द्वैतवादी पेट्री नेट का उपयोग करते हुए कंप्यूटर आधारित प्रणालियों की वास्तुकला. 2001 IEEE International Conference on Systems, Man, and Cybernetics. Vol. 3. pp. 1554–1558.
- ↑ Dawis, E. P. (2001). Architecture of an SS7 Protocol Stack on a Broadband Switch Platform using Dualistic Petri Nets. 2001 IEEE Pacific Rim Conference on Communications, Computers and signal Processing. Vol. 1. pp. 323–326.
- ↑ 24.0 24.1 24.2 van der Aalst, W. M. P. (1998). "वर्कफ़्लो प्रबंधन के लिए पेट्री नेट का अनुप्रयोग" (PDF). Journal of Circuits, Systems and Computers. 8 (1): 21–66. CiteSeerX 10.1.1.30.3125. doi:10.1142/s0218126698000043. S2CID 248401501.
- ↑ van Hee, K.; Sidorova, N.; Voorhoeve, M. (2003). "Soundness and separability of workflow nets in the stepwise refinement approach" (PDF). In van der Aalst, W. M. P.; Best, E. (eds.). Application and Theory of Petri Nets 2003. Lect Notes in Comput Sci. Vol. 2678. Springer. pp. 337–356.
- ↑ 26.0 26.1 Ping, L.; Hao, H.; Jian, L. (2004). Moldt, Daniel (ed.). वर्कफ्लो नेट की 1-सुदृढ़ता और सुदृढ़ता पर. Proc of the 3rd Workshop on Modelling of Objects, Components, and Agents. Vol. 571. Aarhus, Denmark: DAIMI PB. pp. 21–36.
- ↑ Mazurkiewicz, Antoni (1995). "Introduction to Trace Theory". In Diekert, V.; Rozenberg, G. (eds.). निशान की किताब. Singapore: World Scientific. pp. 3–67.
- ↑ Winskel, G.; Nielsen, M. "Models for Concurrency" (PDF). हैंडबुक ऑफ़ लॉजिक एंड द फ़ाउंडेशन ऑफ़ कंप्यूटर साइंस. Vol. 4. OUP. pp. 1–148. Archived from the original (PDF) on 4 May 2020.
- ↑ Scheuring, Rainer; Wehlan, Herbert "Hans" (1991-12-01) [July 1991]. Bretthauer, Georg (ed.). "बूलियन डिफरेंशियल कैलकुलस - पेट्री नेट के विश्लेषण और संश्लेषण के लिए एक विधि" [The Boolean differential calculus – A method for analysis and synthesis of Petri nets]. At – Automatisierungstechnik – Methoden und Anwendungen der Steuerungs-, Regelungs- und Informationstechnik (in Deutsch). Stuttgart, Germany: R. Oldenbourg Verlag. 39 (7): 226–233. doi:10.1524/auto.1991.39.112.226. ISSN 0178-2312. S2CID 56766796. Archived from the original on 2017-10-16. Retrieved 2017-10-16. (8 पृष्ठ)
- ↑ van der Aalst, W.M.P. (2018). "Business Process Management". डेटाबेस सिस्टम्स का विश्वकोश, दूसरा संस्करण. Springer. pp. 370–374. doi:10.1007/978-1-4614-8265-9_1179. ISBN 978-1-4614-8266-6.
- ↑ Favrin, Bean (2 September 2014). "esyN: Network Building, Sharing and Publishing". PLOS ONE. 9 (9): e106035. Bibcode:2014PLoSO...9j6035B. doi:10.1371/journal.pone.0106035. PMC 4152123. PMID 25181461.
- ↑ Koch, Ina; Reisig, Wolfgang; Schreiber, Falk (2011). सिस्टम बायोलॉजी में मॉडलिंग - पेट्री नेट दृष्टिकोण. Computational Biology. Vol. 16. Springer. doi:10.1007/978-1-84996-474-6. ISBN 978-1-84996-473-9.
- ↑ Kristensen, L. M.; Westergaard, M. (2010). "Automatic Structure-Based Code Generation from Coloured Petri Nets: A Proof of Concept". औद्योगिक महत्वपूर्ण प्रणालियों के लिए औपचारिक तरीके. औद्योगिक महत्वपूर्ण प्रणालियों के लिए औपचारिक तरीके- 15th International Workshop, FMICS 2010. Lecture Notes in Computer Science. Vol. 6371. pp. 215–230. doi:10.1007/978-3-642-15898-8_14. ISBN 978-3-642-15897-1.
- ↑ Gao, X.; Hu, Xinyan (2020). "नए पेस्ट बैकफिल प्रोसेस मॉडल के लिए एक पेट्री नेट न्यूरल नेटवर्क मजबूत नियंत्रण". IEEE Access. 8: 18420–18425. doi:10.1109/ACCESS.2020.2968510. S2CID 210994447.
- ↑ Kučera, Erik; Haffner, Oto; Drahoš, Peter; Leskovský, Roman; Cigánek, Ján (January 2020). "PetriNet Editor + PetriNet Engine: New Software Tool For Modelling and Control of Discrete Event Systems Using Petri Nets and Code Generation". Applied Sciences (in English). 10 (21): 7662. doi:10.3390/app10217662.
- ↑ van der Aalst, W.M.P. (2016). प्रोसेस माइनिंग - डेटा साइंस इन एक्शन, दूसरा संस्करण. Springer. doi:10.1007/978-3-662-49851-4. ISBN 978-3-662-49850-7. S2CID 12806779.
- ↑ Carmona, J.; van Dongen, B.F.; Solti, A.; Weidlich, M. (2018). अनुरूपता जाँच - प्रक्रियाओं और मॉडलों से संबंधित. Springer. doi:10.1007/978-3-319-99414-7. ISBN 978-3-319-99413-0. S2CID 53250018.
- ↑ Fernandez, J. L.; Sanz, R.; Paz, E.; Alonso, C. (19–23 May 2008). "Using hierarchical binary Petri nets to build robust mobile robot applications: RoboGraph". IEEE International Conference on Robotics and Automation, 2008. Pasadena, CA, USA. pp. 1372–1377. doi:10.1109/ROBOT.2008.4543394. ISBN 978-1-4244-1646-2.
- ↑ Mendes, J. Marco; Leitão, Paulo; Colombo, Armando W.; Restivo, Francisco (2012). "सेवा-उन्मुख निर्माण प्रणालियों में प्रक्रिया विवरण और नियंत्रण के लिए उच्च-स्तरीय पेट्री नेट". International Journal of Production Research. Taylor & Francis. 50 (6): 1650–1665. doi:10.1080/00207543.2011.575892. S2CID 39688855.
- ↑ Fahland, D.; Gierds, C. (2013). "Analyzing and Completing Middleware Designs for Enterprise Integration Using Coloured Petri Nets". Active Flow and Combustion Control 2018. Advanced Information Systems Engineering - 25th International Conference, CAiSE 2013. Lecture Notes in Computer Science. Vol. 7908. pp. 400–416. doi:10.1007/978-3-642-38709-8_26. ISBN 978-3-319-98176-5.
- ↑ Clempner, Julio (2006). "Modeling shortest path games with Petri nets: a Lyapunov based theory". International Journal of Applied Mathematics and Computer Science (in English). 16 (3): 387–397. ISSN 1641-876X.
- ↑ Yakovlev, Alex; Gomes, Luis; Lavagno, Luciano, eds. (2000). हार्डवेयर डिजाइन और पेट्री नेट (in British English). doi:10.1007/978-1-4757-3143-9. ISBN 978-1-4419-4969-1.
- ↑ Cortadella, J.; Kishinevsky, M.; Kondratyev, A.; Lavagno, L.; Yakovlev, A. (2002). "अतुल्यकालिक नियंत्रकों और इंटरफेस के लिए तर्क संश्लेषण". Springer Series in Advanced Microelectronics (in British English). 8. doi:10.1007/978-3-642-55989-1. ISBN 978-3-642-62776-7. ISSN 1437-0387.
- ↑ Cortadella, Jordi; Yakovlev, Alex; Rozenberg, Grzegorz, eds. (2002). "संगामिति और हार्डवेयर डिजाइन". Lecture Notes in Computer Science (in British English). 2549. doi:10.1007/3-540-36190-1. ISBN 978-3-540-00199-7. ISSN 0302-9743. S2CID 42026227.
- ↑ Bernardeschi, C.; De Francesco, N.; Vaglini, G. (1995). "डेटा प्रवाह नेटवर्क के लिए एक पेट्री नेट सिमेंटिक्स". Acta Informatica. 32 (4): 347–374. doi:10.1007/BF01178383. S2CID 7285573.
- ↑ van der Aalst, Wil M. P.; Stahl, Christian; Westergaard, Michael (2013). "रंगीन पेट्री नेट का उपयोग करके मॉडलिंग जटिल प्रक्रियाओं के लिए रणनीतियाँ". Trans. Petri Nets Other Model. Concurr. Lecture Notes in Computer Science. 7: 6–55. doi:10.1007/978-3-642-38143-0_2. ISBN 978-3-642-38142-3.
- ↑ 47.0 47.1 van der Aalst, W.M.P. (2018). "Workflow Patterns". डेटाबेस सिस्टम्स का विश्वकोश, दूसरा संस्करण. Springer. pp. 4717–4718. doi:10.1007/978-1-4614-8265-9_826. ISBN 978-1-4614-8266-6.
- ↑ 48.0 48.1 van der Aalst, W.M.P. (2018). "Workflow Model Analysis". डेटाबेस सिस्टम्स का विश्वकोश, दूसरा संस्करण. Springer. pp. 4716–4717. doi:10.1007/978-1-4614-8265-9_1476. ISBN 978-1-4614-8266-6.
- ↑ O'Connor, Patrick D. T. (2012). व्यावहारिक विश्वसनीयता इंजीनियरिंग. Andre Kleyner (5th ed.). Chichester, West Sussex, U.K.: Wiley. ISBN 978-1-119-96126-0. OCLC 862121371.
- ↑ Cite error: Invalid
<ref>tag; no text was provided for refs namedAalstStahl2011 - ↑ ter Hofstede, Arthur H. M.; van der Aalst, Wil M. P.; Adams, Michael; Russell, Nick (2010). Hofstede, Arthur H. M; Aalst, Wil M. P; Adams, Michael; Russell, Nick (eds.). आधुनिक व्यवसाय प्रक्रिया स्वचालन - YAWL और इसका समर्थन पर्यावरण. doi:10.1007/978-3-642-03121-2. ISBN 978-3-642-03122-9.
अग्रिम पठन
- Cardoso, Janette; Camargo, Heloisa (1999). Fuzziness in Petri Nets. Physica-Verlag. ISBN 978-3-7908-1158-2.
- Chiachio, Manuel; Chiachio, Juan; Presscott, Darren; Andrews, John (2018). "A new paradigm for uncertain knowledge representation by 'Plausible Petri nets'". Information Sciences. 453 (July 2018): 323–345. doi:10.1016/j.ins.2018.04.029.
- Grobelna, Iwona (2011). "Formal verification of embedded logic controller specification with computer deduction in temporal logic". Przegląd Elektrotechniczny. 87 (12a): 47–50.
- Jensen, Kurt (1997). Coloured Petri Nets. Springer Verlag. ISBN 978-3-540-62867-5.
- Pataricza, András (2004). Formális módszerek az informatikában (Formal methods in informatics). TYPOTEX Kiadó. ISBN 978-963-9548-08-4.
- Peterson, James Lyle (1977). "Petri Nets". ACM Computing Surveys. 9 (3): 223–252. doi:10.1145/356698.356702. hdl:10338.dmlcz/135597. S2CID 3605804.
- Peterson, James Lyle (1981). Petri Net Theory and the Modeling of Systems. Prentice Hall. ISBN 978-0-13-661983-3.
- Petri, Carl Adam (1962). Kommunikation mit Automaten (Ph. D. thesis). University of Bonn.
- Petri, Carl Adam; Reisig, Wolfgang (2008). "Petri net". Scholarpedia. 3 (4): 6477. Bibcode:2008SchpJ...3.6477P. doi:10.4249/scholarpedia.6477.
- Reisig, Wolfgang (1992). A Primer in Petri Net Design. Springer-Verlag. ISBN 978-3-540-52044-3.
- Riemann, Robert-Christoph (1999). Modelling of Concurrent Systems: Structural and Semantical Methods in the High Level Petri Net Calculus. Herbert Utz Verlag. ISBN 978-3-89675-629-9.
- Störrle, Harald (2000). Models of Software Architecture – Design and Analysis with UML and Petri-Nets. Books on Demand. ISBN 978-3-8311-1330-9.
- Zaitsev, Dmitry (2013). Clans of Petri Nets: Verification of protocols and performance evaluation of networks. LAP LAMBERT Academic Publishing. ISBN 978-3-659-42228-7.
- Zhou, Mengchu; Dicesare, Frank (1993). Petri Net Synthesis for Discrete Event Control of Manufacturing Systems. Kluwer Academic Publishers. ISBN 978-0-7923-9289-7.
- Zhou, Mengchu; Venkatesh, Kurapati (1998). Modeling, Simulation, & Control of Flexible Manufacturing Systems: A Petri Net Approach. World Scientific Publishing. ISBN 978-981-02-3029-6.